2018年（平成30年）度に福岡県で行われた公立高校入試の数学第4問の解説です。
問4は1次関数の問題で条件が日本語でずらずら書かれていてとっつきにくいですが、
ルールさえ知ってしまえば簡単な1次関数の交点問題です。
問題は福岡県の公式サイトにもあります。
\(\large{\color{black}{\fbox{ 4 }}}\)
この問題は小学生でも解けそうで、解説をつけるほどの問題ではないのでパスしてもよかったのですが、こういう長い文章題が苦手な人が余りにも多すぎるので解説しておきます。
この問題、日本文から「水そう」という文字をとってしまうとすっきりしませんか？
ついでに「管」というのもなくしておきます。
ということで
「水そう\(\,\mathrm{A}\,\)」を単に\(\,\mathrm{A}\,\)
と表すようにします。同様に、
「水そう\(\,\mathrm{B}\,\)」を\(\,\mathrm{B}\,\)
「\(\,\mathrm{P}\,\)管」を\(\,\mathrm{P}\,\)
「\(\,\mathrm{Q}\,\)管」を\(\,\mathrm{Q}\,\)
「\(\,\mathrm{R}\,\)管」を\(\,\mathrm{R}\,\)
と表します。
書いてある条件を整理しましょう。
\(\,\mathrm{P}\,\)と\(\,\mathrm{Q}\,\)を使って\(\,\mathrm{A}\,\)に水を入れる。
\(\,\mathrm{R}\,\)を使って\(\,\mathrm{B}\,\)に水を入れる。
\(\,\mathrm{P,Q,R}\,\)はそれぞれ一定の量の水が出る。
\(\,\mathrm{P}\,\)だけだと毎分\(\,2\mathrm{cm}\,\)ずつ高くなる。
\(\,\mathrm{P}\,\)だけ\(\,5\,\)分、\(\,\mathrm{(P+Q)}\,\)で\(\,4\,\)分、\(\,\mathrm{P}\,\)だけ\(\,6\,\)分入れると\(\,39\mathrm{cm}\,\)。
水を入れた時間と\(\,\mathrm{A}\,\)の水の高さを表したのが\(\,図2\,\)です。
（\(\,図1\,\)は日本語で読み取れない人へのヒントでしょうか？必要ありません。）
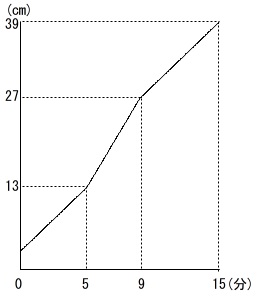このグラフは、
①\(\,\mathrm{P}\,\)だけで\(\,5\,\)分
②\(\,\mathrm{P+Q}\,\)で\(\,4\,\)分
③再び\(\,\mathrm{P}\,\)だけで\(\,6\,\)分
水を入れた高さの変化です。
気がつかなければならないのは、\(\,\mathrm{P}\,\)はずっと入れっぱなしだということですね。
違っているのは②の段階だけなのでここがポイントになりそうです。
すべての関数を出しておきたいところですが、誘導に乗りましょうか。
（すべての関数を出しておけば最後までノンストップで終わります。）
(1)\(\,\mathrm{A}\,\)に水を入れはじめてから\(\,3\,\)分後までの水面までの高さの関係を正しく表しているものを選びます。
グラフを見ると、\(\,5\,\)分後は\(\,13\mathrm{cm}\,\)になっています。
このア～エの表が\(\,3\,\)分までしかないことを見て下さい。
\(\,5\,\)分まであれば答えが分かるから書いていないのです。笑
続きを書いてみましょう。
高さは一定の割合で増えます。
ア：\(\,1\,\)分で\(\,1\mathrm{cm}\,\)ずつ増える。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
時間 & 0 & 1 & 2 & 3 & 4 & \color{red}{5} \\ \hline
高さ & 3 & 4 & 5 & 6 & 7 & \color{red}{8} \\ \hline
\end{array}\)
イ：\(\,1\,\)分で\(\,2\mathrm{cm}\,\)ずつ増える。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
時間 & 0 & 1 & 2 & 3 & 4 & \color{red}{5} \\ \hline
高さ & 3 & 5 & 7 & 9 & 11 & \color{red}{13} \\ \hline
\end{array}\)
ウ：\(\,1\,\)分で\(\,1\mathrm{cm}\,\)ずつ増える。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
時間 & 0 & 1 & 2 & 3 & 4 & \color{red}{5} \\ \hline
高さ & 5 & 6 & 7 & 8 & 9 & \color{red}{10} \\ \hline
\end{array}\)
エ：\(\,1\,\)分で\(\,2\mathrm{cm}\,\)ずつ増える。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
時間 & 0 & 1 & 2 & 3 & 4 & \color{red}{5} \\ \hline
高さ& 5 & 7 & 9 & 11 & 13 & \color{red}{15} \\ \hline
\end{array}\)
この中で\(\,5\,\)分で\(\,13\mathrm{cm}\,\)になっているのは、
（答え） \(\,\underline{ イ }\,\)
問題に\(\,5\,\)分で\(\,13\mathrm{cm}\,\)になっている、と書いてあるんですよ。
(2)\(\,\mathrm{Q}\,\)だけで水を入れると毎分何\(\,\mathrm{cm}\,\)あがるか？
グラフを見ればわかりますが、
\(\,\mathrm{P}\,\)と\(\,\mathrm{Q}\,\)両方使って入れると\(\,4\,\)分間で
\(27-13=14\,\mathrm{cm}\)
\(\,\mathrm{P}\,\)は\(\,1\,\)分間で\(\,2\mathrm{cm}\,\)あがるというのは(1)で分かっているので\(\,4\,\)分間で
\(2\times 4=8\,\mathrm{cm}\)
ということは\(\,\mathrm{Q}\,\)が上げた高さは\(\,4\,\)分間で
\(14-8=6\,\mathrm{cm}\)
ということなので、毎分
\(\displaystyle \frac{6}{4}=\underline{ \frac{3}{2}\,\mathrm{(cm)} }\)
ずつ高くなる。
これをグラフで見ると
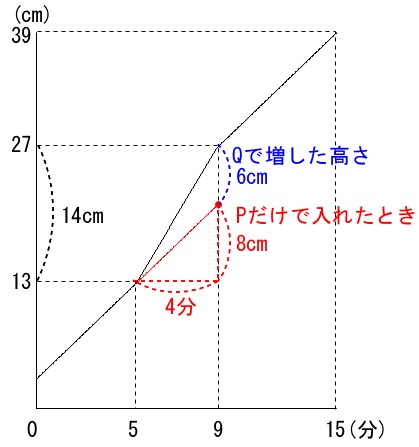ということです。
関数で出した方が確実ですけど、グラフを利用した方が簡単です。
(3)でようやく\(\,\mathrm{B}\,\)が登場します。
\(\,30\,\mathrm{cm}\,\)まで水は入っている。
\(\,\mathrm{A}\,\)に遅れて\(\,9\,\)分後に水を\(\,\mathrm{R}\,\)で入れはじめる。
\(\,6\,\)分後に高さが\(\,38\,\mathrm{cm}\,\)になった。
これが\(\,\mathrm{B}\,\)と\(\,\mathrm{R}\,\)についての条件です。
\(\,\mathrm{B}\,\)の水面の高さをグラフにすると、\(\,\mathrm{A}\,\)を入れはじめた時点を\(\,0\,\)分とすると
\(\,9\,\)分後\(\,30\,\mathrm{cm}\,\)
\(\,15\,\)分後に\(\,38\,\mathrm{cm}\,\)
なので\(\,図2\,\)に重ねると
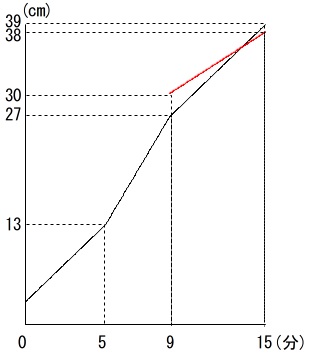図の赤線になります。
同じ高さになるのは\(\,\mathrm{A}\,\)のグラフと\(\,\mathrm{B}\,\)のグラフの交点の座標が分かれば良いのですが、正確に読み取るには関数として処理するしかないですね。
勘、というのも良いですけどこの問題は理由が必要です。笑
これを関数の交点問題と置きかえればものすごく簡単な\(\,1\,\)次関数の交点問題です。
\(\,\mathrm{A}\,\)に水を入れてからの時間を\(\,x\,\)、水の高さを\(\,y\,\)とする
と問題に書いてあるのでこの\(\,(x,y)\,\)の関数を\(\,\mathrm{A}\,\)、\(\,\mathrm{B}\,\)それぞれ出せば終わります。
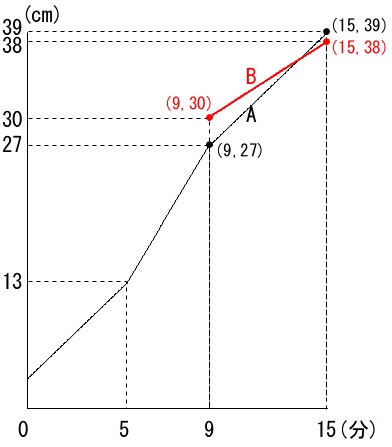
\(9\,≦\,x\,≦\,15\,\)における\(\,\mathrm{A}\,\)の関数は、
\(\,2\,\)点\(\,(\,9\,,\,27\,),(\,15\,,\,39\,)\,\)を通るので
\(\begin{eqnarray}
(傾き)&=&\displaystyle \frac{39-27}{15-9}\\
&=&\frac{12}{6}\\
&=&2
\end{eqnarray}\)
で\(\,(\,9\,,\,27\,),(\,15\,,\,39\,)\,\)のどちらかを通ることから
\(\begin{eqnarray}
y&=&2x+b\\
27&=&2\times (9)+b\\
27&=&18+b\\
27-18&=&b\\
9&=&b
\end{eqnarray}\)
よって\(\,9\,≦\,x\,≦\,15\,\)における\(\,\mathrm{A}\,\)の関数は
\(y=2x+9 ･･･①\)
もちろん\(\,(\,15\,,\,39\,)\,\)を代入しても成り立たないといけません。
また
\(9\,≦\,x\,≦\,15\,\)における\(\,\mathrm{B}\,\)の関数は、
\(\,2\,\)点\(\,(\,9\,,\,30\,),(\,15\,,\,38\,)\,\)を通るので
\(\begin{eqnarray}
(傾き)&=&\displaystyle \frac{38-30}{15-9}\\
&=&\frac{8}{6}\\
&=&\frac{4}{3}
\end{eqnarray}\)
で\(\,(\,9\,,\,30\,),(\,15\,,\,38\,)\,\)のどちらかを通ることから
\(\begin{eqnarray} \displaystyle
y&=&\frac{4}{3}x+b\\
30&=&\frac{4}{3}\times (9)+b\\
30&=&12+b\\
30-12&=&b\\
18&=&b
\end{eqnarray}\)
よって\(\,9\,≦\,x\,≦\,15\,\)における\(\,\mathrm{B}\,\)の関数は
\(\displaystyle y=\frac{4}{3}x+18 ･･･②\)
これも代入していないもう一つの点\(\,(\,15\,,\,38\,)\,\)を代入しても成り立たなくてはいけません。
①②の交点は連立すれば良いだけです。
『交点』と見つけたら『連立』
これは高校の数学でも同じです。
①②を連立すると
\( \begin{cases}
\hspace{7pt} y=2x+9\\ \\
\hspace{7pt}\displaystyle y=\frac{4}{3}x+18
\end{cases}\)
左辺が同じだから右辺どうしも等しいので
\(\begin{eqnarray}\displaystyle
2x+9&=&\frac{4}{3}x+18\\
6x+27&=&4x+54\\
6x-4x&=&54-27\\
2x&=&27\\
x&=&\frac{27}{2} （9≦x≦15に適。）
\end{eqnarray}\)
この\(\,x\,\)は\(\,\mathrm{A}\,\)に水を入れはじめてからの時間なので
\(\displaystyle \frac{27}{2}=13+\frac{1}{2} (分)\)
答えは\(\color{black}{\fbox{ 13 分 30 秒後 }}\)
「理由は簡潔に書くこと」、とあるので
2つの直線が上で示した\(\,2\,\)点を通り
\(\,y=2x+9\,\)
\(\,\displaystyle y=\frac{4}{3}x+18\,\)
であることと、
交点で同じ高さになること
を書いておけば良いでしょう。
福岡県の解答には\(\,y\,\)座標が求めてあるらしいけど、問題に求められてはいません。
私は見ていませんでした。
減点されても高々\(\,1\,\)点か\(\,2\,\)点でしょう？
実際の試験では時間あまりまくるだろうから書くだろうけど、それほど気にすることでもありません。
気にするとしたら何を聞かれているかの確認だし、普通の受験生には他の問題の見直しをおすすめします。
\(\large{\color{black}{\fbox{ 4 }}}\)はたったこれだけです。
⇒ 2018年福岡県公立高校入試 数学問5の平面図形問題の解説
次は平面図形で、円の性質と相似から面積計算まであります。
少しだけ高校入試らしい数字が出てきますが、でっかい覚悟が必要になるほどのものでもありません。
⇒ 福岡県公立高校入試問題2018(平成30年度)の数学の過去問解説
図形が超苦手なら問1からの見直し優先ですよ。
『覚え太郎』は図形が大の得意分野です。
毎年この時期（これ書いているのはセンター試験当日です。ｗ）からでも急激に伸びる受験生たくさんいます。
何度でもいいますが、やり方間違わなければ中学生はひと月あれば数学の成績化けますよ。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
