2018年(平成30年)度に福岡県で行われた公立高校入試の数学(問5の平面図形)問題の解説です。
合同は証明してくれていて、相似の証明がありますけど誘導がきっちりされています。
面積計算がありますが、図を問題ごとにわざわざつけてくれているので取り組みやすかったのではないでしょうか。
問題は福岡県の公式サイトにもあります。
合同の証明が終わった後
図形問題では合同の証明か相似の証明がよくありますが、
証明したことを利用して後の問題を解決するように誘導されることが普通です。
証明が問題になりますが、証明自体が本題では無いということです。
証明した事実を利用する、これは普通のことなので忘れないようにしましょう。
ただ、ここでは合同を証明してくれています。
しかも、合同だからいえることまでも1つ教えてくれています。
合同が言えると他に何が言えるか、それがこの問題(1)です。
(1)本当なら証明は自分でするので証明する前に終わっているはずなのですが、
分かることを図に書き込んでおきます。
問題にある条件は
\(\,\mathrm{\color{blue}{BC=6}}\,\)
\(\,\mathrm{\color{red}{AC=DB}}\,\)
\(\,\mathrm{\color{red}{∠ACB=∠DBC}}\,\)

さらに
\(\,\mathrm{\color{magenta}{△ABC ≡ △DCB}}\,\)
が言えることから
\(\,\mathrm{\color{blue}{∠BAC=∠CDB}}\,\)
も証明してくれています。
では合同なら何が言えるか?
「対応するすべての辺と角が等しい。」
ですよね。
\(\,\mathrm{△ABC ≡ △DCB}\,\)
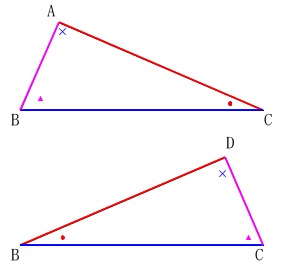 なので、
なので、
\(\,\mathrm{\color{magenta}{AB=DC}}\,\)
\(\,\mathrm{\color{blue}{BC=CB}}\,(済み)\)
\(\,\mathrm{\color{red}{AC=DB}}\,(済み)\)
\(\,\mathrm{\color{blue}{∠BAC=∠CDB}}\,(済み)\)
\(\,\mathrm{\color{magenta}{∠ABC=∠DCB}}\,\)
\(\,\mathrm{\color{red}{∠ACB=∠DBC}}\,(済み)\)
この中でまだいっていないのは、
\(\,\mathrm{\underline{ AB=DC }}\,\)
\(\,\mathrm{\underline{ ∠ABC=∠DCB }}\,\)
記号が打ってないので書きませんが二等辺三角形も出てきているので、言えることはもっと増えます。
ここで時間をかけても仕方ないので次に行きます。
相似の証明
(2)は相似を証明します。
\(\,図2\,\)は\(\,図1\,\)の条件を持っていますよ。
(1)の前にある条件は問題のすべてに共通する条件です。
\(\,図1\,\)に(2)の条件を加えます。
\(\,\mathrm{BC}\,\)を直径とする円の中心が\(\,\mathrm{O}\,\)
\(\,\mathrm{AC}\,\)と\(\,\mathrm{BD}\,\)の交点を\(\,\mathrm{E}\,\)
\(\,\mathrm{AC}\,\)と\(\,\mathrm{OD}\,\)の交点を\(\,\mathrm{F}\,\)
言えることはたくさん出てきますが、証明に使う部分だけを図で示します。
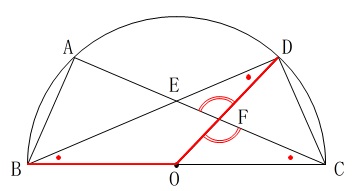 (1)の合同から
(1)の合同から
\(\,\mathrm{∠ACB=∠DBC}\, ・・・①\)
また、円の半径は常に等しいので
\(\,\mathrm{△OBD}\,\)は二等辺三角形
なので
\(\,\mathrm{∠OBD=∠ODB}\, ・・・②\)
①②から
\(\,\mathrm{∠OCF=∠EDF}\, ・・・③\)
対頂角は等しいから
\(\,\mathrm{∠OFC=∠EFD}\, ・・・④\)
③④から\(\,2\,\)角相等条件(\(\,2\,\)組の角がそれぞれ等しい)がそろうので
\(\,\mathrm{△OCF}\) ∽ \(\mathrm{△EDF}\,\)
証明は適当に書いておいて下さい。笑
等しい\(\,2\,\)組の角を書いて、
半径で作る二等辺三角形
のことが書かれていれば減点対象もないでしょう。
この段階で\(\,\mathrm{E,F}\,\)がつけられたので言えることは山ほど出てきますが、
全部書いていたら時間をムダにするので(3)に進み、必要な部分を書き込んでいきましょう。
ただ、使うかどうかは分かりませんが、1つか2つは利用できるくらいの検討をつけておいた方が良いですよ。
その問題が解ければ良い、みたいなケチくさいこといわず、何を誘導してくれているのかくらい普段から見ておくようにしましょう。
そうすることで\(\,1\,\)問\(\,1\,\)問が大きな価値を持ってくるのです。
入試のときはその問題が解けなければ意味がないので、その問題さえ解ければ良いです。
普段の練習の話です。
条件は必要だから与えてくれている
(3)
「\(\,図2\,\)において」ということは\(\,図3\,\)に与えられる条件は今までのすべてです。
これを見落とすと誘導される問題は解けません。
この問題は誘導されたことを図示するとものすごく簡単です。
ただし、面積を比を利用して求める教科書レベルの基本ができていないと意味がありません。
入試問題は基本の組み合わせです。
基本中心の対策を忘れないようにしましょう。
(3)の条件を図示します。
条件は(2)までのすべてと、
\( \color{red}{\stackrel{\Large{\frown}}{\mbox{AB}}\,=\,\stackrel{\Large{\frown}}{\mbox{AD}} }\)
\(\,\mathrm{CD}\,\)の中点を\(\,\mathrm{G}\,\)
\(\,\mathrm{BG}\,\)と\(\,\mathrm{OD}\,\)の交点を\(\,\mathrm{H}\,\)
\(\,\mathrm{GI}\,\)は\(\,\mathrm{AB}\,\)に平行
これを図示しますが、見落としてはならないのが
\( \color{red}{\stackrel{\Large{\frown}}{\mbox{AB}}\,=\,\stackrel{\Large{\frown}}{\mbox{AD}} }\)
です。
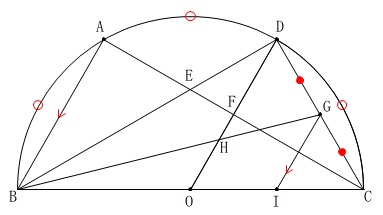
もともと\(\,\mathrm{AB=DC}\,\)なので
\( \color{red}{\stackrel{\Large{\frown}}{\mbox{AB}}\,=\,\stackrel{\Large{\frown}}{\mbox{DC}} }\)
が言えており、
\( \color{blue}{\stackrel{\Large{\frown}}{\mbox{AB}}\,=\,\stackrel{\Large{\frown}}{\mbox{AD}}\,=\,\stackrel{\Large{\frown}}{\mbox{DC}} }\)
半円を\(\,3\,\)等分しているので角度が具体的に出てきます。
中心角も円周角も三角定規のきれいな角度です。
なんだか安易すぎて何か勘違い?見落とし?しているのかな?
とも感じるけどこのまま進めます。笑
\(\,\mathrm{△ODC}\,\)が正三角形
ということに気がつけば面積はすべて出てきますが、方針は分かれるでしょうから少し説明を加えます。
\(\,\mathrm{BC}\,\)が直径であることと、
平行線から中点連結定理が言えることなどから長さなど分かることを書き込むと、
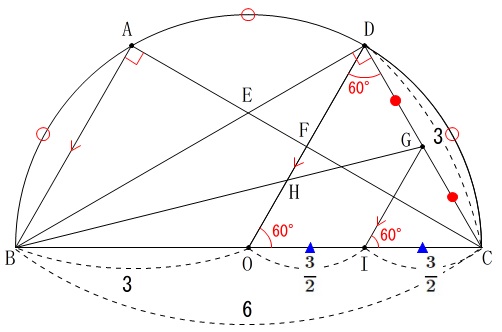 これから求める四角形\(\,\mathrm{OIGH}\,\)の面積は出せますが、
これから求める四角形\(\,\mathrm{OIGH}\,\)の面積は出せますが、
直角三角形があるので利用する方向で考えて見ましょう。
\(\,\mathrm{△BDC}\,\)に三平方の定理を用いて、
\(\begin{eqnarray}
\mathrm{BD^2+DC^2}&=&\mathrm{BC^2}\\
\mathrm{BD^2}+3^2&=&6^2\\
\mathrm{BD^2}&=&6^2-3^2\\
\mathrm{BD^2}&=&36-9\\
\mathrm{BD^2}&=&27\\
\mathrm{BD}&=&\pm 3\sqrt{3}
\end{eqnarray}\)
\(\,\mathrm{BD>0}\,\)(長さ)なので
\(\,\mathrm{BD=3\sqrt{3}}\,\)
三角定規の比 \(\,1:2:\sqrt{3}\,\) を使って
\(\begin{eqnarray}
\mathrm{DC:BD}&=&1:\sqrt{3}\\
3:\mathrm{BD}&=&1:\sqrt{3}\\
\mathrm{BD}&=&3\sqrt{3}
\end{eqnarray}\)
としても良いですが、角度に気がついていなくても出せるように三平方の定理を使っておきました。
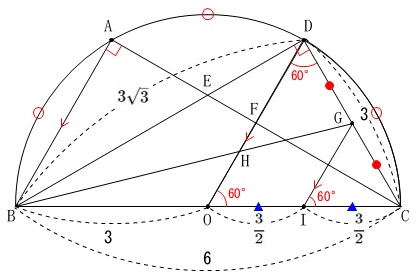 これで基準となる\(\,\mathrm{△BDC}\,\)の面積が出ます。
これで基準となる\(\,\mathrm{△BDC}\,\)の面積が出ます。
\(\begin{eqnarray}\displaystyle
\mathrm{△BDC}&=&\frac{1}{2}\times \mathrm{BD}\times \mathrm{DC}\\
&=&\frac{1}{2}\times 3\sqrt{3}\times 3\\
&=&\frac{9\sqrt{3}}{2}
\end{eqnarray}\)
ここからは線分比と相似比を利用した普通の面積縮小の繰り返しです。
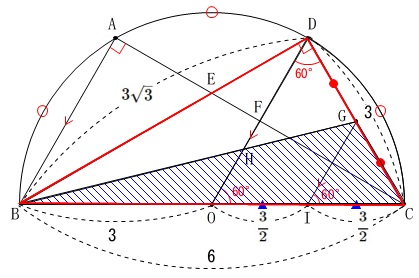
\(\,\mathrm{DG=GC}\,\)
より
\(\begin{eqnarray}\displaystyle
\mathrm{△BGC}&=&\frac{1}{2}\times \mathrm{△BDC}\\
&=&\frac{1}{2}\times \frac{9\sqrt{3}}{2}\\
&=&\frac{9\sqrt{3}}{4}
\end{eqnarray}\)
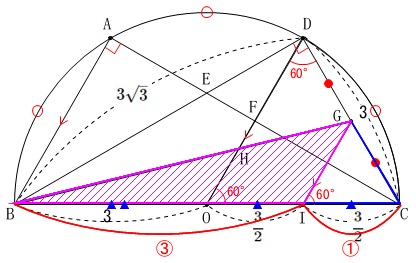 中点連結定理と半径やら直径から
中点連結定理と半径やら直径から
\(\mathrm{BI:IC}=3:1\)
だから
\(\begin{eqnarray}\displaystyle
\mathrm{△BGI}&=&\frac{3}{4}\times \mathrm{△BGC}\\
&=&\frac{3}{4}\times \frac{9\sqrt{3}}{4}\\
&=&\frac{27\sqrt{3}}{16}
\end{eqnarray}\)
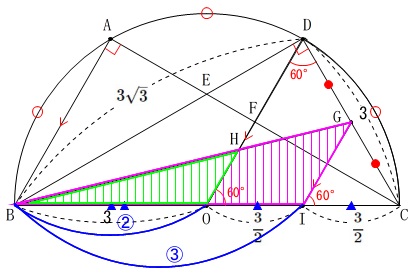 \(\,\mathrm{HO}\,\)∥\(\,\mathrm{GI}\,\)なので
\(\,\mathrm{HO}\,\)∥\(\,\mathrm{GI}\,\)なので
\(\,\mathrm{△BHO}\,\) ∽ \(\,\mathrm{△BGI}\,\)
で相似比は
\(\,\mathrm{BO:BI=2:3}\,\)
面積比は
\(\begin{eqnarray}
\mathrm{△BHO:△BGI}&=&2^2:3^2\\
&=&4:9
\end{eqnarray}\)
ここで
\(\,四角形\mathrm{OIGH}=\mathrm{△BGI-△BHO}\,\)
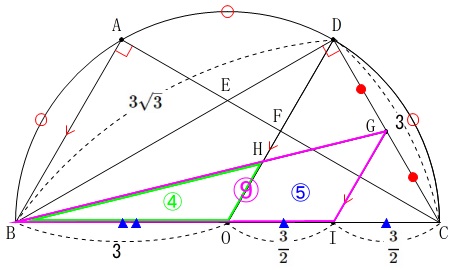
なので
\(\hspace{10pt}四角形\mathrm{OIGH}:\mathrm{△BGI}\\
=(9-4):9\\
=5:9\)
よって
\(\begin{eqnarray}\displaystyle
四角形\mathrm{OIGH}&=&\frac{5}{9}\times \mathrm{△BGI}\\
&=&\frac{5}{9}\times \frac{27\sqrt{3}}{16}\\
&=&\underline{ \frac{15\sqrt{3}}{16} }
\end{eqnarray}\)
ところで、会員に向けて書いておきますが、『約分の効用』は頭にありますよね?
ここでは途中の面積を具体的に求めていっていますが必要ありませんよ。

\(\begin{eqnarray}\displaystyle
四角形\mathrm{OIGH}&=&\mathrm{△BDC}\times \frac{1}{2}\times \frac{3}{4}\times \frac{5}{9}\\
&=&\frac{9\sqrt{3}\times 1\times 3\times 5}{2\times 2\times 4\times 9}\\
&=&\underline{ \frac{15\sqrt{3}}{16} }
\end{eqnarray}\)
途中計算は時間のムダです。
もう一つ、
 この時点で
この時点で
\(\,\mathrm{△ODC=△BGC}\,\)
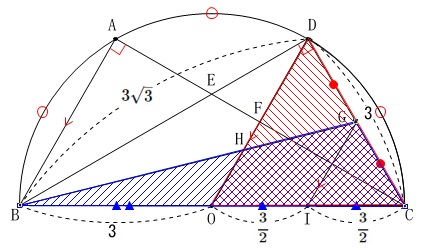
であることに気がついた人は違った計算をしているでしょう。
\(\,\mathrm{△ODC}\,\)は正三角形なので
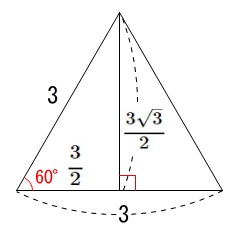
\(\begin{eqnarray}
\mathrm{△BGC}&=&\mathrm{△ODC}\\
&=&\frac{1}{2}\times 3\times \frac{3\sqrt{3}}{2}\\
&=&\frac{9\sqrt{3}}{4}
\end{eqnarray}\)
から縮小しても同じですので気にせず先に進んで良いですよ。
⇒ 2018年福岡県公立高校入試 数学問6の正四面体問題の解説
\(\large{\color{black}{\fbox{ 6 }}}\) は正四面体をあつかうので空間図形の問題です。
立体なのですが、、、え?という感じがしたでしょう。
基本レポート通りで十分に満点狙えますよ。
⇒ 福岡県公立高校入試問題2018(平成30年度)の数学の過去問解説
問\(\,1\,\)から見直しして\(\,60\,\)点狙いましょう。
