有機化合物の実験式や分子式を求める問題は、有機分野の計算問題として良く出されます。
実験式とは組成式のことですが、分子式との違いから説明しておきます。
問題となる化学反応自体は酸化(燃焼)か加水分解なので仕組みさえ知ってしまえば分子式の決定は難しくありません。
実験式と組成式と分子式
実験式と呼ばれる組成式は分子を構成している元素のモル比を最も簡単な比で表した式のことです。
組成式は分子を持たない物質を表す構成単位、として覚えているのですが、
意味的には「実験式」=「組成式」です。
分子式は分子を構成している原子の数そのものを表した化学式です。
例えば、
エタンの分子式は \(\mathrm{C_2H_6}\) です。
エタンの実験式(組成式)は、\(\mathrm{CH_3}\) です。
分子式が \(\mathrm{C_4H_8O_2}\) の化合物の、
実験式は \(\mathrm{C_2H_4O}\) です。
分かりますね。
では有機化学で使われる示性式と構造式についてももう一度確認しおきましょう。
示性式と構造式
例えばエタノール(エチルアルコール)の、
分子式は \(\mathrm{C_2H_6O}\) です。
各原子の公約数は1だけなので実験式も同じです。
しかし、この分子はアルコールという性質を持っているので、
\(\mathrm{C_2H_5\color{red}{OH}}\) のように官能基を組み合わせた形で表すことがあります。
これが「示性式」です。
有機化合物をあつかう場合は示性式を良く使います。
酢酸の示性式は \(\mathrm{CH_3\color{red}{COOH}}\) ですがよく見かけるのではないでしょうか。
「化学」では酢酸は \(\mathrm{C_2H_4O_2}\) とはあまり見ませんよね。
さらに、有機化合物の基本骨格は炭素です。
原子価4の炭素は結合状態によって直線構造も平面構造も立体構造もとります。
そこで分子式、示性式では情報が足りないという場合、
結合状態や立体的な構造も表現したい場合は「構造式」を使います。
炭素や水素や酸素とのつながりは価標と呼ばれる線で表し、
単結合のときは線1本 \(\mathrm{C-C}\)
二重結合のときは線2本 \(\mathrm{C=C}\)
三重結合のときは線3本 \(\mathrm{C\equiv C}\)
のように結合状態を示します。
もちろん有機化合物以外にも使いますが、高校生が見るのはほとんど有機化学分野だと思っていて良いでしょう。
本当は立体的な構造を示すため、角度や上下の向き具合も表現する方法はあるのですが、高校生は平面で表現出来れば十分です。
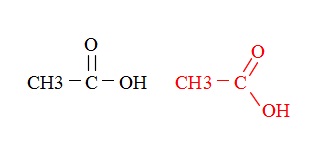
酢酸の構造式は左の酢酸で十分です。
実際にはカルボニル炭素は窮屈なので右の様に直線にはなっていません。
実験式を求める計算問題
\(\mathrm{C\,,\,H\,,\,O}\) からできた有機化合物がある。
その \(\,4.00\,\mathrm{mg}\,\) を燃焼させたら \(\,7.70\,\mathrm{mg}\,\) の \(\mathrm{CO_2}\) と \(\,4.59\,\mathrm{mg}\,\) の \(\mathrm{H_2O}\) ができた。
この化合物の実験式を求めよ。
\( \mathrm{C=12\,,\,H=1\,,\,O=16}\)
この化合物を燃焼させてできる物質は二酸化炭素と水だけです。
\( \mathrm{C}_a\mathrm{H}_b\mathrm{O}_c+x\,\mathrm{O_2}\\
\hspace{6pt}\rightarrow \hspace{4pt}a\,\mathrm{CO_2}+\displaystyle \frac{b}{2}\,\mathrm{H_2O}\)
もとの物質に酸素が加わり、二酸化炭素と水が出てきたということは、
できた二酸化炭素中の炭素と、水の中の水素は、
すべてもとの物質に含まれていたものだということが分かります。
そこで、
できた二酸化炭素と水から、もとの物質中の炭素と水素の質量を求めます。
二酸化炭素は \(\,7.70\,\mathrm{mg}\,\)できているので、その中に含まれる炭素は
\(\hspace{10pt}\displaystyle 7.70\times \frac{\mathrm{C}}{\mathrm{CO_2}}\\
\displaystyle =7.70\times \frac{12}{44}\\
=2.10 (\mathrm{mg})\)
水は \(\,4.59\,\mathrm{mg}\,\)できているので、その中に含まれる水素は
\(\hspace{10pt}\displaystyle 4.59\times \frac{\mathrm{2H}}{\mathrm{H_2O}}\\
\displaystyle =4.59\times \frac{2}{18}\\
=0.51 (\mathrm{mg})\)
もとの有機化合物は \(\,4.00\,\mathrm{mg}\,\) だったので、
その中の酸素の質量は、全体から炭素と水素の質量を引いて
\(\hspace{10pt}4.00-(2.10+0.51)\\
=1.39 (\mathrm{mg})\)
これで有機化合物を構成していた質量はそれぞれ分かりました。
実験式では「原子数の比」で表すので「モル比」に変える必要があります。
原子量で割ればモル比(原子数の比)が出ます。
\(\hspace{10pt}\mathrm{C\,:\,H\,:\,O}\\
=\displaystyle \frac{2.10}{12}\,:\,\displaystyle \frac{0.51}{1}\,:\,\displaystyle \frac{1.39}{16}\\ \\
=0.175\,:\,0.510\,:\,0.087\)
ここで実験式では各原子の比は整数となるので1番小さい数で割るときれいになることが多いです。
\(\hspace{10pt}\displaystyle \frac{0.175}{0.087}\,:\,\displaystyle \frac{0.510}{0.087}\,:\,\displaystyle \frac{0.087}{0.087}\\ \\
≒ \,\color{red}{2}\,:\,\color{red}{6}\,:\,\color{blue}{1}\)
これは比なので通分しても、\(\,1000\,\)倍してもかまいませんよ。
よって
実験式は \(\mathrm{C_\color{red}{2}H_\color{red}{6}O}\)
(酸素の「\(\,\color{blue}{1}\,\)」は省略します。)
これを分子式と見るとエタノールかジメチルエーテルだと推測はできますが、実験式なので断定はできません。
分子式を求めるには条件が不足しているのです。
実験式を求める問題では
「物質中の各原子の質量を求め、原子数の比を求める」
ことがポイントです。
例題を増やしても良いのですがどれも同じことの繰り返しになるので、
ちょっとだけひっかかりやすい問題を一問追加して先に進みましょう。
ある炭化水素を完全に燃焼したら、二酸化炭素 \(\,5.28\,\mathrm{mg}\,\)と水 \(\,2.16\,\mathrm{mg}\,\)が生成した。
この炭化水素の実験式を求めよ。
\( \mathrm{C=12\,,\,O=16\,,\,H=1}\)
「あれ?もとの物質の質量が書いてない。」
と気がついたあなたは鋭い!と同時に見落としています。
この問題で見逃してはいけないのは「炭化水素」という物質です。
炭化水素は酸素を含有していません。
例題1を思い出して欲しいのですが、
発生した二酸化炭素からもとの物質中の炭素の質量、
発生した水からもとの物質中の水素の質量をもとめ、
これらをもとの物質量から引くことで酸素の質量を計算しました。
しかし、
炭化水素では酸素の質量を求めなくて良いのです。
実は炭化水素の場合、二酸化炭素中の炭素、水の中の水素の質量も求めなくても組成比は出せるのですが、例題1の場合にも使えるように質量を求めてモル比に変える方法で示します。
発生した \(\mathrm{CO_2}\) と \(\mathrm{H_2O}\) から炭化水素を構成する炭素と水素の質量比は
\(\hspace{10pt} \mathrm{5.28\times \displaystyle \frac{C}{CO_2}\,:\,2.16\times \displaystyle \frac{2H}{H_2O}}\\
=\,5.28 \times\displaystyle \frac{12}{44}\,:\,2.16\times \displaystyle \frac{2}{18}\)
(ここは計算してもかまいません。)
原子量は \(\mathrm{C=12\,,\,H=1}\) なので原子数の比は
\(\hspace{10pt} \mathrm{C:H}\\
=5.28 \times\displaystyle \frac{12}{44}\times \displaystyle \frac{1}{12}:2.16\times \displaystyle \frac{2}{18}\times \displaystyle \frac{1}{1}\\
=1:2\)
実験式は \(\mathrm{CH_2}\) です。
もとの物質に酸素が含まれている場合が多いので例題1のタイプの問題を練習しておくと良いですね。
分子式を決定する問題
実験式を求める問題から分子式を求める問題に格上げです。w
実験式を求める問題と分子式を求める問題と何が違うかというと、
「条件が多くなっているだけ」
ですので心配することはありません。
いろいろな条件がプラスされることで分子式を求めることができるようになるのですが、
多くの場合、「分子量」です。
先に分子量を求めさせて分子式の決定が後という場合もありますが、
分子量が分かっていないと分子式は求めにくいです。
だから「分子式を求めよ」という問題は、分子量をチェックしておくことがポイントです。
実験式が求められているならそれぞれの原子を同じだけ倍して、分子量を一致させることで分子式が求まるはずですからね。
例えば
実験式 \(\mathrm{CH_3}\)
分子量 \(30\)
だとすると、\(\mathrm{CH_3}=15\) なので \(\mathrm{C_2H_6}\) と2倍すれば分子量が一致します。
よってこの物質の分子式は \(\mathrm{C_2H_6}\) だと分かるということです。
分子量に注目ですよ。
\(\mathrm{C\,,\,H\,,\,O}\) からできている化合物 \(\,2.175\,\mathrm{mg}\,\) を完全に燃焼させたところ、
\(\mathrm{CO_2}\) が \(\,3.159\,\mathrm{mg}\,\) と \(\mathrm{H_2O}\) が \(\,1.305\,\mathrm{mg}\,\) 得られた。
また、この化合物の分子量を測定した結果は \(\,180\,\) であった。
この化合物の組成式と分子式を求めよ。
\( \mathrm{C=12\,,\,H=1\,,\,O=16}\)
分子量が \(\,180\,\) ということから「ブドウ糖かな?」くらいは想像出来ますが、
そんな単純に考えてもいけません。
組成式(実験式)も求めることになっているし、
化合物中の炭素と水素と酸素の質量を求めましょう。
化合物中の \(\mathrm{C,H,O}\) の質量は、
\(\begin{eqnarray}
\mathrm{C}&:&\,3.159\times \mathrm{\displaystyle \frac{C}{CO_2}}\\
&=&3.159\times \displaystyle \frac{12}{44}\\
&≒& 0.8615
\end{eqnarray}\)
\(\begin{eqnarray}
\mathrm{H}&:&\,1.305\times \mathrm{\displaystyle \frac{2H}{H_2O}}\\
&=&1.305\times \displaystyle \frac{2}{18}\\
&=&0.145
\end{eqnarray}\)
\(\begin{eqnarray}
\mathrm{O}&:&\,2.176-(0.8615+0.145)\\
&≒& 1.170\end{eqnarray}\)
これらから \(\mathrm{C,H,O}\) の原子数の比は
\(\begin{eqnarray}
\mathrm{C:H:O}&=&\displaystyle \frac{0.8615}{12}:\displaystyle \frac{0.145}{1}:\displaystyle \frac{1.170}{16}\\ \\
&≒& 0.072:0.145:0.073\\ \\
&≒& 1:2:1
\end{eqnarray}\)
よって組成式(実験式)は \(\mathrm{CH_2O}\)
またこの組成式の式量の整数倍が分子量に等しくなるので、
\(\hspace{10pt}\mathrm{(CH_2O)\times n=180}\\ \\
\Leftrightarrow \hspace{10pt} (12+1\times2+16)\times n=180\\ \\
\Leftrightarrow \hspace{10pt} n=6\)
すべての原子数を\(\,6\,\)倍して
分子式 \(\mathrm{\underline{ C_6H_{12}O_6 }}\)
分子式を求める問題の形はいろいろありますがこれが1番基本的なものとなります。
もちろん他にも解き方はあります。
しかし、構成元素の質量比からモル比へ変換する、この方法を先ずは覚えておきましょう。
物質量である「モル(mol)」はどこまでもついてきますよ。