2018年青森県公立高校入試数学の過去問第2問の解説

青森県で2018年(平成30年度)に行われた公立高校入試の数学過去問第2問の解説です。
第2問は確率と連立方程式の問題が2つ並べてあります。
日本文も長くはなくて、ルールも読み取りやすいので短時間で終わらせることができます。

問題は青森県の公式サイトで公開してくれています。

⇒　青森県2018年公立高校入試数学問題

確率問題を解くときのポイント

(1)は確率の問題です。
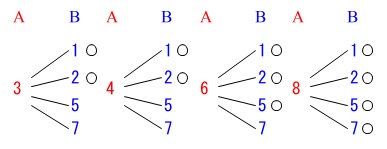
確率の問題でまず最初にやることは『樹形図』を書くことです。

その前にルールを読み取ることは当然ですが、手を動かして確認しないとルールは読み取れませんよ。
大きな問題ではルール確認の問題があったり、具体例が書かれていたりしますが、この問題はそこまでする必要がない程基本的な問題になっています。

ルールの確認をしておきます。

　\(\,\mathrm{A}\,\)という袋に\(\,3,4,6,8\,\)の\(\,4\,\)枚のカード
　\(\,\mathrm{B}\,\)という袋に\(\,1,2,5,7\,\)の\(\,4\,\)枚のカード

があって、一枚ずつ取り出す。

　\(\,\mathrm{A＞B}\,\)となる確率を求める。

例えば、

\(\,\mathrm{A}\,\)から\(\,3\,\)を取り出したとき\(\,\mathrm{B}\,\)から\(\,1\,\)を取り出したときは
\(\,\color{red}{3＞1}\,\)なので\(\,\mathrm{A＞B}\,\)という条件を満たします。

\(\,\mathrm{A}\,\)から\(\,3\,\)を取り出したとき\(\,\mathrm{B}\,\)から\(\,7\,\)を取り出したときは
\(\,\color{red}{3＜7}\,\)なので\(\,\mathrm{A＞B}\,\)という条件を満たしません。　

樹形図でも良いですがあきてきていると思うので表にしてみます。笑

　縦が\(\,\mathrm{A}\,\)から取り出した数字
　横が\(\,\mathrm{B}\,\)から取り出した数字
表中の\(\,\color{magenta}{○}\,\)は\(\,\mathrm{A＞B}\,\)となっている場合です。
を表しています。
　\(\begin{array}{|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{5} & \color{blue}{7} \\ \hline
\color{red}{3} & \color{magenta}{○} & \color{magenta}{○} & & \\ \hline
\color{red}{4} & \color{magenta}{○} & \color{magenta}{○} & & \\ \hline
\color{red}{6} & \color{magenta}{○} & \color{magenta}{○} & \color{magenta}{○} & \\ \hline
\color{red}{8} & \color{magenta}{○} & \color{magenta}{○} & \color{magenta}{○} & \color{magenta}{○} \\ \hline
\end{array}\)
　
全部で\(\,16\,\)通りの取り出し方がある中で\(\,\mathrm{A＞B}\,\)を満たすのは\(\,11\,\)通りなので、
　（答え）　\(\displaystyle\underline{　\frac{11}{16}　}\)

(2)は［ルール］とあるので確率の続きかと思いましたが違ってました。
問題はよく読みましょう。

［ルール］\(\,\mathrm{N}\,\)と\(\,\mathrm{A}\,\)の二人でじゃんけんをする。

\(\,①\,\)じゃんけんは\(\,15\,\)回。あいこも\(\,1\,\)回と数える。

\(\,②\,\)勝った場合は\(\,2\,\)点、負けた場合は\(\,-1\,\)点、あいこの場合は\(\,1\,\)点。

例えば、
　\(\,\mathrm{N}\,\)さんが\(\,15\,\)回全部勝てば、\(\,\mathrm{N}\,\)さんは\(\,30\,\)点、\(\,\mathrm{A}\,\)さんは\(\,-15\,\)点
　\(\,15\,\)回全部あいこだった場合、\(\,\mathrm{N}\,\)さんも\(\,\mathrm{A}\,\)さんも\(\,15\,\)点
になります。

問題を解いてみましょう。

ア
　\(\,\mathrm{N}\,\)さん\(\,12\,\)点
　\(\,\mathrm{A}\,\)さん\(\,6\,\)点
のとき
　\(\,\mathrm{N}\,\)さんが勝った回数を\(\,x\,\)回
　\(\,\mathrm{A}\,\)さんが勝った回数を\(\,y\,\)回
として連立方程式を立てます。

あいこの回数は必要無いのか？
という疑問を持った人は良いですね～。

あいこの回数も\(\,x,y\,\)を使って表します。

\(\,\mathrm{A}\,\)さんが\(\,y\,\)回勝ったら、\(\,\mathrm{N}\,\)さんは\(\,y\,\)回負けています。
「勝つ」か「負ける」か「あいこ」しかないので、
\(\,\mathrm{N}\,\)さんについて見ても\(\,\mathrm{A}\,\)さんについて見ても
　勝ち＋負け＋あいこ\(\,=15\,\)
なので
　あいこ\(\,=15-\,\)勝ち－負け

\(\,15\,\)回のうち、\(\,\mathrm{N}\,\)さんが\(\,\color{red}{x}\,\)回、\(\,\mathrm{A}\,\)さんが\(\,\color{blue}{y}\,\)回勝ったとすると、
あいこの回数は
　\(\color{green}{15-x-y}\)　回
となります。

\(\,\mathrm{N}\,\)さんの得点は\(\,\color{red}{12}\,\)点です。

　勝ち\(\,x\,\)　負け\(\,y\,\)　あいこ\(\,15-(x+y)\,\)
なので
　\(\,2\times x+(-1)\times y+1\times (15-x-y)=\color{red}{12}\,\)

\(\,\mathrm{A}\,\)さんの得点は\(\,\color{blue}{6}\,\)点です。

　勝ち\(\,y\,\)　負け\(\,x\,\)　あいこ\(\,15-(x+y)\,\)
なので
　\(\,2\times y+(-1)\times x+1\times (15-x-y)=\color{blue}{6}\,\)　

(1)は立式だけです。
　\( \begin{cases}
\hspace{7pt} 2x-y+(15-x-y)=12\\ \\
\hspace{7pt} 2y-x+(15-x-y)=6
\end{cases}\)

これはそれぞれの項に意味のある方程式で立式の答えとして良いと思うのですが青森県は認めないようです。

（答え）
　\( \begin{cases}
\hspace{7pt} x-2y=-3\\ \\
\hspace{7pt} -2x+y=-9
\end{cases}\)

これは上の式を整理したものなのでまだ分かります。

しかし、解答の備考欄に

『
　\( \begin{cases}
\hspace{7pt} x+y=12\\ \\
\hspace{7pt} 2x-y=9
\end{cases}\)
や
　\( \begin{cases}
\hspace{7pt} x+y=12\\ \\
\hspace{7pt} x-2y=-3
\end{cases}\)
も正解とする。』

となっています。
明らかに上の第1方程式は回数の方程式ですよね。
どこからおあいこの回数が\(\,3\,\)回と分かったのでしょう？

個人的には
　\( \begin{cases}
\hspace{7pt} 2x-y+(15-x-y)=12\\ \\
\hspace{7pt} 2y-x+(15-x-y)=6
\end{cases}\)
と書いた中学生には二重丸をあげます。笑
しかし、私は青森県の採点者ではありませんので青森県の学校の先生に聞いて下さい。
日本全国同じ教科書なのにおかしな話ですが、都道府県で採点基準（立式の正答）が違いますから。
※
（かっこ）はない形で書きなさいという指示がある場合がありますのでそのときは（かっこ）を外して整理して下さい。
指示がなくても（かっこ）は外して整理した方が無難です。

イは連立方程式を解くだけです。
　　\( \begin{cases}
\hspace{7pt} 2x-y+(15-x-y)=12\\ \\
\hspace{7pt} 2y-x+(15-x-x)=6
\end{cases}\)
は同類項をまとめると
　\( \begin{cases}
\hspace{7pt} x-2y=-3\\ \\
\hspace{7pt} -2x+y=-9
\end{cases}\)

連立方程式を解く基本は一文字消去です。
\(\,x,y\,\)のどちらを消去してもかまいません。

\(\,x\,\)を消去して\(\,y\,\)を先に求めましょう。

上の式を両辺2倍して
　\(\,2x-4y=-6\,\)
これと連立方程式の下の式を両辺をそれぞれ加えましょう。

　\(\hspace{23pt}2x-4y=-6\\
\underline{+)-2x+\hspace{4pt}y=-9　}\\
\hspace{34pt}-3y=-15\\
\hspace{50pt}y=5\)

これをどれでも良いので方程式に戻します。

　\(\begin{eqnarray}
x-2y&=&-3\\
x-2(5)&=&-3\\
x-10&=&-3\\
x&=&7
\end{eqnarray}\)

（答え）
　なつさん　\(\,\underline{　7　}\,\)回
　あきさん　\(\,\underline{　5　}\,\)回

\(\large{\color{black}{\fbox{　2　}}}\)　はここまでです。

⇒　2018年青森県公立高校入試数学の過去問第3問の解説

\(\large{\color{black}{\fbox{　3　}}}\)　は平面図形と空間図形（正四面体）の問題です。
基本的なものですのでしっかりと作業すればさらりと答えまでたどり着けます。

⇒　青森県公立高校入試2018数学の過去問と解説

\(\large{\color{black}{\fbox{　1　}}}\)　とここの\(\large{\color{black}{\fbox{　2　}}}\)までで\(\,52\,\)点配点されています。