2018年（平成30年）度に福岡県で行われた公立高校入試の数学（問6の空間図形）問題の解説です。
立体は正四面体をあつかいますが、立体問題は相似比だけで答えが出ます。
これが空間図形の問題に見える人は少し問題への取り組みを変えた方が良いかもしれません。
問題は福岡県の公式サイトにもあります。
相似比と体積比
\(\large{\color{black}{\fbox{ 6 }}}\)は拍子抜けするくらいの問題なので簡単に説明します。
問題に正四面体の図があるので利用しましょう。
わざわざいう必要はないことですが、正四面体はすべての面が正三角形です。
(1)問題の条件を書き出しておきます。
\(\,\mathrm{OD:DA=1:2}\,\)
\(\,\mathrm{OE:EB=1:2}\,\)
\(\,\mathrm{OF:FC=1:2}\,\)
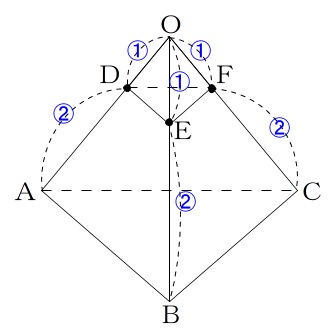
\(\,1\,\)辺の長さが\(\,8\,\)という条件はありますが(1)では使いません。
\(\,3\,\)点\(\,\mathrm{D,E,F}\,\)を通る平面でこの正四面体を切ったとき、
下にできる台の形をした立体を「すい台」といいます。
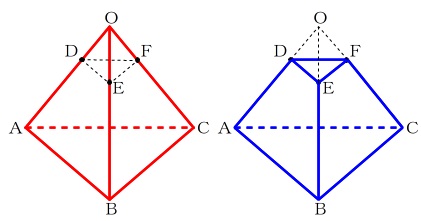
問題は「すい台の体積はもとの正四面体の何倍か」です。
すい台の方が小さいので\(\,1\,\)倍よりは小さいことは分かります。
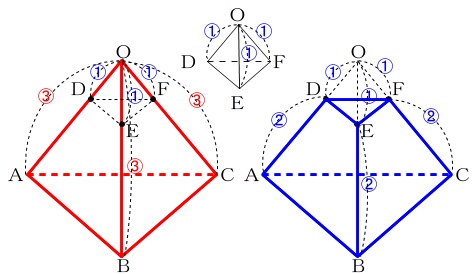正四面体\(\,\mathrm{O-ABC}\,\)と\(\,\mathrm{O-DEF}\,\)は相似です。
相似比は \(\,3：1\,\)
なので
体積比は \(\,3^3:1^3=27:1\,\)
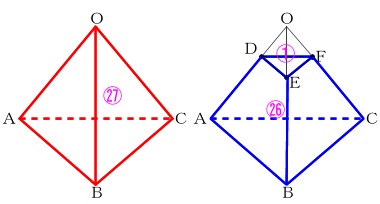
すい台は\(\,\mathrm{O-ABC}\,\)から\(\,\mathrm{O-DEF}\,\)を引いたものなので
\(\hspace{10pt}(正四面体の体積)：(すい台の体積)\\
=27:(27-1)\\
=27:26\)
よってすい台は正四面体の体積の
\(\displaystyle \underline{ \frac{26}{27} 倍 }\)
これは体積比なので空間、立体ぽいですね。
意外なのは次です。
空間図形の取り組み方
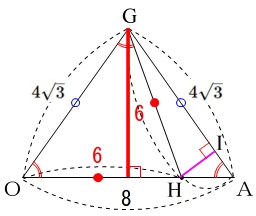
(2)\(\,1\,\)辺\(\,8\,\)の正四面体は同じです。
条件は
\(\,\mathrm{G}\,\)は\(\,\mathrm{BC}\,\)の中点
\(\,\mathrm{H}\,\)は\(\,\mathrm{OA}\,\)上で\(\,\mathrm{OH=GH}\,\)
\(\,\mathrm{H}\,\)から\(\,\mathrm{AG}\,\)に垂線を引き交点を\(\,\mathrm{I}\,\)
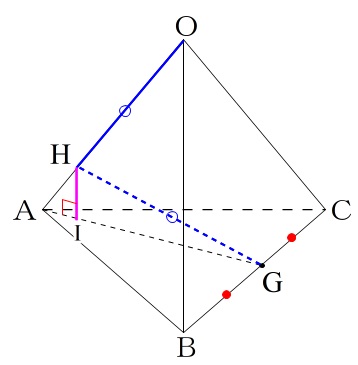
このときの\(\,\mathrm{HI}\,\)の長さを求めます。
立体の中にある線分の長さを求めたいときはその線分を含む面を抜き出します。
多くの立体問題ではいくつかの面を抜き出すことになるのですが、正四面体の場合は長さがある程度分かるので少なくて済みます。
実際この問題は\(\,1\,\)つの面を抜き出してすぐに答えが出たのですが、ここでは他の問題にも通用するようにていねいにやっておきます。
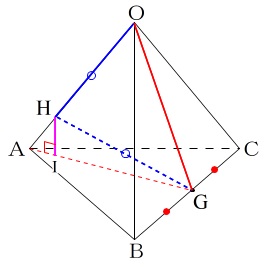線分\(\,\mathrm{HI}\,\)の長さを求めたいので\(\,\mathrm{HI}\,\)を含む平面を抜き出します。
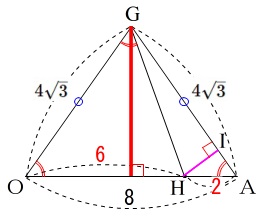
この場合選ぶ必要もなく\(\,\mathrm{△OAG}\,\)です。
非常に分かり易いですね。
ただし、長さには一切触れてきてませんので長さを出しておきましょう。
正四面体の1辺なので
\(\,\mathrm{OA=8}\,\)
これはすぐに分かります。
\(\,\mathrm{OG}\,\)と\(\,\mathrm{AG}\,\)は正三角形の高さになる長さです。
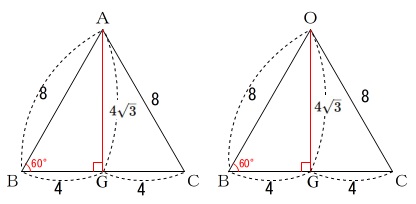三角定規の比になるので
\(\,\mathrm{OG=AG}\,=4\sqrt{3}\)
弧の長さをある程度イメージしながら\(\,\mathrm{△OAG}\,\)を抜き出しましょう。
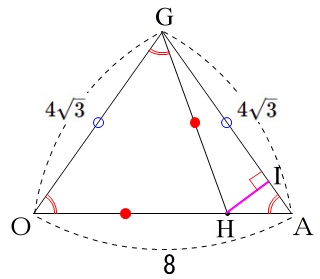\(\,\mathrm{HI}\,\)の長さを求めたいけど直接はでません。
長さを求めるときは、合同か、相似か、三平方の定理がほとんどです。
1つの図形の面積が変わらないことから、図形を転がして面積と高さの関係を利用するという方法はありますが、
それは相似や三平方の定理を利用して面積を出しているはずです。
三平方の定理も面積も使えそうですが、相等遠回りになりそうなので、相似を探しましょう。
相似な二等辺三角形があります。
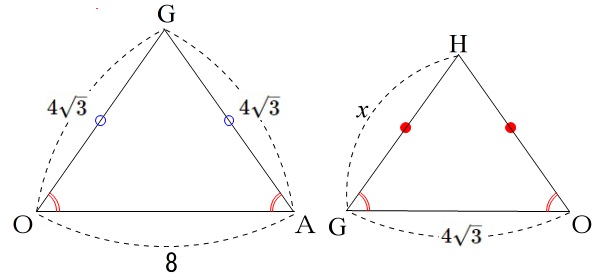
\(\,\mathrm{△GOA}\,\) ∽ \(\,\mathrm{△HGO}\,\)
相似は（合同も含めて）無条件に探すようにしておきましょう。
ニコちゃんマークです。
\(\begin{eqnarray}
\mathrm{GO:HG}&=&\mathrm{OA:GO}\\
4\sqrt{3}:x&=&8:4\sqrt{3}\\
8x&=&4\sqrt{3}\times 4\sqrt{3}\\
&=&48\\
x&=&6
\end{eqnarray}\)
この長さを求めたのは、手がかりとなる長さ\(\,\mathrm{AH}\,\)や\(\,\mathrm{OH}\,\)が欲しかったからですが、
相似を見つけたら出せる長さは出しておくと良いです。
\(\,\mathrm{OH=HG}\,\)という条件はそのために与えてくれているのです。
これがなければ\(\,\mathrm{HI}\,\)は求めることはできません。
\(\,\mathrm{OH=HG=6}\,\)と分かったので
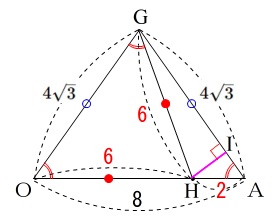\(\,\mathrm{OA=8}\,\)から
\(\,\mathrm{AH=OA-OH=2}\,\)
これで垂線\(\,\mathrm{HI}\,\)の長さが求めることができます。
パッと思い浮かぶ方向性が3つあるので示しておきます。
（他にもあるかもしれないけど考えていません。笑）
①\(\,\mathrm{△HOG}\,\)で\(\,\mathrm{H}\,\)から\(\,\mathrm{OG}\,\)に垂線を引き相似を利用して求める方法。
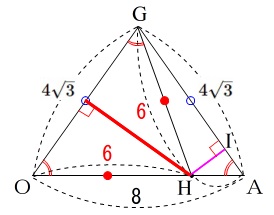
②\(\,\mathrm{△AHG}\,\)に三平方の定理を直接用いて求める方法。
③\(\,\mathrm{△GOA}\,\)の高さを求めて面積を利用する方法。
順に説明します。
①\(\,\mathrm{H}\,\)から\(\,\mathrm{OG}\,\)に垂線を引いて交点を\(\,\mathrm{K}\,\)とします。
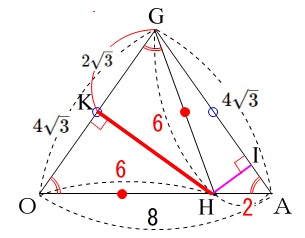\(\,\mathrm{△HGK}\,\) ∽ \(\,\mathrm{△HAI}\,\)
なので
\(\,\mathrm{HG:HA=\color{red}{HK}:\color{magenta}{HI}}\,\)
（ここで会員は何するか分かりますよね？）
\(\,\mathrm{\color{magenta}{HI}}\,\)に対する辺\(\,\mathrm{\color{red}{HK}}\,\)を三平方の定理で求めます。
\(\begin{eqnarray}
\mathrm{\color{red}{HK}^2+GK^2}&=&\mathrm{HG^2}\\
\mathrm{\color{red}{HK}^2}&=&\mathrm{HG^2-GK^2}\\
&=&6^2-(2\sqrt{3})^2\\
&=&36-12\\
&=&24\\
\mathrm{\color{red}{HK}}&=&\pm 2\sqrt{6}
\end{eqnarray}\)
\(\,\mathrm{\mathrm{\color{red}{HK}}＞0}\,\)なので
\(\mathrm{\color{red}{HK}}=\color{red}{2\sqrt{6}}\)
よって
\(\begin{eqnarray}\displaystyle
\mathrm{HG:HA}&=&\mathrm{\color{red}{HK}:\color{magenta}{HI}}\\
6:2&=&\color{red}{2\sqrt{6}}:\mathrm{\color{magenta}{HI}}\\
6\times \mathrm{\color{magenta}{HI}}&=&2\times 2\sqrt{6}\\
\mathrm{\color{magenta}{HI}}&=&\frac{4\sqrt{6}}{6}\\
&=&\underline{ \frac{2\sqrt{6}}{3} }
\end{eqnarray}\)
相似利用することを考えるとこれが普通かな？
②\(\,\mathrm{△AHG}\,\)に三平方の定理を直接用いて求める方法。
ここまでくれば教科書でもやったことがある問題でしょう。
\(\,\mathrm{△AHI}\,\)と\(\,\mathrm{△GHI}\,\)に三平方の定理を使います。
\(\,\mathrm{AI}=\color{red}{x}\,\)とすると\(\,\mathrm{GI}=(\,\color{red}{4\sqrt{3}-x}\,)\,\)なので
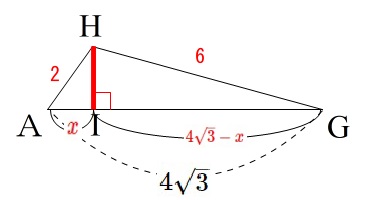
\(\,\mathrm{△AHI}\,\)に三平方の定理を用いると
\(\begin{eqnarray}
\mathrm{\color{red}{HI^2}+AI^2}&=&\mathrm{AH^2}\\
\mathrm{\color{red}{HI^2}}&=&\mathrm{AH^2-AI^2}\\
&=&\color{red}{2^2-x^2} ･･･④
\end{eqnarray}\)
また\(\,\mathrm{△GHI}\,\)に三平方の定理を用いると
\(\begin{eqnarray}
\mathrm{\color{red}{HI^2}+GI^2}&=&\mathrm{GH^2}\\
\mathrm{\color{red}{HI^2}}&=&\mathrm{GH^2-GI^2}\\
&=&6^2-(x-4\sqrt{3})^2\\
&=&36-(x^2-8\sqrt{3}x+48)\\
&=&36-x^2+8\sqrt{3}x-48\\
&=&\color{red}{-x^2+8\sqrt{3}x-12} ･･･⑤
\end{eqnarray}\)
この2つの\(\,\mathrm{HI^2}\,\)は等しいので
\(\begin{eqnarray}\displaystyle
\color{red}{2^2-x^2}&=&\color{red}{-x^2+8\sqrt{3}x-12}\\
4&=&8\sqrt{3}x-12\\
16&=&8\sqrt{3}x\\
x&=&\frac{16}{8\sqrt{3}}\\
&=&\frac{2}{\sqrt{3}}\\
&=&\frac{2\sqrt{3}}{3}
\end{eqnarray}\)
これは求める\(\,\mathrm{\color{red}{HI}}\,\)ではありません。
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{HI^2}}&=&\mathrm{AH^2-AI^2}\\
&=&2^2-x^2\\
&=&2^2-\left(\frac{2\sqrt{3}}{3}\right)^2\\
&=&4-\frac{12}{9}\\
&=&\frac{4\times 9-12}{9}\\
&=&\color{red}{\frac{24}{9}}\\
\mathrm{\color{red}{HI}}&=&\underline{ \frac{2\sqrt{6}}{3} } (\mathrm{HI}＞0)
\end{eqnarray}\)
『覚え太郎』会員は\(\,④=⑤\,\)を直接おいて求めても良いですよ。
ここでは理由は書かなくて良いので途中のめんどくさい関係式は不要です。
私は次が待っていると思っていて③の方法で解いたのですが、
ここで問題が終わっていたので③は省略します。
（決してめんどくさくなってきたわけではありません。笑）
③\(\,\mathrm{△GOA}\,\)の高さを求めて面積を利用する方法というのは
\(\,\mathrm{△AGH}\,\)の面積は\(\,\mathrm{△GOA}\,\)の面積の\(\displaystyle \frac{1}{4}\)です。
\(\,\mathrm{△AGH}\,\)の面積は
\(\displaystyle \frac{1}{2}\times \mathrm{AG}\times \mathrm{HI}\)
なので面積を利用して\(\,\mathrm{HI}\,\)を求めただけです。
1つの三角形を転がしても面積は変わらない
というのを利用する問題が多いのでそちらに行ってしまいました。
相似を利用する①がはやいでしょう。
試験場ではあれこれ悩むより、作業を終えて思いついた方法があればそれで突き進んだ方がはやいですよ。
解答2つ書いて点数に倍くれるなら良いですが、そんなことありませんからね。
しかもこの問題は答えだけなので、正解として1つしか書きようがありません。笑
ただ、数学の解法が1つでは無いということは覚えておいて下さい。
今更いうまでもありませんが、立体は立体のまま考えない、というのは空間図形問題攻略のポイントです。
立体中から、平面を抜き出して考えるということです。
空間図形はおおよその形を書くのも苦労するでしょう？
図を書かない人はイメージでやってるんでしょうかね。
書かなくてもイメージできる程すごいのか、解く気がないかのどちらかですね。
平面はなんとかなる、という人は空間図形の問題では必要な平面を抜き出してみて下さい。
当たり前のことですが、空間が平面でできているということを実感できます。笑
普通ならいくつか平面を抜き出して組み合わせるのですが、
この問題は正四面体なので問題慣れしていれば1つの平面で終わります。
それでも今回の解説のように抜き出しはいつもするようにした方が良いですね。
⇒ 福岡県公立高校入試問題2018(平成30年度)の数学の過去問解説
全体でどのくらいの分量かもう一度確認しておくと良いです。
毎年、問題は変わっても問題や計算の量はそれほど変わるものではありません。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
