青森県公立高校入試2018数学の過去問と解説

青森県で2018年(平成30年度)に行われた公立高校入試の数学の過去問と解説です。
問1はの式の計算、方程式、資料の活用、図形の基本問題など小問集合になります。
中学で習った数学の基本用語をしっかり理解していれば難しい問題はありませんが、1つだけ確認しておいて欲しいことがあります。

問題は青森県の公式サイトで公開してくれています。

⇒　青森県2018年公立入試数学問題

\(\large{\color{black}{\fbox{　1　}}}\)　中学3年間の数学の基本確認の小問集合になっています。

\(\color{black}{\fbox{　1　}}\)の解説の最後に知っておいて欲しいことを書いておきます。

正の数負の数と文字式の計算問題

(1)には5問の計算問題があります。

簡単なのでミスしにくい計算方法を身につけておくと良いですよ。

ア
　\(\hspace{10pt}-6-3\\
=\underline{-9}\)

マイナスするということは数直線で左に移動するということです。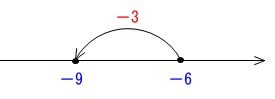

イ
　\(\hspace{10pt}7+2\times (-3^2)\\
=7+2\times (-9)\\
=7-18\\
=\underline{-11}\)

計算順序は、足し算引き算よりかけ算割り算が先です。
かけ算割り算よりも（かっこ）の中が先です。

　\((-3)^2=(-3)\times (-3)=+9\)
　\((-3^2)=-(3\times 3)=-9\)

の違いは良いですね？

ウ
　\(\hspace{10pt}\displaystyle 9\,a^2\,b\color{red}{\div \frac{3}{2}\,a\,b} \times b\\
\displaystyle =9\,a^2\,b\color{red}{\times \frac{2}{3\,a\,b}}\times b\\
=6\,a\,b\)

割り算は逆数のかけ算です。

　\(\displaystyle \frac{3}{2}\,a\,b\) の\(\,a\,b\,\)は分子に乗っている
ことを忘れないようにして下さい。
　\(\displaystyle \frac{3}{2}\,a\,b=\frac{3\,a\,b}{2}\)

だから逆数をかけるときは
　\(\displaystyle \times \frac{2}{3\,a\,b}\)
となります。

『覚え太郎』会員は分数計算は足し算や引き算が混じって途中で途切れようが
　\(\displaystyle \frac{9\,a^2\,b\times 2\times b}{3\,a\,b}\)
と分数線を1つしか書かないやり方で高校卒業まで通して良いです。

エ
　\(\hspace{10pt}\displaystyle \frac{6x+y}{4}-\frac{x-7y}{2}\\
\displaystyle =\frac{(6x+y)-2(x-7y)}{4}\\
\displaystyle =\frac{6x+y-2x+14y}{4}\\
\displaystyle =\frac{4x+15y}{4}\)

分数線は1つで十分です。

分子には（かっこ）がついていることを忘れないようにしましょう。

それと、
　\(\displaystyle \frac{4x+15y}{4}\\
\displaystyle =\frac{4x}{4}+\frac{15y}{4}\\
\displaystyle =x+\frac{15y}{4}\)

とするのはかまいませんが、
　\(\displaystyle \frac{4x+15y}{4}\)
の\(\,x\,\)の係数と分母が約分できるからといって部分的に約分することはできませんよ。

例えば
　\(\hspace{10pt}\displaystyle \frac{\color{red}{12}x+15y}{\color{red}{8}}\\
\displaystyle =\frac{\color{red}{3}x+15y}{\color{red}{2}}\)
なんてことはできません。

　\(\hspace{10pt}\displaystyle \frac{12x+15y}{8}\\
\displaystyle =\frac{3x}{2}+\frac{15y}{8}\)

と分母を分けて書くなら問題ありません。
しかし、
　\(\displaystyle \frac{12x+15y}{8}\)
のままでも良いでしょう？

ただし、
　\(\hspace{10pt}\displaystyle \frac{\color{red}{12}x+\color{red}{16}y}{\color{red}{8}}\\
\displaystyle =\frac{3x+4y}{2}\)
のようにすべての項が同時に約分できるときは約分しなければなりません。

オ
　\(\hspace{10pt}(x-1)^2-(x+2)(x-6)\\
=(x^2-2x+1)-(x^2-4x-12)\\
=x^2-2x+1-x^2+4x+12\\
=2x+13\)

展開公式を覚えていない、という人も少ないとは思いますが、
展開は公式を使わなくても答えは出ます。

　\(\hspace{10pt}(x-1)^2-(x+2)(x-6)\\
=(x-1)(x-1)-(x+2)(x-6)\\
=(x^2-x-x+1)-(x^2-6x+2x-12)\\
=(x^2-2x+1)-(x^2-4x-12)\\
=x^2-2x+1-x^2+4x+12\\
=2x+13\)

しかし、
この程度の公式を使いこなそうとせず、算数を続け、
数学をしようとしないのであれば高校では数学でかなり苦労することを覚悟しておきましょう。

この展開は暗算しようと思えばできる範囲ではありますが、
2行目、3行目を書くことで確実に計算ミスは減ります。

問題用紙も次の問題への間を開けてくれています。
青森県の問題はものすごく親切な配置をしてくれていますので、しっかり利用させてもらいましょう。

他県ではどこで計算しろっての？というくらい意地悪な問題が並ぶところもあります。
（どことはいいませんよ。笑）
それと比べたらこの問題は受験生思いの問題です。

割り算の基本原則と代入計算問題

(2)
　「\(\,a\,\)本の鉛筆を、\(\,5\,\)本ずつ\(\,b\,\)人に配ると\(\,3\,\)本余る。」

これは言い換えると

　\(\,a\,\)を\(\,5\,\)で割ると商が\(\,b\,\)であまりが\(\,3\,\)

と同じです。

これを算数のように
　\(\displaystyle \frac{a}{5}=b\,\ldots \,3\)
とすることは数学ではありません。

会員にこれを説明するのは「めんどくさい」以外の何物でもないのですが、
（いいたいことわかるでしょ？笑）

割り算の原則は日本の小学校でやっているような算数のものではありません。

　\(\,\color{red}{(もとの数)=(割る数)\times (商)+(余り)}\,\)

これが割り算の基本原則です。

この問題は「関係を等式にしなさい」、なので形はいろいろあって良いです。

　\(\underline{a=5\,b+3}\)

または余りを等しくおいて、
　\(a-5\,b=3\)
でも良いでしょう。

(3)は代入問題ですが、\(\,x\,,y\,\)が与えられているからといって直接代入するような算数のようなことはやめましょう。

　\(\,x=\sqrt{3}+1\\
\,y=\sqrt{3}-1\,\)

のように数値が与えられている式を条件式といいます。

　\(\,xy+x\,\)

のように値を求める方の式を与式、または求値式といいます。

代入問題では与式をできるだけ簡単にしてから代入、を基本方針にしておきましょう。

　\(\hspace{10pt}xy+x\\
=x(y+1)\\
=(\sqrt{3}+1)(\sqrt{3}-1+1)\\
=(\sqrt{3}+1)\sqrt{3}\\
=\underline{3+\sqrt{3}}\)

因数分解した後
　\(\hspace{10pt}y+1\\
=\sqrt{3}-1+1\\
=\sqrt{3}\)
と、別に計算してから代入しても良いですよ。
もっとややこしい与式の場合は、それぞれの因数を別に計算して代入する方が楽な場合が多いです。

直接代入しても、
　\(\hspace{10pt}xy+x\\
=\color{red}{(\sqrt{3}+1)(\sqrt{3}-1)}+(\sqrt{3}+1)\\
=\color{red}{(\sqrt{3})^2-(1)^2}+(\sqrt{3}+1)\\
=(3-1)+\sqrt{3}+1\\
=2+\sqrt{3}+1\\
=3+\sqrt{3}\)
とたいした計算ではありませんが、
「計算すれば答えが出るから良い」、の算数は卒業しませんか？

難しくなればなるほど数学をやった方がだんぜんはやくなりますよ。

方程式の解と比例定数を求める問題

(4)は2次方程式です。

　「方程式を解きなさい。」
と
　「方程式の解を求めなさい。」
は同じことです。

⇒　方程式とは？方程式の解と移項とは？基本問題の解き方(中１数学)

2次方程式も同じです。

2次方程式を解く手順ですが、まずは因数分解を試して見ましょう。
文章題はほとんどの場合、出てきた方程式が2次方程式なら因数分解できます。
人数や個数に無理数はありませんからね。

小問集合では後が続かないので解の公式を使うことが多いのですが、ここではどうかはやってみないと分かりません。
思い込みはいけません。笑

解の公式を使えば2次方程式はすべて解けますが、時間がかかるので因数分解から試して見ましょう。

　\(x(x+4)=5\)

2次方程式はすべての項を左辺に集めることからです。

　\(\begin{eqnarray}
x(x+4)&=&5\\
x^2+4x&=&5\\
x^2+4x-5&=&0
\end{eqnarray}\)

定数項に着目します。
かけて\(\,-5\,\)になるのは

　\(\color{black}{\fbox{ (-1)×5 }}\)　か　\(\color{black}{\fbox{ 1×(-5) }}\)

しかありません。
このうち2つの数字を足して\(\,x\,\)の1次の係数\(\,+4\,\)になるのは
　
　\(\color{red}{\fbox{ (-1)×5 }}\)

なので左辺は
　\((x-1)(x+5)\)
と因数分解できるので

　\(\begin{eqnarray}　
x^2+4x-5&=&0\\
(x-1)(x+5)&=&0\\
x&=&\underline{1\,,\,-5}
\end{eqnarray}\)

(5)関数の1つ、反比例の比例定数を決める問題です。
求めるのは\(\,y\,\)座標ですが比例定数を決めなければ求まりません。

反比例の場合は、\(\,x,y\,\)の積は常に一定になるので、求める\(\,y\,\)座標を\(\,b\,\)として

　\(\,(-2)\times 3=(-4)\times b\,\)

という関係が成り立つので\(\displaystyle \,b=\frac{3}{2}\,\)

と求めることはできますが、飛んでいます。

比例でも反比例でも関数で座標を求めたいときは、関数を決定してからにしましょう。

　「\(\,y\,\)が\(\,x\,\)に反比例する」と問題にあれば
　\(\displaystyle \,y=\frac{a}{x}\,\)とおくことから始めます。

　\(\,(x,y)=(-2,3)\,\)
を通ることが表から分かるので代入します。

　\(\begin{eqnarray}
3&=&\frac{a}{-2}\\
-6&=&a
\end{eqnarray}\)

これで比例定数が決まりました。
関数は　\(\displaystyle y=\frac{-6}{x}\)　です。

この関数で\(\,x=-4\,\)のとき
　\(\begin{eqnarray}
y&=&\frac{-6}{-4}\\
&=&\underline{　\frac{3}{2}　}　(答え)
\end{eqnarray}\)

資料の活用(整理)と図形小問

(6)資料の活用（整理）は用語の意味を知らないと解ける問題はほとんどありません。

ここは「中央値」と「相対度数」です。

中央値とはデータを小さい（大きいでも同じ）順に並べたとき、
真ん中に位置する人の「値」です。（順番ではありません。）

例えば
　\(\,2,3,3,4,\color{red}{4},4,5,5,6\,\)
と\(\,9\,\)個のデータがあるときの中央値は、
真ん中\(\,5\,\)番目の\(\,4\,\)です。

　\(\,2,3,3,4,\color{red}{4,5},5,5,5,6\,\)
これはデータが\(\,10\,\)個（偶数個）ありますので真ん中に位置するデータがありません。
このときは真ん中\(\,2\,\)つの平均
　\(\displaystyle \frac{\color{red}{4+5}}{2}=4.5\)
が中央値になります。

この問題では\(\,40\,\)人のデータなので、
中央値は\(\,20\,\)番目の人と\(\,21\,\)番目の人のデータの平均が中央値になりますが、
中央値を聞いているのではありません。

中央値を含む階級の相対度数を聞いています。
上から数えても下から数えても良いですが、
\(\,20\,\)番目も\(\,21\,\)番目も「\(\,5\,\)冊以上\(\,10\,\)冊未満の階級」にあります。

「\(\,5\,\)冊以上\(\,10\,\)冊未満の階級」
の度数は\(\,10\,\)だから度数合計で割って
　\(\,(相対度数)=\displaystyle \frac{10}{40}=\underline{\frac{1}{4}=0.25}\,\)
相対度数は小数で答えることが多いですが、採点基準では分数も正解とする、となっていました。

(7)円すいの「側面積」を求める問題ですが、直接求める求める公式があります。

　母線の長さを\(\,\ell\,\)、底面の半径を\(\,r\,\)とすると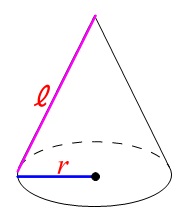
　\(\,\color{red}{側面積=\ell\,r\,\pi}\,　･･･①\)

これから求めるおうぎ形の面積は
　
　\(8\times 6\times \pi=\underline{48\pi} \)

使えるものはつかって良いです。
ただし、この公式は側面積を求めるときだけ使える公式なのでおすすめしません。

⇒　扇(おうぎ)形の面積を求める公式と弧の長さの求め方

理由を知りたい場合は確認しておいて下さい。

「展開図を書き」とわざわざ書いてくれているので展開図を書くと、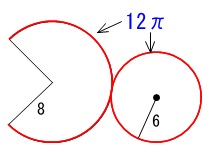

おうぎ形の弧と、底面の円周は等しいので
　\(2\times \pi \times 6=12\pi\)

ここからはおすすめする公式もあります。

　扇形の弧を\(\,\ell\,\)、半径を\(\,r\,\)とすると
　\(\,\displaystyle \color{blue}{扇形の面積=\frac{1}{2}\,\ell\,r}\,　･･･②\)

※
上の公式①と\(\,\ell,r\,\)の示している長さが違うので注意して下さい。

これから側面積は
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 8\times 12\pi\\
\underline{=48\,\pi}\)

何故？と思うのが普通です。
①の公式はおすすめではなく、②はおすすめなのか？

②は展開図を書いて作業した後で使う公式なので、表面積全体も出せます。
平面に変えているので展開図が応用問題にも対応します。

しかし、①は機械的すぎます。
先がない。
使うなといっているのではありませんよ。
公式は使って良いのですが、進学塾で詰め込まれた公式は作業がついてきていないので、
友達に教えてもらったちょっとした裏技的な公式を使うだけ、
というのはおすすめできません。

小問集合のちょっとした計算問題さえ取れれば良いのなら使って下さい。

もっというと側面積だけでなく表面積全体を求める公式もありますよ。

円すいの母線を\(\,\ell\,\)、底面の半径を\(\,r\,\)とすると、
　\(\,表面積=r\,(\,\ell\,+\,r\,)\,\pi\,\)

この公式覚えるヒマがあるなら展開図を書くクセをつけた方がいろいろと役に立ちますよ。

この問題は、展開図から中心角の比を利用するのが普通でしょう。

半径\(\,8\,\)の円周は\(\,16\,\pi\,\)です。
おうぎ形の弧の長さは\(\,12\,\pi\,\)です。

　\(\,16\,\pi\,\)のとき\(\,360°\,\)
　\(\,12\,\pi\,\)のときおうぎ形の中心角\(\,a\,\)は？

という比例式を立てればおうぎ形の中心角が求まります。
中心角は出さなくても面積は出ますが復習のつもりで出しておきます。

　\(\begin{eqnarray}
16\pi:360^{\circ}&=&12\pi:a\\
16\pi\times a&=&360^{\circ}\times 12\pi\\
\displaystyle a&=&\frac{360^{\circ}\times 12\pi}{16\pi}\\
&=&270^{\circ}
\end{eqnarray}\)

だから扇形の面積は

　\(\hspace{10pt}\displaystyle \pi \times (8)^2\times \frac{270}{360}\\
=\underline{48\,\pi}\)

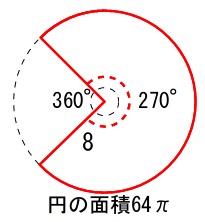円の面積を基準にして扇形の面積を求める方法です。

これは円の面積と中心角の比を利用していますが、
扇形の面積は弧の長さにも比例するので、

　\(\hspace{10pt}\displaystyle \pi \times 8^2\times \frac{12\pi}{16\pi}\\
=\underline{48\,\pi}\)
としても良いですよ。

(8)角度を求めるときは図の中で処理を終わらせておくことです。

見逃してはいけない条件は

　\(\,\mathrm{BD}\,\)が直径

ということです。

　直径に対する円周角は\(\,\mathrm{90°}\,\)

なのでこれを利用して下さい、とさりげなく与えられた条件です。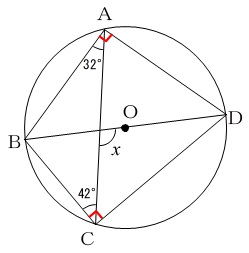このことと円周角の定理からすべての角度が分かります。

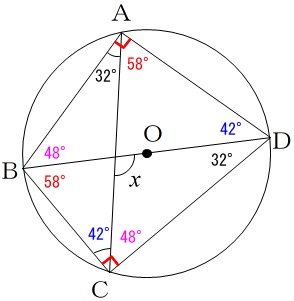
\(\,x\,\)を求める方法はいろいろありますので好きなものを使って下さい。

　\(x=\underline{100^{\circ}}\)

はやいのは、\(\,\mathrm{∠CAD=58^{\circ}}\,\)と出して、
同じ弧の円周角は等しいことから\(\,\mathrm{∠CBD=58^{\circ}}\,\)
と書き込んだ時点で
　\(\begin{eqnarray}
x&=&42^{\circ}+58^{\circ}\\
&=&100^{\circ}
\end{eqnarray}\)
とすることでしょうか。

どれも大して計算量は変わりませんが、図に角度を書き込んでいくというのは角度を求めるときには大きな違いとなります。