2018年青森県公立高校入試数学の過去問第3問の解説

青森県で2018年(平成30年度)に行われた公立高校入試の数学過去問第3問の解説です。
第3問は平面図形と空間図形の問題があります。
証明、角度、長さ、面積、体積、と図形全体を問われますが、
空間図形は平面図形の組み合わせでできているということを確認して下さい。

問題は青森県の公式サイトで公開してくれています。

⇒　青森県2018年公立高校入試数学問題

合同の証明と角度の求め方

\(\large{\color{black}{\fbox{　3　}}}\)　は図形総合問題です。

与えられた条件を確認しながら進めましょう。
ほとんどの問題は条件はすべて使わないと答えは出ませんよ。

(1)
ア

合同の証明ですが、この\(\color{black}{\fbox{　ア　}}\)のように、中に適する角度や辺を入れる問題では、
最初においた証明したい三角形を書いた時点で考えずに答えがうまります。

合同を示したい三角形は辺や角度が対応するように順番もそろえなくてはなりません。

\(\,\mathrm{△AEB}\,\)と\(\,\mathrm{△CDB}\,\)の合同であるなら、
記号の順番通り、\(\,\mathrm{∠A=∠C}\,\)や\(\,\mathrm{EB=DB}\,\)が対応する角や辺すべてで言えなくてはならないということです。

このことをちょっと頭の隅にでも置いておいて下さい。

問題に入りましょう。

問題にある条件です。

　\(\,\mathrm{△ABC}\,\)は正三角形
　点\(\,\mathrm{D}\,\)は\(\,\mathrm{△ABC}\,\)の内部にある
　\(\,\mathrm{△BDE}\,\)は正三角形
　\(\,\mathrm{△DCF}\,\)は正三角形
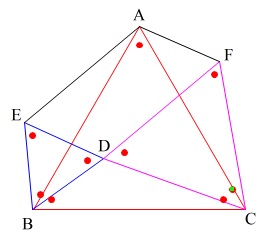正三角形の\(\,1\,\)つの角度\(\,60°\,\)が重なるので見にくくなっていますが自分で適当に見分けて下さい。

『［証明］
　\(\,\mathrm{△AEB}\,\)と\(\,\mathrm{△CDB}\,\)について』

とあります。

合同や相似の証明では
　\(\,\mathrm{△\color{red}{A}\color{blue}{E}\color{magenta}{B}}\,\)と\(\,\mathrm{△\color{red}{C}\color{blue}{D}\color{magenta}{B}}\,\)
の順に順番をそろえなくてはならないし、
　左に書いた三角形は左辺に、
　右に書いた三角形は右辺に、
書かなくてはなりません。

証明の続きを進めます。

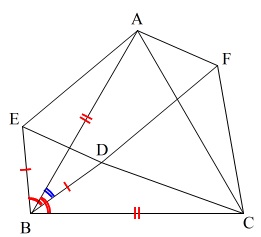
仮定より、
　\(\,\mathrm{AB}=\color{black}{\fbox{\(\,\mathrm{　\color{red}{CB}　}\,\)}}\,　･･･①\)
　\(\,\mathrm{BE=BD}　･･･②,\)

ここまでは順番通り入れれば図がなくても入ります。

　\(\,\mathrm{∠EBD=∠ABC}　･･･③\,\)
は正三角形の1つの内角なので等しい。

また、
　\(\,\mathrm{∠EBA=∠EBD-\color{black}{\fbox{\(\,　い　\,\)}}　･･･④}\,\)
　\(\,\mathrm{∠DBC=∠ABC-\color{black}{\fbox{\(\,　い　\,\)}}　･･･⑤}\,\)

となっていますが\(\,\mathrm{∠EBD}\,\)と\(\,\mathrm{∠ABC}\,\)は正三角形の1つの内角で等しく、
同じ\(\color{black}{\fbox{　い　}}\)（共通の角）を引いた角度なので等しいはずです。

共通になっているのは
　\(\,\color{black}{\fbox{　い　}}=\color{black}{\fbox{\(\mathrm{　\color{blue}{∠ABD}　}\)}}\,\)

後は合同条件です。

図で証明は済ませてあるのですぐに分かるでしょう。
　\(\color{black}{\fbox{　う　}}=\color{black}{\fbox{\(\,　\color{red}{2組の辺とその間の角}　\,\)}}\)

図の中で証明は示せておく、というのは証明のポイントになります。

イ
　『四角形\(\,\mathrm{AEDF}\,\)が正方形になるとき』

ここでは証明していませんが\(\,▱\,\)\(\,\mathrm{AEDF}\,\)は平行四辺形です。

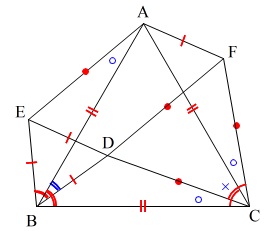
しかし必要ありません。
四角形\(\,\mathrm{AEDF}\,\)が正方形だとすれば、\(\,\mathrm{∠DBC}\,\)は求まります。

正方形はひし形であり、長方形です。
　\(\,\mathrm{\color{blue}{ED=DF}}\,\)
　\(\,\mathrm{\color{blue}{∠EDF=90^{\circ}}}\,\)

このことから

　\(\,\mathrm{\color{blue}{BD=DC}}\,\)

となり、\(\,\mathrm{△DBC}\,\)は二等辺三角形です。
※
\(\,\mathrm{△BDE}\,\)と\(\,\mathrm{△DCF}\,\)は合同な正三角形となります。
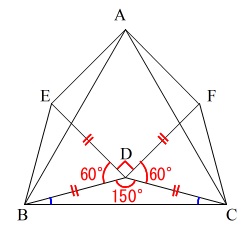説明はいらないでしょう。
二等辺三角形の底角は等しくなるので
　\(\begin{eqnarray}
\displaystyle \mathrm{∠BDC}&=&\frac{180^{\circ}-150^{\circ}}{2}\\
&=&\underline{　15^{\circ}　または　15度}
\end{eqnarray}\)

※
解答用紙に何が書いてあるかが分からないのですが、角度の単位はそろえておきましょう。
ちなみに\(\,15\,\)という「度」または「°」のついていない角度は度分法（度数法、六十分法）ではないので\(\,15\,\)だけだと間違いになります。
　

辺の長さと面積の求め方

(2)は正四面体です。
正四面体はすべての面が正三角形だということは思い出しておきましょう。

条件を書き出します。

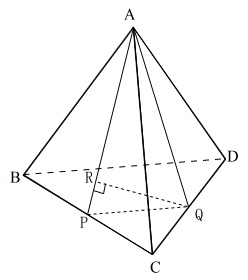
　\(\,1\,\)辺\(\,8の\,\)正四面体\(\,\mathrm{ABCD}\,\)
　\(\,\mathrm{P}\,\)は\(\,\mathrm{BC}\,\)の中点
　\(\,\mathrm{Q}\,\)は\(\,\mathrm{DC}\,\)の中点
　\(\,\mathrm{AP⊥QR}\,\)
　

ア
\(\,\mathrm{AQ}\,\)の長さです。
立体では長さを求めるとき、求めたい線分を含む面を抜き出します。
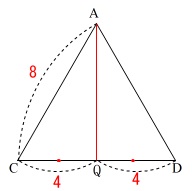\(\,\mathrm{△ACD}\,\)は正三角形で\(\,\mathrm{Q}\,\)は\(\,\mathrm{DC}\,\)の中点です。
三角定規の辺の比を利用して
　\(\begin{eqnarray}
1:\sqrt{3}&=&4:\mathrm{AQ}\\
\mathrm{AQ}&=&\underline{　4\sqrt{3}　}
\end{eqnarray}\)

でも良いですが、三平方の定理で確認しておきましょう。
　\(\begin{eqnarray}
\mathrm{AQ^2+CQ^2}&=&\mathrm{AC^2}\\
\mathrm{AQ^2}+4^2&=&8^2\\
\mathrm{AQ^2}&=&64-16\\
\mathrm{AQ^2}&=&48\\
\mathrm{AQ}&=&\pm 4\sqrt{3}
\end{eqnarray}\)

\(\,\mathrm{AQ}\,\)は長さなので\(\,\mathrm{AQ＞0}\,\)だから

　\(\,\mathrm{AQ=\underline{　4\sqrt{3}　}}\,\)

\(\,\mathrm{AQ^2}\,\)の平方根を求めるときは素因数分解をきっちりやってミスのないようにしましょう。

イ
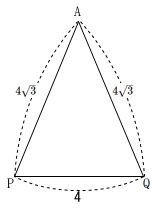
\(\,\mathrm{△APQ}\,\)の面積です。
やることは線分の長さを求めるときと同じです。
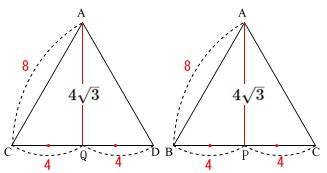\(\,\mathrm{AP}\,\)は\(\,\mathrm{AQ}\,\)と同じ長さです。
さらに、
　\(\,\mathrm{P,Q}\,\)はそれぞれ\(\,\mathrm{BC,DC}\,\)の中点
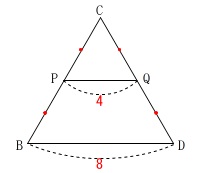なので中点連結定理から
　\(\displaystyle \mathrm{PQ=\frac{1}{2}BD=4}\,\)
ここで\(\,\mathrm{△APQ}\,\)を抜き出すと
面積を求めるので高さが必要です。
この二等辺三角形に\(\,\mathrm{A}\,\)から\(\,\mathrm{PQ}\,\)に垂線\(\,\mathrm{AM}\,\)を引きます。
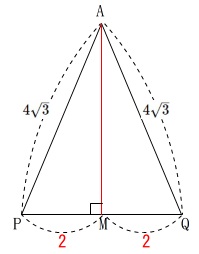三平方の定理から
　\(\begin{eqnarray}
\mathrm{AM^2+PM^2}&=&\mathrm{AP^2}\\
\mathrm{AM^2}+2^2&=&(4\sqrt{3})^2\\
\mathrm{AM^2}&=&48-4\\
\mathrm{AM^2}&=&44\\
\mathrm{AM}&=&2\sqrt{11}　（\mathrm{AM}＞0）
\end{eqnarray}\)

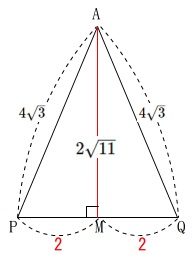
よって\(\,\mathrm{△APQ}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△APQ}&=&\frac{1}{2}\times \mathrm{PQ} \times \mathrm{AM}\\
&=&\frac{1}{2}\times 4 \times 2\sqrt{11}\\
&=&\underline{　\color{red}{4\sqrt{11}}　}　(\mathrm{cm}^2)
\end{eqnarray}\)

三角形や正四面体は転がしても面積は変わらない

ウ
\(\,\mathrm{QR}\,\)の長さを求める問題です。
\(\,\mathrm{△APQ}\,\)を抜き出します。

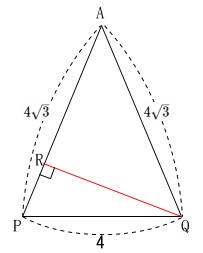
\(\,\mathrm{AR}\,\)か\(\,\mathrm{PR}\,\)を\(\,x\,\)とおいて三平方の定理を利用するということもできますが、イの問題の答えを利用しましょう。

三角形は回転させても面積は変わりません。
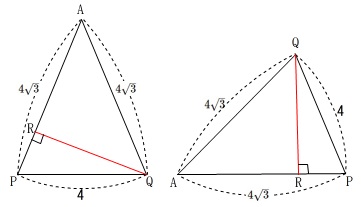底辺を\(\,\mathrm{AP}\,\)、高さを\(\,\mathrm{QR}\,\)と見ると\(\,\mathrm{△APQ}\,\)の面積を求めることができます。

イで\(\,\mathrm{△APQ}=\color{red}{4\sqrt{11}}\,\)と面積を求めているので
　\(\begin{eqnarray}　\displaystyle
\frac{1}{2}\times \color{blue}{\mathrm{AP}} \times \mathrm{QR}&=&\color{red}{4\sqrt{11}}\\
\frac{1}{2}\times \color{blue}{4\sqrt{3}}\times \mathrm{QR}&=&4\sqrt{11}\\
2\sqrt{3}\times \mathrm{QR}&=&4\sqrt{11}\\
\mathrm{QR}&=&\frac{4\sqrt{11}}{2\sqrt{3}}\\
&=&\frac{2\sqrt{11}}{\sqrt{3}}\\
&=&\underline{　\color{red}{\frac{2\sqrt{33}}{3}}　}
\end{eqnarray}\)

すべてとは言えませんが、(1)(2)(3)と続く問題では前問の答えを利用することが多いですよ。
問題の作成者が親切に誘導してくれているのです。

体積の比の求め方

(2)エ
この問題は『体積を求めなさい』ではありません。

もちろん具体的に体積を求めて比較しても良いのですが、何倍かを聞かれたら比を出して計算する方がはやいです。

簡単に言えば、基準になる立体の体積の圧縮、圧縮を繰り返していく方法です。

ただ、この体積比は、
　三角すい\(\,\mathrm{R\color{red}{BCD}}\,\)と三角すい\(\,\mathrm{A\color{red}{BCD}}\,\)
と底面\(\,\mathrm{\color{red}{BCD}}\,\)が同じで面積が等しいので、
　高さ1つだけの比
で答えが出ます。

実際には簡単に高さの比は出せますが少していねいに説明しておきます。

\(\,\mathrm{△BCD}\,\)を底面と見ると高さは
　\(\,\mathrm{A}\,\)から\(\,\mathrm{△BCD}\,\)に下ろした垂線
　\(\,\mathrm{R}\,\)から\(\,\mathrm{△BCD}\,\)に下ろした垂線
となります。

この垂線は正四面体の場合、中線\(\,\mathrm{DP}\,\)上に降ります。

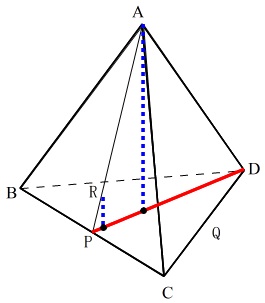\(\,\mathrm{△APD}\,\)を抜き出してみましょう。
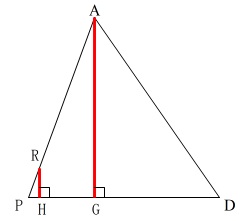この\(\,\mathrm{AG:RH}\,\)が高さの比でもあり、体積比にもなります。
\(\,\mathrm{G}\,\)は底面\(\,\mathrm{BCD}\,\)の重心に降りるので長さは求まりますが、
\(\,\mathrm{H}\,\)はどこにあるのかはすぐには分かりません。

そこで、相似の出番です。

　\(\,\mathrm{△PAG}\,\)　∽　\(\,\mathrm{△PRH}\,\)

は証明なしに分かるでしょう。
この相似な三角形において
　\(\,\mathrm{AG:RH=PA:PR=PG:PH}\,\)
なので
　\(\,\mathrm{AG:RH=PA:PR}\,\)
を利用します。

これはどの辺を利用しても同じなのですが、前問までに出している長さがあるので利用しやすいものを選んでいるだけですよ。
出てきた長さは図に書き込む、というのはやっておくべきことです。

長さの分かっている部分を書き込むと、
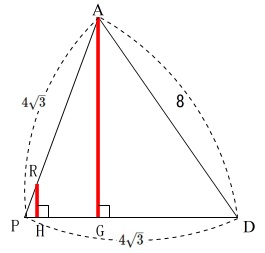\(\,\mathrm{AG}\,\)はすぐに求まるので\(\,\mathrm{PG}\,\)を求めても良いのですが、
\(\,\mathrm{PH}\,\)の長さを求める糸口がすぐには見つかりません。

そこで前問までを見ると、\(\,\mathrm{PR}\,\)は直角三角形\(\,\mathrm{△PQR}\,\)の\(\,1\,\)辺です。
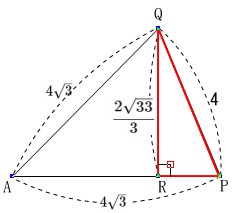直角三角形\(\,\mathrm{PQR}\,\)に三平方の定理を用いると
　\(\begin{eqnarray}
\mathrm{PR^2+QR^2}&=&\mathrm{PQ^2}\\
\mathrm{PR^2}+\left(\frac{2\sqrt{33}}{3}\right)^2&=&4^2\\
\mathrm{PR^2}+\frac{4\times 33}{9}&=&16\\
\mathrm{PR^2}&=&16-\frac{4\times 33}{9}\\
&=&\frac{16\times 9-4\times 33}{9}\\
&=&\frac{4(36-33)}{9}\\
&=&\frac{4\times 3}{9}\\
\mathrm{PR}&=&\frac{2\sqrt{3}}{3}　（\mathrm{PR}＞0）
\end{eqnarray}\)

※
この計算は
　\(\begin{eqnarray}
\mathrm{PR^2}&=&16-\frac{4\times 33}{9}\\
&=&\frac{16\times 9-4\times 33}{9}\\
&=&\frac{144-132}{9}\\
&=&\frac{12}{9}\\
\mathrm{PR}&=&\frac{2\sqrt{3}}{3}
\end{eqnarray}\)
で良いです。
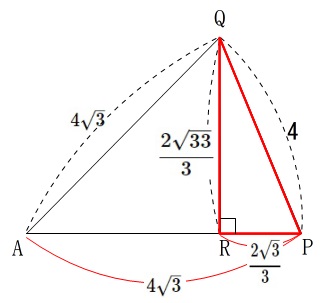これで高さの比がでます。

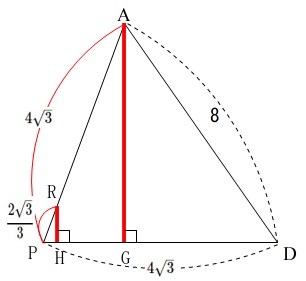
　\(\begin{eqnarray}
\mathrm{AG:RH}&=&\mathrm{AP:PR}\\
&=&4\sqrt{3}:\frac{2\sqrt{3}}{3}\\
&=&4:\frac{2}{3}\\
&=&12:2\\
&=&6:1
\end{eqnarray}\)

底面積が同じで、高さの比が\(\,6:1\,\)でなので
　三角すい\(\,\mathrm{ABCD}\,\)の体積\(\,\mathrm{【ABCD】}\,\)
と
　三角すい\(\,\mathrm{RBCD}\,\)の体積\(\,\mathrm{【RBCD】}\,\)
の比は
　\(\hspace{10pt}【\mathrm{ABCD}】：【\mathrm{RBCD}】\\
=　　　6　　:　　1\)

よって　\(\displaystyle \underline{　\color{red}{\frac{1}{6}　倍}　}\)　

\(\,\mathrm{A,R}\,\)からの垂線が\(\,\mathrm{PD}\,\)に降りることから\(\,\mathrm{△APD}\,\)を抜き出しましたが、
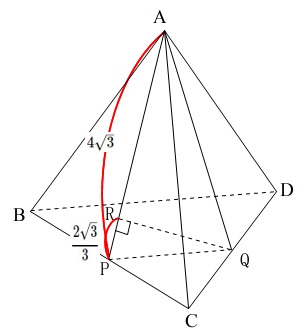この状態が書けた時点で、線分比と体積比が出せるくらいの練習をしておくと良いですね。