2018年(平成30年)度青森県公立高校入試過去問の数学第4問の解説

2018年(平成30年)度に青森県で行われた公立高校入試過去問の数学第4問の解説です。
第4問は関数のグラフを書く基本問題から動点の表す関数のよくある問題です。
動点問題のポイントをこの問題で確認しておくと良いですよ。

問題は青森県の公式サイトで公開してくれています。

⇒　青森県2018年公立高校入試数学問題

数学が苦手な人の関数への勘違い

\(\large{\color{black}{\fbox{　4　}}}\)　は関数です。
動点問題を図形の問題と思っている人がいますが、どう見ても関数問題です。

関数が教科書のようにグラフまでと勘違いしないでください。
関数はすべての項目に関わってきます。
この問題のように動点（動く点）と面積の関係が関数になるように、
ほとんどの関係は関数になるということを知っておくと良いです。

関数とは

関数の定義をここで確認しておきます。

中学生の関数の定義では、もう少し狭い範囲で定義します。

よく読めば2つの変数を決めるとほとんどの関係が関数になることが分かるでしょう。
分かりませんか？

では関数の問題を解いて行きましょう。

(1)『グラフを書きなさい。』、という本当なら自分でやらなければいけないことを問題にしてくれています。

グラフを書くというのは定期テストの問題になるだけではありませんよ。
問題になっていなくても関数問題はすべてグラフを書いて考えると分かり易くなります。

　\(\displaystyle y=\frac{1}{2}x^2\)

このグラフは原点を通る放物線になります。

　比例定数が正のとき下に凸な（上に開いている）グラフ
　比例定数が負のとき上に凸な（下に開いている）グラフ

この関数は比例定数が正なので下に凸なグラフです。
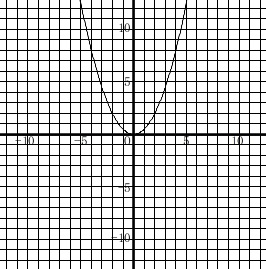自分で確認のために書くのはこれくらいで良いです。
しかし、『グラフを書きなさい。』という問題ではもう少し正確に通る点を示しましょう。

このグラフは正確ですよ。
ただ、手書きだと怪しい点が出てきますのでどこの点を通ったなめらかな曲線かをはっきりと示した方が良いです。

※
曲線は直線を含みます。

⇒　直線は曲線の1つ

　\(\displaystyle y=\frac{1}{2}x^2\)上の点をいくつか示します。

　\(\displaystyle \left(\,1\,,\,\frac{1}{2}\,\right)\),\((\,2\,,\,2\,)\),\(\displaystyle \left(\,3\,,\,\frac{9}{2}\,\right)\),\((\,4\,,\,8\,)\),\(\displaystyle \left(\,5\,,\,\frac{25}{2}\,\right)\)

これらがその値の整数と整数の間の区間を通っているようにできるだけ正確に示すと良いです。
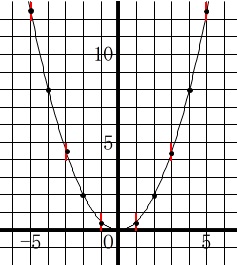赤い線は書かなくても良いですが、
赤い線の間を通るようにすることと、点は必ず通るようにグリグリ黒丸にすると多少のズレは正解となる範囲です。
原点もしっかり黒く●しておくと原点を通っていることをアピールできます。
（よく見たらグラフの点が多少ずれてますね。本当は赤線の中点です。）

グラフはすべて点の集まりだということを忘れなければ必ず書けます。
いくつか点を取って結べば良いのですよ。

たかがグラフ1つ書くのにどれだけしつこい説明してんだよ！
と思ったでしょう？

グラフを書かないから値域問題を間違えるんです。
グラフを書いて確認しないから定義域が答えられないのです。

『間違えたくないならグラフ書けば？』

って考えているのは出題者も同じだと思いますよ。
これを単なる過去問解説だと思っている人はスルーして良いです。

次行きます。

動点問題の注意点とポイント

(2)正方形の辺上を2つの点が動きます。

こういった図形上を点が動く問題は多いですが、

　ポイント：具体的な点をいくつか書いてみること
　注意点　：点の動きが変化するところを境に見方を変える

ということだけです。
要は図を細かく書き分ければ良いだけなのですが、やらない人が多いです。
数学の問題は、手を前で組んでいても解決しない場合が多いですよ。

まずは、条件となる正方形と\(\,2\,\)点\(\,\mathrm{P,Q}\,\)の動き方を知っておきましょう。
単位は省略します。

　正方形\(\,\mathrm{ABCD}\,\)は\(\,1\,\)辺が\(\,6\,\)
　\(\,\mathrm{P}\,\)は\(\,\mathrm{A→B→C→D}\,\)の順に毎秒\(\,1\,\)の速さで動き\(\,\mathrm{D}\,\)で止まる。
　\(\,\mathrm{Q}\,\)は\(\,\mathrm{A→D}\,\)の順に毎秒\(\,1\,\)の速さで動き\(\,\mathrm{D}\,\)で止まる。

さらに変数も指定されています。

　\(\,\mathrm{P,Q}\,\)が\(\,\mathrm{A}\,\)を出発してからの時間を\(\,x\,\)秒
　\(\,\mathrm{△APQ}\,\)の面積を\(\,y\,\)とする。

この変数\(\,x,y\,\)が何を表しているかを理解していないとすべての関数問題は解けません。

では問題に入る前にいくつか点を見ておきましょう。
\(\,3\,\)秒後の状態です。

\(\,\mathrm{P,Q}\,\)ともに\(\,3\,\)動くので\(\,\mathrm{P}\,\)は\(\,\mathrm{AB}\,\)上に、\(\,\mathrm{Q}\,\)は\(\,\mathrm{AD}\,\)上にあります。

\(\,\mathrm{△APQ}\,\)は底辺\(\,\mathrm{AP}\,\)、高さ\(\,\mathrm{AQ}\,\)なので\(\,\mathrm{△APQ}\,\)の面積は
　\(\begin{eqnarray}
\displaystyle \mathrm{△APQ}&=&\frac{1}{2}\times 3\times 3\\
&=&\frac{9}{2}
\end{eqnarray}\)

となります。

\(\,2\,\)点\(\,\mathrm{P,Q}\,\)ともに速さは秒速\(\,1\,\)なので
　\(\,\mathrm{P}\,\)は\(\,\mathrm{A→B}\,\)で\(\,6\,\)秒
　\(\,\mathrm{Q}\,\)は\(\,\mathrm{A→D}\,\)で\(\,6\,\)秒
かかることになります。

つまり\(\,6\,\)秒後までは
　\(\,\mathrm{P}\,\)は\(\,\mathrm{AB}\,\)上に
　\(\,\mathrm{Q}\,\)は\(\,\mathrm{AD}\,\)上に
あります。

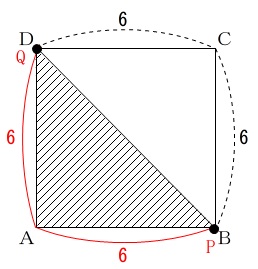
この\(\,6\,\)秒後が変化の境です。

この後、
\(\,\mathrm{P}\,\)は\(\,\mathrm{BC}\,\)上を動きますが、
\(\,\mathrm{Q}\,\)は\(\,\mathrm{D}\,\)に止まったままです。

これが読み取れればこの問題は終わりです。

ところで、
\(\,6\,\)秒後までは\(\,\mathrm{△APQ}\,\)は底辺\(\,x\,\)、高さ\(\,x\,\)の三角形なので
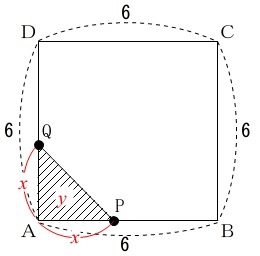\(\,\mathrm{△APQ}\,\)の面積\(\,y\,\)は
　\(\begin{eqnarray} \displaystyle
y&=&\frac{1}{2}\times x\times x\\
&=&\frac{1}{2}x^2
\end{eqnarray}\)

ここまで問題に書いてくれている親切な問題です。

では問題を解いていきましょう。

ア
変化の割合です。

　\(\,\displaystyle \color{red}{(変化の割合)=\frac{　(\,x\,の増加量\,)　}{　(\,y\,の増加量\,)　}}\,\)

忘れている人がいれば教科書で確認しておいて下さい。

関数\(\,\displaystyle y=\frac{1}{2}x^2\,\)について、\(\,x\,\)の値が\(\,2\,\)から\(\,6\,\)まで増加するときの変化の割合を求めます。

\(\,1\,\)次関数を傾きを求めるときと同じように、2つの座標を書き出すと変化の割合はすぐにでます。

　\(\,x=2\,\)のとき\(\displaystyle \,y=\frac{1}{2}\times (2)^2\,=\,2\,\)
　\(\,x=6\,\)のとき\(\displaystyle \,y=\frac{1}{2}\times (6)^2\,=\,18\,\)
なので
　\(\,(\,\color{red}{2}\,,\hspace{6pt}\color{blue}{2}\,)\,\)
　\(\,(\,\color{red}{6}\,,\,\color{blue}{18}\,)\,\)

　\(\,x\,\)の増加量は\(\,x\,\)座標の差
　\(\,y\,\)の増加量は\(\,y\,\)座標の差
で、どちらから引いても良いですが、両方の座標とも同じ方向に引かなければ変化の割合の符号が逆になります。

下から上を引くと決めておくと良いです。

　\(\begin{eqnarray}\displaystyle
　(変化の割合)&=&\frac{\color{blue}{18}-\color{blue}{2}}{\color{red}{6}-\color{red}{2}}\\
&=&\frac{16}{4}\\
&=&\underline{　\color{red}{4}　}
\end{eqnarray}\)

イ
『\(\,x=14\,\)のとき\(\,y\,\)の値』を求めます。

つまり、
　\(\,14\,\)秒後の\(\,\mathrm{△APQ}\,\)の面積です。

\(\,14\,\)秒後の位置は、
　\(\,\mathrm{P}\,\)は\(\,\mathrm{A→B→C}\,\)まで\(\,12\,\)秒かかりさらに\(\,\mathrm{D}\,\)に向けて\(\,2\,\)秒進む
　\(\,\mathrm{Q}\,\)は4秒後以降は\(\,\mathrm{D}\,\)に止まったまま
なので
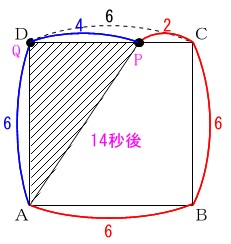この図を書けば良いだけです。
\(\,y\,\)は\(\,\mathrm{△APQ}\,\)の面積なので
　\(\begin{eqnarray}
y&=&\frac{1}{2}\times 6\times 4\\
&=&\underline{　\color{red}{12}　}
\end{eqnarray}\)

図を書くためのスペースはたくさん用意してくれています。

これを関数\(\displaystyle y=\frac{1}{2}x^2\)の\(\,x\,\)に\(\,14\,\)を代入した人は、場合ごとの図は書いていないことが分かるし、問題の意味を何も読み取れていないということです。

関数は変化のある
　①　\(\,0≦x≦6\,\)
　②　\(\,6≦x≦12\,\)
　③　\(\,12≦x≦18\,\)
で変わってきます。

ウはそれをそれぞれ関数で表しなさいという問題です。
　①　\(\,0≦x≦6\,\)のとき
　
これは問題に書かれているとおりで、点\(\,\mathrm{P}\,\)は\(\,\mathrm{AB}\,\)上にあって底辺、高さとも\(\,x\,\)で
　\(\displaystyle y=\frac{1}{2}x^2　(\,0\,≦\,x\,≦\,6\,)\)

　②　\(\,6≦x≦12\,\)のとき

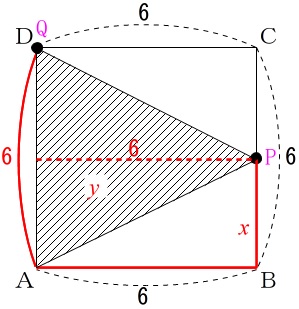
点\(\,\mathrm{Q}\,\)は\(\,6\,\)秒過ぎているので\(\,\mathrm{D}\,\)に止まっていて、
点\(\,\mathrm{P}\,\)は\(\,\mathrm{A}\,\)を過ぎて\(\,\mathrm{BC}\,\)の間にあります。

\(\,\mathrm{BC}\,\)間では\(\,\mathrm{△APQ}\,\)の底辺を\(\,\mathrm{AD}\,\)と見ると高さとなるのは\(\,\mathrm{AB}\,\)と同じで\(\,6\,\)で一定です。
　\(\begin{eqnarray}
y&=&\frac{1}{2}\times 6\times 6\\
&=&18　(\,6\,≦\,x\,≦\,12\,)
\end{eqnarray}\)

　③　\(\,12≦x≦18\,\)のとき
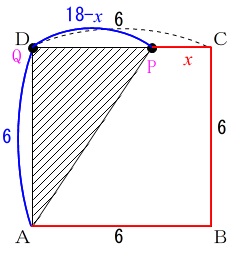点\(\,\mathrm{P}\,\)は\(\,\mathrm{DC}\,\)上にあります。

②のときは説明が必要無かったのでしませんでしたが、
角を曲がったとしても\(\,x\,\)秒で移動した長さは\(\,x\,\)です。

点\(\,\mathrm{P}\,\)は\(\,\mathrm{A→B→C→D}\,\)まで移動するには\(\,18\,\)秒かかりますが,

そのうち\(\,\mathrm{A→B→C→P}\,\)で\(\,x\,\)秒移動しているので、
残りの\(\,\mathrm{PD}\,\)は\(\,\color{blue}{(18-x)}\,\)となっています。

これを\(\,\mathrm{△APQ}\,\)の高さとして表せるかが大きなポイントになりますね。

点\(\,\mathrm{Q}\,\)は\(\,\mathrm{D}\,\)のままです。

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 6\times (18-x)\\
&=&3(18-x)　　(\,12\,≦\,x\,≦\,18\,)
\end{eqnarray}\)

①②③から\(\,\mathrm{△APQ}\,\)の面積、つまり\(\,y\,\)が\(\,16\,\)となるのは①か③のときだと分かります。
(②のときは\(\,y=18\,\)で一定なので\(\,y=16\,\)となるときはありません。）

必要ありませんがグラフで確認しておきましょう。
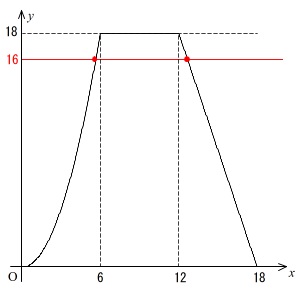直線\(\,y=16\,\)と交点となる点の\(\,x\,\)座標が求める\(\,x\,\)です。
2つあることが分かりますが、①と③のときです。

答えを出しておきます。

①のとき
　\( \begin{cases}\displaystyle
\hspace{7pt} y=\frac{1}{2}x^2\\ \\
\hspace{7pt} y=16
\end{cases}\)
から
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}x^2&=&16\\
x^2&=&32\\
x&=&\color{red}{4\sqrt{2}}　(x＞0)
\end{eqnarray}\)

『交点』　\(\,\Leftrightarrow\,\)　『連立』
です。

もう一つ、③のとき
　\( \begin{cases}\displaystyle
\hspace{7pt} y=3(18-x)\\ \\
\hspace{7pt} y=16
\end{cases}\)
から
　\(\begin{eqnarray}\displaystyle
3(18-x)&=&16\\
54-3x&=&16\\
-3x&=&16-54\\
3x&=&38\\
x&=&\color{red}{\frac{38}{3}}
\end{eqnarray}\)

答えは　\(\displaystyle \,\underline{　x=\color{red}{4\sqrt{2}}\,,\,\color{red}{\frac{38}{3}}　}\,\)　の2つです。

動点問題では変化する時間を境にそれぞれ図示する、というお話でした。

ここでは関数のグラフを書くという問題にはなっていませんが、
グラフをつなげて書く問題も多いのでグラフを書けるようになっておくと良いですね。

⇒　2018年(平成30年)度青森県公立高校入試過去問の数学第5問の解説

\(\large{\color{black}{\fbox{　5　}}}\)　は日本語がずらりと並んだ、読み取りに苦労する問題になります。

⇒　青森県公立高校入試2018数学の過去問と解説

\(\large{\color{black}{\fbox{　1　}}}\)　の小問集合を確実にとり、

⇒　2018年青森県公立高校入試数学の過去問第3問の解説

\(\large{\color{black}{\fbox{　3　}}}\)と\(\large{\color{black}{\fbox{　4　}}}\)までを素早く処理して7割を取っておくと最終問題にじっくり時間をかけて取り組めます。