正の数負の数 整数と自然数の違いは何？０は偶数、奇数どっち？

正の数負の数の単元にある整数と自然数ですが似ているけど違いがあります。
０は正の数負の数のどちらでしょう？また偶数なのか奇数なのか？
小学生の頃から知っている整数ですが、高校でもという単元が独立しているように奥は深く数の世界を知る上で重要な単元になります。
しかし、むずかしく考えなくても大丈夫です。
中学の間はその基本にしか触れませんので感覚でいいので理解しておきましょう。

整数と自然数との違い

「整数」と「自然数」という言葉の意味を改めてお伝えしておきます。

小学生の頃から、整数、分数、小数という言葉は聞いているとおもいますが、
その中でも、「整数」と「自然数」との違いをはっきりと見直しておきましょう。

たとえば、
－３，－１，０，１，５，１０
などの数を整数と言います。

小学校では「負の数」を習わないので－３などは知らなかっただろうけど今は知っていますよね。

このうち、
０より大きい整数
つまり１以上の整数を自然数といいます。

「より」という言葉はその数を含みません。
「以上」「以下」はその数を含みます。

注意するのは、
　０は整数だけど自然数ではない
ということです。

だから１，５，１０は自然数だけど整数でもあるわけです。

0は奇数か偶数か？

奇数とは
　\(\,2\,\)で割ったときに余りが\(\,1\,\)の数

偶数とは
　\(\,2\,\)で割ったとき余りが\(\,0\,\)の数

なので、

　\(\color{red}{\fbox{　0　は偶数}}\)

です。

整数と自然数の関係

関係を図に示すと、

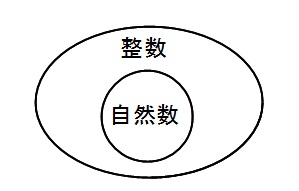
となっています。

見たら分かるように整数の中に自然数があって、
「整数の方が範囲が広い」
ということです。

では、整数と自然数が区別できるようになったところで、問題に入りましょう。

※問題６となっていますが、
問題５までは別のページにありますのでここにはありません。

（自然数）－（自然数）がいつも自然数か？

注目するのは「いつも」という言葉です。
「つねに」と書かれる場合もありますが同じ意味ですよ。

「いつも」「常に」の意味

「いつも」というのは、
自然数にならない場合が１つでもあってはダメなんです。

たとえば、
　３－２＝１　の場合、
３も２も自然数で答えの１も自然数ですが、
　２－３＝－１　の場合は、
２も３も自然数ですが答えが自然数ではない整数です。

このように、いつも自然数になるとは限らないので、
『成り立たない』となります。
（成り立たない例を、『反例』と言いますが用語としてはまだ扱いません。）
1つでも成り立たないものがあってはダメなんです。

ただ、先ほども書きましたが、－１ は整数ではあります。

つまり、
（整数）－（整数）＝（整数）
はいつも成り立つのです。

　\( 4-3=1\)

　\( 3-4=-1\)

負の数も整数ですからね。

いくつでも試して見てください。
必ず整数になりますから。

問題（１）は引き算（差）について見ていますが、
足し算（和）の場合は、
（自然数）＋（自然数）＝（自然数）
はいつも成り立ちます。

ということは、
（整数）＋（整数）＝（整数）
も、つねに成り立つということです。

（１）のように成り立たないものを探し出してみれば良いのでこの問題は簡単です。

たとえば、
　\(\,6 \div 2=3\,\)
と
　\(\,（整数）\div（整数）=（整数）\,\)
になりますが、

　\( 3\div 6\)

は整数になりません。

　\(\displaystyle 3\div 6=\frac{1}{2}=0.5\)

と分数、小数になります。
１つでもダメな場合があるときは「いつも」とは言えません。
答えは、『成り立たない』です。

『いつも』『つねに』という言葉が出てきたら、いくつか試して見れば良いだけです。

ただし、
都合の良いように試すのではなく、
すべてで成り立つのか、成り立たなさそうなものも探して、ですよ。

成り立つかどうかを示さなければならない訳ではないので、
成り立たない場合（反例）を探し出すだけで良いですよ。

問題によっては、
○や△といった記号で問題が出されるので、
整数や自然数をあてはめてください。

　「○や△は自然数とします。○－△はいつも自然数になるか。」
　「\(\,a\,\)と\(\,b\,\)を整数とするとき、\(\,a\div b\,\)はいつも整数といえるか。」
みたいに。
答えは、
　『ならない。反例：２－４＝－２』
　『いえない。反例：\(\,2\div 5=0.4\,\)』

難しく考えず、例をたくさんあげて見る、です。（これ大事！）

⇒　正の数負の数で分数計算が混じった加減乗除の練習問題とポイント

ここまでで正の数と負の数の計算もだいたい分かってきたでしょう。

⇒　文字と数式の表し方と×や÷の省略の仕方と計算順序

先に進んで数学の入り口を開けましょう。