正の数と負の数の分数も混じった計算と加減乗除の総復習を練習問題の中で解説します。
足し算引き算とかけ算わり算の順序の解説ですが、わり算、分数を含む問題からになります。
中学2，3年になって、高校に進んでも計算の順序や方法は変わりませんので算数の続きみたいな方法から卒業しておきましょう。
正の数負の数で分数が混じった計算のポイント
正の数負の数において加減（足し算、引き算）や
乗除（掛け算、割り算）はそれぞれできるできるでしょう。
ここでは分数の含め加減乗除が混じった計算のポイントになります。
ポイントは２つ、
・加減よりも乗除が先
・分数の割り算は逆数の掛け算
であることです。
文字式になっても変わりませんので
しっかり覚えておきましょう。
加減乗除の混じった計算練習問題
加法（足し算）減法（引き算）乗法（掛け算）除法（割り算）の、
分数も混じったまとめになりますので、
それぞれの計算はできているものとして、さっそくですが問題です。
（６）\( 12\div 3 \times 2-15\)
（７）\( 0.6+0.4\times (-7)\)
（８）\( (2.8-6.58)\div 0.7\)
（９）\(\displaystyle \frac{5}{8}-\frac{1}{6} \div \frac{2}{9}\)
（１０）\(\displaystyle \frac{1}{2}\times (-\frac{1}{3})-\frac{1}{2} \div 3\)
※
問題５となっていますが、問題４まではこのページにはありません。
計算が途切れるところ
－１５の「－」で計算が途切れます。
この「－」はマイナスという符号ではなく、「引く」という計算を表します。
割り算が出てくるけど逆数にするまでもありませんね。
\(\hspace{10pt} 12\div 3 \times 2-15\\
=4 \times 2-15\\
=8-15\\
=-7\)
暗算は自分の現状でできる最低限にしておきましょう。
練習のための暗算は良いですが、
テストでは出来るだけ暗算をさけて、
確実に、計算ミスを減らすようにしましょう。
計算順序の確認
＋０.４の前の＋で計算が途切れます。
かけ算部分の \( 0.4\times (-7)\) が先です。
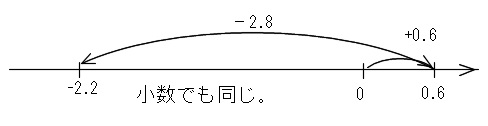
\(\hspace{10pt} 0.6+0.4\times (-7)\\
=0.6+(-2.8)\\
=0.6-2.8\\
=-2.2\)
計算は途切れませんが（ ）の中からの処理ですね。
計算は数直線上で慎重にやりましょう。
分数に直しての計算も出来ますがこれは小数のまま進めます。
\(\hspace{10pt} (2.8-6.58)\div 0.7\\
=(-3.78)\div 0.7\\
=-(3.78\div 0.7)\\
=-5.4\)
\(3.78\div 0.7\) の計算があやしい人は算数の割り算の計算練習をもっとやってください。
筆算で良いのですよ。暗算できるけど間違えたくないので私は筆算します。
長くなりすぎるのでここではやりません。
小数の割り算がむちゃくちゃ苦手な人は分数の計算を得意にして下さい。
\(\hspace{10pt} 3.78\div 0.7\\
\displaystyle =\frac{3.78}{0.7}\\
\displaystyle =\frac{378}{70} （\color{red}{ここで筆算でも良い}）\\
\displaystyle =\frac{189}{35}\\
\displaystyle =\frac{27}{5}\\
=5.4\)
割り算を分数に変えて小数点を無くし、約分できる数を簡単なものから見つけて約分を繰り返しているだけです。
答えを小数にするか分数にするかですが、同じ数を表しているのでどちらも同じですよ。
数学では分数がほとんどですが、資料の整理（活用）の相対度数など、分野によっては小数を使います。
割り算と通分の基本
割り算は逆数のかけ算に替えるんですよ。
\(\hspace{10pt} \displaystyle \frac{5}{8}-\displaystyle \frac{1}{6} \div \displaystyle \frac{\color{red}{2}}{\color{blue}{9}}\\
=\displaystyle \frac{5}{8}-\displaystyle \frac{1}{6} \times \displaystyle \frac{\color{blue}{9}}{\color{red}{2}}\\
=\displaystyle \frac{5}{8}-\displaystyle \frac{3}{4}\)
通分ですが、分母は１つに、ですよね？
\(\hspace{10pt}\displaystyle \frac{5}{8}-\frac{3}{4}\\
\displaystyle=\frac{5-3\times 2}{8}\\
\displaystyle=\frac{5-6}{8}\)
\(\displaystyle =\frac{-1}{8} または -\frac{1}{8}\)
分数の－は分子か、分数全体の前につけてください。
分母に－をつけたまま、答えにしないでくださいね。
練習問題の最後です。
計算が途切れるのはどこか分かりますか？
ここまでがしっかり定着していれば出来るはずですので、自力でやって見てください。
\(\hspace{10pt} \displaystyle \frac{1}{2}\times (-\displaystyle \frac{1}{3})-\displaystyle \frac{1}{2} \div 3\\
=-\displaystyle \frac{1\times 1}{2\times 3}-\displaystyle \frac{1\times 1}{2\times 3}\\
=-\displaystyle \frac{1}{6}-\displaystyle \frac{1}{6}\\
=\displaystyle \frac{-1-1}{6}\\
=\displaystyle \frac{-2}{6} =-\displaystyle \frac{1}{3}\)
いきなり答えにしても良いのですが、ていねいに計算してみました。
間違っても
\( -\displaystyle \frac{1}{6}-\displaystyle \frac{1}{6}=0\)
なんていうミスはしないようにしっかり分子の計算に持ち込んでくださいね。
ここまでで、正と負の数の計算の基本は一通りやったことになります。
算数の延長みたいなところなので分数計算があやしい人は、
分母を１つにして、分子の計算に専念する、という方法にこの際に変えてみてください。
きっと数学で通用するようになります。
計算方法が1つに思えるようになれば文字式の計算に進んで大丈夫です。
計算力に不安がある人も文字式の計算を数学らしく続ければ、数学に必要な計算力はついてきますよ。
時間に余裕があるときに足し算引き算の基本からやり直しておくと良いです。
整数と自然数の性質についてお伝えするのを忘れていました。
⇒ 正の数負の数 整数と自然数の違いは何？０は偶数、奇数どっち？
整数の奥は深いですが、中学生はそれほど難しく考えなくて良いです。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
