2018(H30)年度秋田県公立高校入試数学の過去問第3問の解説

秋田県で2018年(平成30年度)に行われた公立高校入試の数学の過去問（第3問）の解説です。
この一般選抜試験の問3は平面図形総合問題になります。
合同の証明、相似の証明、面積比がありますが短時間で処理できますので基本の確認をしておくと良いです。

問題は秋田県の公式サイトにもあります。

⇒　2018年秋田県公立入試数学過去問

　\(\,\large{3}\,\)

条件の確認

問題が(1)(2)(3)とありますが、すべての問題に共通する条件があります。
問題で(1)から続いて問題がある場合は、
その前にある条件は問題全体に通じる条件ですので忘れないようにしておきましょう。

ただし、(1)(2)(3)ではそれぞれ条件が加わることもありますが、その問題だけの条件の場合もあるので問題はよく読んで下さい。

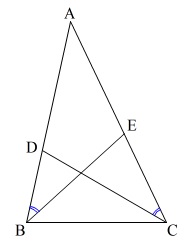
全体に通じる条件です。

　\(\color{black}{\fbox{　条件　}}\)

　\(\,\mathrm{△ABC}\,\)において\(\,\mathrm{D,E}\,\)はそれぞれ\(\,\mathrm{AB,AC}\,\)上にある。

　\(\,\mathrm{\color{blue}{∠ABE=∠ACD}}\,\)

特別な条件の場合

(1)
美咲さんは\(\,\mathrm{AB=AC}\,\)の場合を考えます。

このとき\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ACD}\,\)が合同であることを証明します。

合同でも相似でも証明を書く前に図の中で証明を示せておくのが先ですよ。

図の中で示せていないものが、証明になるはずありません。

合同の証明のときに気をつけるのは、

　\(\,\mathrm{△\color{red}{A}\color{blue}{B}E}\,\)と\(\,\mathrm{△\color{red}{A}\color{blue}{C}D}\,\)において

と書きだしたら、
　左辺には左に書いた\(\,\mathrm{△\color{red}{A}\color{blue}{B}E}\,\)について
　右辺には右に書いた\(\,\mathrm{△\color{red}{A}\color{blue}{C}D}\,\)について
書き並べるということと、
　記号の順番もそろえる
ということです。

例えば、
　\(\,\mathrm{\color{red}{A}E=\color{red}{A}D}\,\)
を
　\(\,\mathrm{\color{red}{A}E=D\color{red}{A}}\,\)
とはしないということです。

［証明］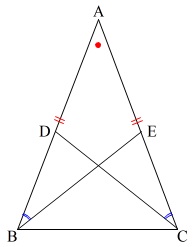
　\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ACD}\,\)において、

　　\(\,\mathrm{AB=AC}\,\)　（仮定）
　　\(\,\mathrm{∠ABE=∠ACD}\,\)　（仮定）
　　\(\,\mathrm{∠BAE=∠CAD}\,\)　（共通）
よって
　1組の辺とその両端の角がそれぞれ等しい
ので
　\(\,\mathrm{△ABE}　≡　\mathrm{△ACD}\,\)
（終わり）

条件の変化（条件の一般化）

(2)
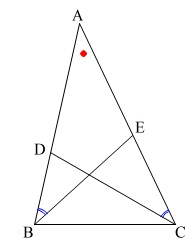
健司さんは\(\,\mathrm{AB}\,\)と\(\,\mathrm{AC}\,\)の長さが異なるときに、

　\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ACD}\,\)がどういう関係になるか

を考えています。

(1)で共通角として取り上げた

　\(\,\mathrm{∠BAE=∠CAD}\,\)

は\(\,\mathrm{AB}\,\)と\(\,\mathrm{AC}\,\)の長さが異なるときでも言えるので、

　\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ACD}\,\)は、
　\(\color{black}{\fbox{\(\,\color{red}{　必ず相似になります。　}\,\)}}\)

このことは次の誘導になるかもしれないのでしっかり書き出しておきましょう。

　\(\,\mathrm{△ABE}\,\)　∽　\(\,\mathrm{△ACD}\,\)

利用するかどうかは問題によりますが、相似を見つけたら書き出しておく方が良いですよ。
高校入試でもそうですが、大学入試でも相似は大いに利用します。

(3)
次に、美咲さんは、
　\(\,\mathrm{△ABE}\,\)　∽　\(\,\mathrm{△ACD}\,\)
を聞いて、
　\(\,\mathrm{D,E}\,\)が\(\,\mathrm{AB,AC}\,\)の延長線上にある場合
を考え、
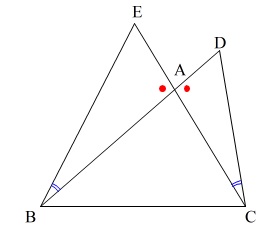\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ACD}\,\)が相似になることを証明します。

　［証明］
　\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ACD}\,\)において
　仮定から、\(\,\mathrm{∠ABE=∠ACD　･･･①}\,\)
　\(\color{black}{\fbox{\(\,\color{red}{　対頂角　}\,\)}}\)は等しいことから、\(\,\mathrm{∠BAE=∠CAD　･･･②}\,\)
①,②より、\(\color{black}{\fbox{\(\,\color{red}{　2組の角がそれぞれ等しい　}\,\)}}\)から、
　\(\,\mathrm{△ABE}\,\)　∽　\(\,\mathrm{△ACD}\,\)

ここまでは合同条件や相似条件さえ覚えておけば簡単にうめることができます。

　\(\,\mathrm{△ABE}\,\)　∽　\(\,\mathrm{△ACD}\,\)

は(4)への誘導です。

(4)はこの条件を使って解くということです。

円周角の定理の逆と面積比

(4)(3)と同じ位置に\(\,\mathrm{D,E}\,\)があるときで、
さらに条件が加わったときの\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ABC}\,\)の面積比を求めます。

　\(\color{blue}{\fbox{　条件　}}\)
　\(\,\mathrm{ＢＣ=6}\,\)
　\(\,\mathrm{ＣＤ=5}\,\)
　\(\,\mathrm{ＤＥ=2}\,\)
　\(\,\mathrm{ＥＢ=4}\,\)
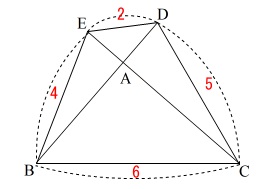面積比を求めるので単位は必要ありませんので省略してあります。
これに
　\(\,\mathrm{△ABE}\,\)　∽　\(\,\mathrm{△ACD}\,\)
の条件を利用しますが、\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ABC}\,\)の面積比を求めるだけなので
　
　\(\,\mathrm{AE}\,\)と\(\,\mathrm{AC}\,\)の比

が分ければ面積は出ます。
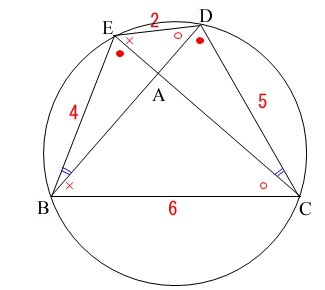(3)をはじめる目に気がついておくことですが、
\(\,4\,\)点\(\,\mathrm{B,C,D,E}\,\)は同一の円周上にあります。
（『円周角の定理の逆』）

いろいろなことがいえますが、必要な部分だけを利用します。
同じ弧の円周角は等しいので
　\(\,\mathrm{∠ADE=∠ACE}\,\)
　\(\,\mathrm{∠CBD=∠CED}\,\)
対頂角もあるのでどちらか一方でいいのですが、
　\(\,\mathrm{△ADE}\,\)　∽　\(\,\mathrm{△ACB}\,\)

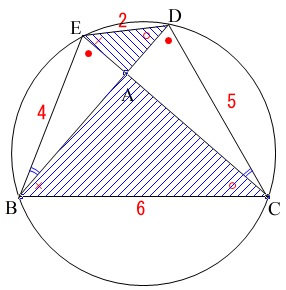
これから対応する辺の比は等しいので

\(\,\mathrm{DE:CB=2:6}\,\)なので

　\(\,\mathrm{DE:CB=1:3}\,\)　が相似比

　\(\,\mathrm{\color{blue}{AD:AC}=DE:CB=\color{blue}{EA:BA=1:3}}\,\)

また
　\(\,\mathrm{△ABE}\,\)　∽　\(\,\mathrm{△ACD}\,\)
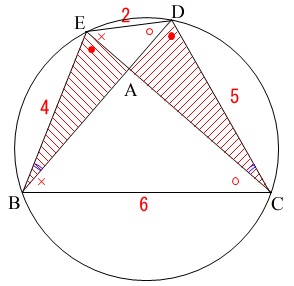相似比は
　\(\,\mathrm{EB:DC=4:5}\,\)

なので

　\(\,\mathrm{EB:DC=EA:DA=\color{red}{AB:AC=4:5}}\,\)

文字を1つだけ使いましょう。

　\(\,\mathrm{AB:AC}=4x:5x\,\)

とおきます。

　\(\,\mathrm{EA:BA=1:3}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{EA}:4x&=&1:3\\
3\mathrm{EA}&=&4x\\
\mathrm{EA}&=&\frac{4x}{3}
\end{eqnarray}\)

よって
　\(\begin{eqnarray}\displaystyle
\mathrm{EA:AC}&=&\frac{4x}{3}:5x\\
&=&4x:15x\\
&=&\color{red}{4:15}
\end{eqnarray}\)　
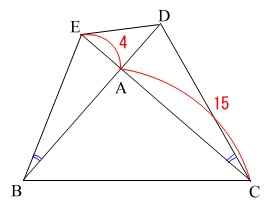\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ABC}\,\)は底辺を\(\,\mathrm{AE,AC}\,\)として高さを共通にしているので

　\(\,\mathrm{△ABE:△ABC}=\color{black}{\fbox{\(\,\color{red}{　4:15　}\,\)}}\,\)

相似を利用する順番を変えると文字を2つ使って解くこともできます。
　
　\(\,\mathrm{△ADE}\,\)　∽　\(\,\mathrm{△ACB}\,\)
なので
　\(\,\mathrm{\color{blue}{AD:AC}=DE:CB=\color{blue}{EA:BA=1:3}}\,\)
から
　\(\,\mathrm{AD:\color{red}{AC}}=x:\color{blue}{3x}\,\)
　\(\,\mathrm{EA:\color{red}{BA}}=y:\color{blue}{3y}\,\)
とおいて、
　\(\,\mathrm{△ABE}\,\)　∽　\(\,\mathrm{△ACD}\,\)
なので
　\(\,\mathrm{EB:DC=EA:DA=\color{red}{AB:AC=4:5}}\,\)
から
　\(\,\mathrm{AB:AC}=\color{red}{4:5}=\color{blue}{3y:3x}\,\)
としても同じ結果がでますが文字を1つで処理できる順序で進めました。

大した差はないのでどちらでもいいですよ。
数学の解法は1つではありません。

　\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ABC}\,\)の面積比を底辺の比
としたところは
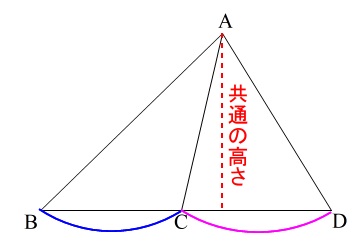2つの三角形の高さが共通
なので、
　\(\,\mathrm{△ABC:△ACD:△ABD=\color{blue}{BC}:\color{red}{CD}：BD}\,\)
となるのと同じで、

　\(\begin{eqnarray}
\mathrm{△ABE:△ABC}&=&\mathrm{AE:AC}\\
&=&\color{black}{\fbox{\(\,\color{red}{　4:15　}\,\)}}
\end{eqnarray}\)　