秋田県で2018年(平成30年度)に行われた公立高校入試の数学の過去問（第2問）の解説です。
ここでは一般選抜試験の問2の解説になります。
問1と同じように2次関数の基本性質と文字式の証明や作図および標本調査の小問集合です。
問題は秋田県の公式サイトにもあります。
\(\,\large{2}\,\)
(1)
①放物線の増減を見る問題です。
イメージで進められれば素晴らしいですが、ちょっとした思い込みでミスしますので関数の問題ではグラフを書いて考ることを忘れないようにしましょう。
『関数\(\,y=-x^2\,\)の増減について』と問題にあれば図で確認すれば良いのですが、この小問集合では図がありません。
普通なら関数問題ではグラフを書いてくれていますが、ここでは『グラフを書いて』という問題作成者の思いがあるのではないでしょうか。
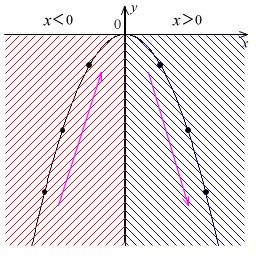関数\(\,y=-x^2\,\)は上に凸な（下に開いた）グラフになります。
『\(\,x\,\)が増加するとき』、というのは\(\,x\,\)が左から右に移動するということです。
\(\,x＜0\,\)の範囲（赤部分のグラフ）では増加
\(\,x＞0\,\)の範囲（青部分のグラフ）では減少
していますので、（答え） \(\,\underline{ \color{red}{ウ} }\,\)
②変化の割合です。
\(\,\displaystyle \color{red}{変化の割合=\frac{ y\,の増加量 }{ x\,の増加量 }}\,\)
変化の割合を示す\(\,2\,\)点の座標を書き出せば分かり易いです。
\(\,x\,\)が\(\,a\,\)から\(\,a+1\,\)までどうかするので、
\(\,x=a\,\)のときと\(\,x=a+1\,\)のときの座標を書き出します。
\(\,(\,a\,,\,-a^2\,)\,\)
\(\,(\,a+1\,,\,-(a+1)^2\,)\,\)
それぞれの座標で引き算して増加量を出しますが、座標を縦に並べると引き算しやすいです。
ただ、\(\,x\,\)座標\(\,y\,\)座標ともに同じ方向に引き算しないと変化の割合は符号が逆になるので注意しましょう。
どちらでも良いですが、下から上を引くと決めておくと良いです。
筆算は上から下を引くので上から下でもかまいません。
同じ方向にそろえていればどっちでも良いです。
このサイトでは「下から上を引く」で統一しています。
理由はありますが説明はしません。（どちらでも良いです。）
\(\hspace{10pt}\displaystyle \frac{-(a+1)^2-(-a)^2}{(a+1)-(a)}\\
\displaystyle =\frac{-(a^2+2a+1)-(-a^2)}{a+1-a}\\
\displaystyle =\frac{-a^2-2a-1+a^2}{1}\\
=-2a-1\)
この変化の割合が「\(\,5\,\)である」ときなので
\(\begin{eqnarray}
-2a-1&=&5\\
-2a&=&5+1\\
-2a&=&6\\
2a&=&-6\\
a&=&\underline{ \color{red}{-3} }
\end{eqnarray}\)
変化の割合はよく聞かれます。
1次関数の場合は傾きと等しくなるので確認しておくと良いですね。
(2)
文字式の証明です。
「幸太さん」、誰でも良いです。笑
問題は、
『3つの連続する偶数の和は\(\,6\,\)の倍数になることを証明しなさい。』
です。
\(\,n\,\)を整数とすると連続する偶数は
\(\,2n\,,\,2n+2\,,\,2n+4\,,\,2n+6\,,\cdots\,\)
このように一番小さい偶数を\(\,2n\,\)とすると\(\,2\,\)ずつ増えます。
⇒ 中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)
文字式で連続する偶数が表せたら、
問題の条件通りに計算すれば必ず\(\,6\,\)の倍数になるはずです。
解答欄をうめていきます。
［説明］
\(\,n\,\)を整数とすると、連続する3つの偶数は小さいものから順に、
\(\,2n , \color{black}{\fbox{\(\,\color{red}{ 2n+2 }\,\)}} , \color{black}{\fbox{\(\,\color{red}{ 2n+4 }\,\)}}\,\)
と表すことができる。
このとき、連続する3つの偶数の和は、
\(\hspace{10pt}2n+(2n+2)+(2n+4)\\
=2n+2n+2+2n+4\\
=6n+6\\
=6(n+1)\)
\(\,n+1\,\)は整数なので\(\,6(n+1)\,\)は\(\,6\,\)の倍数となる。
したがって、連続する3つの偶数の和は、\(\,6\,\)の倍数である。
（終わり）
\(\,6\,\)の倍数の和が\(\,6\,\)の倍数になるということは整数の性質として一般に言えるので、
因数分解せずに
\(\,6n+6\,\)
の段階で「\(\,6\,\)の倍数の和は\(\,6\,\)の倍数であるから」と書いておいても減点はないでしょう。
ただ、受験の段階では因数分解できるはずなので因数分解している方が無難です。
(3)
\(\,45°\,\)の作図です。
\(\,45°\,\)の作図方法はパッと思いつく範囲で3つあります。
・\(\,90°\,\)（直角）の角の二等分線
・中心角\(\,90°\,\)の円周角
・直角二等辺三角形の底角
他にも「正八角形の外角」もありますが、正八角形の書き方から説明しなくてはならないので省略します。
直角二等辺三角形が一番はやそうなのでしぼります。
この場合\(\,A\,\)は関係ありません。
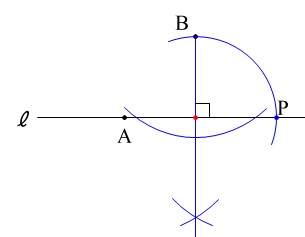
直線\(\,\ell\,\)を底辺とする直角二等辺三角形を書けば\(\,∠\mathrm{BPA}=45°\,\)になります。
\(\,\mathrm{B}\,\)から\(\,\ell\,\)に垂線を引くと、
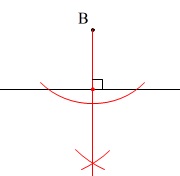この交点を\(\,\mathrm{M}\,\)とでもおくと
\(\,\mathrm{△BPM}\,\)が頂角を\(\,\mathrm{M}\,\)とする直角二等辺三角形になればいい。
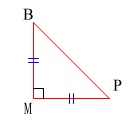なので、
交点を中心に交点と\(\,\mathrm{B}\,\)までを半径とする円
を描いて\(\,\ell\,\)との交点を\(\,\mathrm{P}\,\)とすれば終わりです。
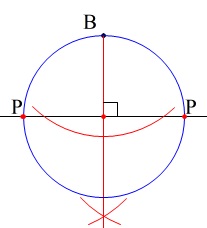
2つありますが問題に「このうち1つを」とあるのでどちらか1つを示します。
(4)
標本調査は調査する数が多いとき、
一部を調査して全体を推測することなので正確な値ではありません。
そのため答えには「およそ」をつけます。
一部の調査を数回行った場合は平均を利用します。
この問題では平均を出してくれていますのでそのまま使えます。
\(\,27:3\,\)
となっており、
緑色の豆の個数を\(\,x\,\)とすると黒色の豆\(\,100\,\)個との比も同じで
\(\,27:3=x:100\,\)
とおくことができる。
この比例式を解くと、
\(\begin{eqnarray}
27:3&=&x:100\\
3x&=&27\times 100\\
x&=&900
\end{eqnarray}\)
よって、およそ\(\,\underline{ 900 個 }\,\)
「考え方が分かるように過程も書くきなさい。」
と問題に書いてあるので上のように書いておけば大丈夫でしょう。
\(\,\large{2}\,\) だけで\(\,23\,\)点です。
⇒ 2018(H30)年度秋田県公立高校入試数学の過去問第3問の解説
問3は平面図形総合問題です。
⇒ 秋田県公立高校入試2018数学の過去問と解説
\(\,\large{1}\,\) と \(\,\large{2}\,\) を合わせて\(\,50\,\)点以上あるので、いったん見直ししても良いですね。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
