空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

空間図形の問題で平行な線分、ねじれの位置にある辺、辺と垂直な面、面と平行な面など位置関係を聞いてくることがよくあります。
特に、交わりとねじれの位置をかん違いしている人も多いので注意しておくと良いですよ。
これらの位置関係の問題を例題を取り上げて説明しておきます。

空間図形の位置関係

空間図形は中学１年の図形として最後の単元ですが、
今後空間図形を特別に取り上げることはありません。

合同や相似といった平面上の性質は中学の間に追加して出てきます。
もっと詳しい平面幾何も高校で学習します。

しかし、空間図形はこの単元で終わりです。

大学入試でも苦手にしている人は多い空間問題ですが、
　空間は面の組み合わせでできている
ということをここで理解していないと後々苦手なままですよ。

ちょっとしたことで難しい問題も難しくなくなる方法もあるので、
あまり苦手意識を持たず取り組んで行って下さい。

ここでは空間図形でも新しい用語が出てきますので、
ひらがなを覚えるつもりで意味を覚えておきましょう。

位置関係がいろいろとありますので、
まとめて問題を先に書いておきます。

すぐに答えが分かるようなら用語の意味は理解できていると考えて良いでしょう。

問題１－１

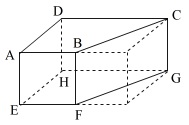
右の図は直方体を1つの平面で切ってできた立体で、
\(\,\mathrm{AE\,//\,BF}\,\)です。
(1) 辺\(\,\mathrm{DC}\,\)と平行な辺はいくつあるか答えなさい。
(2) 辺\(\,\mathrm{DC}\,\)とねじれの位置にある辺をすべて答えなさい。
(3) 辺\(\,\mathrm{EF}\,\)と垂直な面を答えなさい。
(4) 面\(\,\mathrm{AEHD}\,\)と平行な面はあるか答えなさい。

平行な辺と辺

(1)
平行という言葉は、辺どうしでも使いますし、面どうしでも使います。

面と面が平行な場合や、
辺と面が平行というのは、
　どこまで行っても交わらないことが条件
なので分かり易いですが、
辺と辺が平行というときは条件が加わってきます。

「ある辺に平行な辺」とは、
　どこまで行っても交わらず、
　同じ方向（あるいは反対）をむいている辺
のことです。
赤線が辺\(\,\mathrm{DC}\,\)に平行な線分です。

「交わらない」だけでは、
「ねじれ」もそうなので図で感覚的に覚えた方が早いですね。

答えは、\(\,\underline{　３つ　}\,\)。

『平行の線分を答えなさい。』
という問題なら答えは違ってきますよ。

　「\(\,\mathrm{辺AB\,,\,辺EF\,,\,辺HG}\,\)」
と具体的に答えなければなりませんので、
この問題に限らず問題が何を聞いているかはよく読んでおきましょう。

ところで、
これが「面\(\,\mathrm{ABCD}\,\)に平行な辺」となるとちょっと違ってきます。

「面に平行な辺」は、
どこまで行ってもその面と交わらない辺のことなので、
平行な面の中にある辺は
すべてもう一方の面に平行なので、
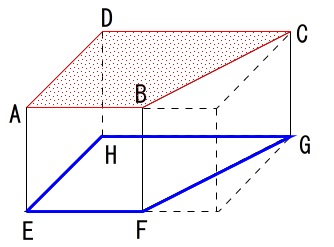青線はすべて赤い面に平行な辺になります。

　\(\,\mathrm{EF,FG,GH,HE}\,\)
は線分も直線も面\(\,\mathrm{ABCD}\,\)に平行です。
（面自体が平行なのですべての辺やそれを延長した直線は平行になります。）

辺に平行なのか、面に平行なのか、良く問題を読みましょう。

辺とねじれの位置にある辺

ねじれの位置はよく聞かれるので注意しておくと良いです。

(2)『辺\(\,\mathrm{DC}\,\)とねじれの位置にある辺をすべて答えなさい。』

「ねじれの位置」とは、
　平行でもなく、
　交わりもしない、
辺(直線)のことです。

直線と書いたのは、
延長して交わる辺は「ねじれの位置」とは言わないからです。
これはちょっとひねった問題でよく聞かれることなので覚えておきましょう。

例えば、辺\(\,\mathrm{AD}\,\)と辺\(\,\mathrm{BC}\,\)は平行ではありません。
交わりもしていませんが、\(\,\mathrm{BC}\,\)を延長すると、
同じ平面上にあるのでいずれ交わります。

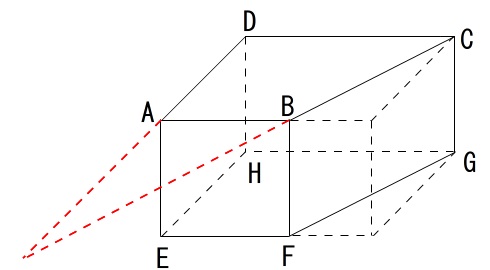
こういう位置関係は「ねじれとは言わない」のです。

ここではそこまで考えなくて良いので、
「ねじれの位置」にある辺は、

答え　\(\,\mathrm{\underline{　辺AE\,,\,辺BF\,,\,辺EH\,,\,辺FG　}}\,\)

の4つです。

辺と垂直な面

(3) 『辺\(\,\mathrm{EF}\,\)と垂直な面を答えなさい。』
「垂直な面」は簡単です。

垂直に串刺しにされている面のことです。

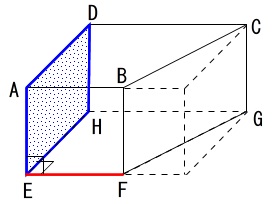
面\(\,\mathrm{\color{blue}{AEHD}}\,\)しかありません。

面\(\,\mathrm{BCGF}\,\)は垂直ではありませんよ。

ここで知っておかないと大きな差となる垂直関係を1つお伝えしておきます。

1つの平面に垂直な直線（線分）は、
平面上のどの直線とも垂直です。

わかりにくいかもしれないので説明しておきます。
例えば、1つの直方体をみてみましょう。
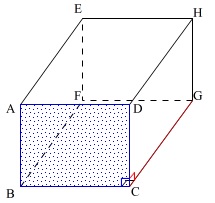線分\(\,\mathrm{GC}\,\)と面\(\,\mathrm{ABCD}\,\)は垂直です。

このとき、
\(\,\mathrm{GC}\,\)は\(\,\mathrm{BC}\,\)や\(\,\mathrm{DC}\,\)とも垂直ですが、
\(\,\mathrm{AC\,,\,AD\,,\,AB}\,\)とも垂直です。

平らな台に垂直に棒を立てたところをイメージしてみると、
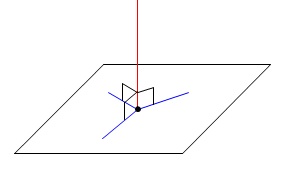台上の直線はすべて、
垂直に立っている棒と垂直になっているのが分かりますよね？

イミージが取れない場合は机に鉛筆を立てて、
机の上の直線と立てた鉛筆が垂直なのを確認してみて下さい。

特に\(\,\mathrm{AC}\,\)と\(\,\mathrm{GC}\,\)が垂直であることは
良く利用しますのでイメージできるようにしておいた方が良いですよ。

それと、
　『\(\,\mathrm{AD}\,\)と\(\,\mathrm{GC}\,\)は交わってないじゃないか、』
と思うかもしれませんが、
ねじれの位置にある2つの直線の角度は、
（簡単にいうと）
　平行移動して重ねたときの角度
をいいますので覚えておくと良いです。

面と平行な面

(4) 面\(\,\mathrm{AEHD}\,\)と平行な面はあるか答えなさい。
平行な面とは、
どこまで広げても交わる部分がない面どうしのことです。
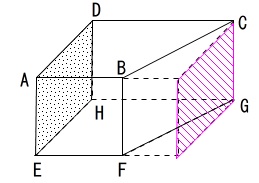面\(\,\mathrm{AEHD}\,\)に平行な面は、
切り取る前の直方体の対面ですがカットされているので、
平行な面は、\(\,\underline{　ない　}\,\)、が答えです。