2019年度神奈川県公立高校入試の数学問7平面図形問題の解説

2019年度神奈川県で行われた公立高校入試の数学問題問7の解説です。
問7は平面図形ですが問3とは違い証明があります。
円周角の定理から入りますが、条件付きの穴埋めがあり、三平方の定理、相似比の利用と総合的な問題です。

問題は神奈川県の公式サイトにもあります。

⇒　2019年度神奈川県立高校入試数学問題

問\(\,7\,\)

円周上に\(\,3\,\)点\(\,\mathrm{A,B,C}\,\)と\(\,\mathrm{P}\,\)がある図\(\,1\,\)の条件があります。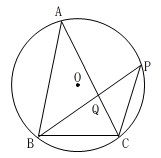

　\(\,\mathrm{AC\,＞\,AB\,＞\,BC}\,\)
　\(\,\mathrm{B}\,\)と反対側の\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AC}}}\,\)上に\(\,\mathrm{P}\,\)
　\(\,\mathrm{AC}\,\)と\(\,\mathrm{BP}\,\)の交点を\(\,\mathrm{Q}\,\)

一番最初の
　\(\,\mathrm{AC\,＞\,AB\,＞\,BC}\,\)
は難しく考えなくて良いです。
点\(\,\mathrm{A}\,\)が中心の真上よりちょっと左に寄っている、くらいに考えておけば条件を満たします。

ただし、（イ）では余計な場合を省くために必要な条件です。

（ア）
相似の証明です。
図形の証明は図の中で完成させてから書き出すのが基本ですが、この問題は利用を選択するだけなので問題の書いてある順番に理由を探せば良いですよ。

　\(\,\mathrm{△ABQ}\,\)　∽　\(\,\mathrm{△PCQ}\,\)

を証明しますが、図に条件から分かることを書いていけば自然に答えは見つかります。

　弧、または弦\(\,\mathrm{BC}\,\)に対する円周角は等しい
　弧\(\,\mathrm{AP}\,\)に対する円周角は等しい
　対頂角は等しい

などを図示すると証明は終わっています。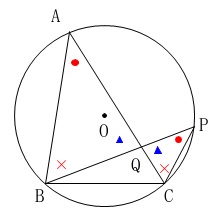\(\,\mathrm{AP}\,\)を結べば他にも出てきますがこれだけあれば証明には十分でしょう。

図の中で証明できていないのに、証明を文章で書くなんてことはできませんよ、

［証明］の文章に合わせて答えを選んでいきましょう。

　『（ⅰ）から』と理由を聞いているので
（ⅰ）は\(\,\mathrm{∠BAC=∠BPC}\,\)となる理由です。

　\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{BC}}}\,\) に対する円周角

ですね。

　\(\,\underline{　\mathrm{\stackrel{\large{\frown}}{\mbox{BC}}}\, に対する円周角は等しい　}\)

次に、\(\,\mathrm{∠AQB=∠PQC}\,\)となる理由です。

　\(\,\underline{　対頂角は等しい　}\,\)

この、2組の角がそれぞれ等しいという相似条件から

　\(\,\mathrm{△ABQ}\,\)　∽　\(\,\mathrm{△PCQ}\,\)

が証明されました。

相似の証明は、相似条件となる3つのうちどれかをいえば良いのです。

相似条件を知らなければ証明はできませんが、
　合同条件5つ
　相似条件3つ
を覚えていない人はいないと思うので、大丈夫ですね。

（イ）
今度は点\(\,\mathrm{P}\,\)が移動しますが、条件を満たしたとき\(\,\mathrm{P}\,\)は固定されるので動点問題ではありません。

この問題ではただし書きがあります。
　
　『ただし、「AB」を必ず用いること。』

これが何を意味しているのかは後で分かります。

まずは基本通り条件を書き出し、図に書き込んで行きましょう。

　\(\color{red}{\fbox{　条件　}}\)

　\(\,\mathrm{△ABQ}\,\)と\(\,\mathrm{△PCQ}\,\)は常に相似

これは（ⅰ）で証明しました。
\(\,\mathrm{P}\,\)の位置に関係なく成り立っています。

　\(\,\mathrm{AB=CP}\,のとき\,\mathrm{△ABQ≡△PCQ}\,\)

このことは問題が示してくれているので証明しなくて良いです。
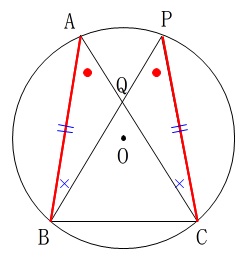\(\,1\,\)辺とその両端の角がそれぞれひとりので合同が言えています。

同じ、または同じ長さの弧に対する円周角が等しいことを利用しますが（ⅰ）で図に書いているので証明の必要がありません。
相似の証明を問題にしているので合同の証明は問題にしなかったということでしょう。

というより
　\(\,\mathrm{△ABQ}\,\)と\(\,\mathrm{△PCQ}\,\)は常に相似
ですね。

『また、\(\,\mathrm{△ABQ}\,\)と\(\,\mathrm{△PCQ}\,\)が二等辺三角形になるのは』

ですが、\(\,\mathrm{△ABQ}\,\)が二等辺三角形になるのは、

　\(\mathrm{\color{blue}{AB=AQ}\,,\,\color{blue}{AQ=BQ}\,,\,\color{red}{AB=AC}}\)

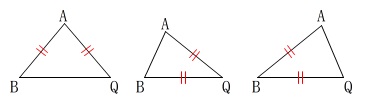
の場合があります。

二等辺三角形になるのは\(\,\mathrm{AB=AQ}\,\)や

　\(\,\mathrm{\color{blue}{AQ=BQ}}\,\)のとき

と書きたいところですがただし書きがあるのです。

　『ただし、「AB」を必ず用いること。』

　\(\,\mathrm{\color{red}{AB=AC}}\,\)

は問題の最初の条件\(\,\mathrm{AC\,＞\,AB\,＞\,BC}\,\)を満たしていないので考えなくて良いです。

　\(\mathrm{\color{blue}{AB=AQ}}\)の場合、
\(\,\mathrm{A}\,\)がもう少し左下にある場合も考えれば二通り考えられます。
相似と合同ですが、合同になる方は図の\(\,\mathrm{A}\,\)が固定と見て、考えなくて良いでしょう。
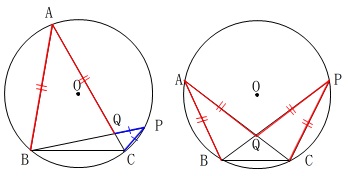この場合について問題では二等辺三角形になるといってくれているのであまり考えなくて良いです。

もう一つ、\(\,\mathrm{\color{blue}{AQ=BQ}}\,\)の場合です。
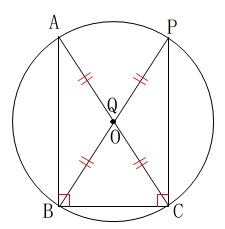この場合\(\,\mathrm{AC}\,\)と\(\,\mathrm{BP}\,\)は直径になるので、
　\(\,\mathrm{∠ABC=∠BCP=90^{\circ}}\,\)

このことから
　\(\,\underline{　\mathrm{AB\,/\!/\,PC}　}\,\)
のとき二等辺三角形になります。

二等辺三角形の底角が等しくなることから錯角が等しいと見ても結果は同じです。

（ウ）
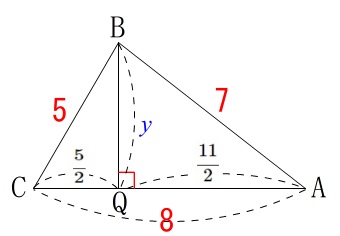
図\(\,2\,\)の条件を書き出します。

　\(\,\mathrm{AC⊥BP}\,\)
　\(\,\mathrm{AB=7}\,\)
　\(\,\mathrm{AC=8}\,\)
　\(\,\mathrm{BC=5}\,\)
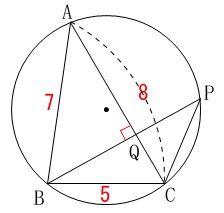このとき\(\,\mathrm{BP}\,\)の長さを求めます。

条件は1つも見逃してはいけません。

　　\(\,\mathrm{AC⊥BP}\,\)

なので三平方の定理の基本的な使い方ですね。

さっさと求めても良いのですが\(\,\mathrm{△ABC}\,\)を抜き出して説明します。
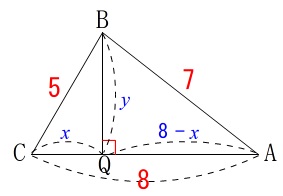ここではていねいに\(\,\mathrm{CQ}=x\,,\,\mathrm{BQ}=y\,\)とおきますが、
\(\,\mathrm{CQ}=x\,\)おくだけですべての長さは求まります。

\(\,\mathrm{△BCQ}\,\)に三平方の定理を用いると

　\(\begin{eqnarray}
\mathrm{CQ^2+BQ^2}&=&\mathrm{BC^2}\\
x^2+y^2&=&5^2　･･･①
\end{eqnarray}\)

\(\,\mathrm{△ABQ}\,\)に三平方の定理を用いると

　\(\begin{eqnarray}
\mathrm{AQ^2+BQ^2}&=&\mathrm{AB^2}\\
(8-x)^2+y^2&=&7^2　･･･②
\end{eqnarray}\)

①②から\(\,y^2\,\)を消去します。

①から
　\(\,y^2=5^2-x^2　･･･\color{red}{①’}\,\)
②から
　\(\,y^2=7^2-(8-x)^2　･･･②’\,\)

連立することになりますが左辺は同じなので右辺どうしが等しくなります。

　\(\begin{eqnarray}\displaystyle
7^2-(8-x)^2&=&5^2-x^2\\
49-(64-16x+x^2)&=&25-x^2\\
49-64+16x\color{red}{-x^2}&=&25\color{red}{-x^2}\\
-15+16x&=&25\\
16x&=&40\\
x&=&\frac{40}{16}=\frac{5}{2}
\end{eqnarray}\)

このことから
　\(\displaystyle \mathrm{CQ=\frac{5}{2}}\,\)
　\(\displaystyle \mathrm{AQ}=8-\frac{5}{2}=\frac{11}{2}\)
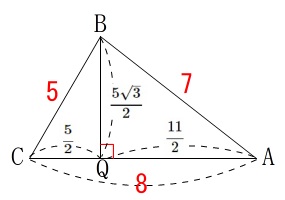
再び\(\,\mathrm{△CBQ}\,\)に三平方の定理を用いて、ですが\(\,\color{red}{①’}\,\)に戻せば良いだけです。

　\(\begin{eqnarray}\displaystyle
y^2&=&5^2-x^2\\
&=&5^2–\left(\frac{5}{2}\right)^2\\
&=&25-\frac{25}{4}\\
&=&\frac{75}{4}\\
y&=&\pm \frac{5\sqrt{3}}{2}
\end{eqnarray}\)

\(\,y\,\)は長さなので\(\,y\,＞\,0\,\)だから
　\(\displaystyle y=\mathrm{BQ}=\frac{5\sqrt{3}}{2}\,\)
やっと最初の相似を使います。

　\(\,\mathrm{△ABQ}\,\)　∽　\(\,\mathrm{△PCQ}\,\)
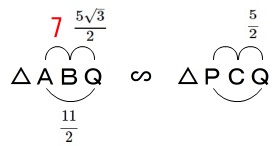欲しいのは\(\,\mathrm{PQ}\,\)の長さなので\(\,\mathrm{PQ}\,\)を含む比例式を立てます。

　\(\begin{eqnarray}\displaystyle
\mathrm{AQ:\color{red}{PQ}}&=&\mathrm{BQ:CQ}\\
\frac{11}{2}:\mathrm{\color{red}{PQ}}&=&\frac{5\sqrt{3}}{2}:\frac{5}{2}\\
\frac{5\sqrt{3}}{2}\,\mathrm{\color{red}{PQ}}&=&\frac{11}{2}\times \frac{5}{2}\\
10\sqrt{3}\,\mathrm{\color{red}{PQ}}&=&11\times 5\\
\mathrm{\color{red}{PQ}}&=&\frac{11\times 5}{10\sqrt{3}}\\
&=&\frac{11}{2\sqrt{3}}\\
&=&\frac{11\sqrt{3}}{6}
\end{eqnarray}\)
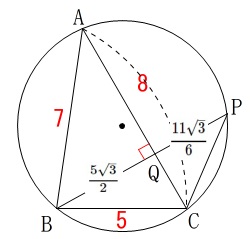求める長さは\(\,\mathrm{BP}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{BP}&=&\mathrm{BQ+PQ}\\
&=&\frac{5\sqrt{3}}{2}+\frac{11\sqrt{3}}{6}\\
&=&\frac{15\sqrt{3}+11\sqrt{3}}{6}\\
&=&\frac{26\sqrt{3}}{6}\\
&=&\underline{　\frac{13\sqrt{3}}{3}　}
\end{eqnarray}\)

以上です。

⇒　神奈川県公立高校入試問題(平成30年度)の数学の過去問解説(公開)

昨年と傾向は同じです。
教科書の全範囲から偏りなく、基本中心に、応用を含めた出題形式で、中学数学の良い復習になります。

⇒　中学数学のすべてを短期で習得する『覚え太郎』

高校受験の数学の問題はすべてこの中から作られています。