平成30年度に神奈川県で実施された公立高校入試の数学問題の解説です。
神奈川県の2018過去問ですが公立高校は出題内容が教科書からなのでどこも同じです。
解答の添付だけではなく過去問解説なのでちょっと長いですが、見て少しでも参考にして下さい。
神奈川県の公立入試問題は県の公式サイトにもあります。
基本的にすべきことはすでに伝わっている(『覚え太郎』は見ている)会員向けに解いていますので、聞いたことが無いことがあるかもしれませんが難しいことはいっていませんので、「そうなんだ」と納得して進めて下さい。
\(\,2019\,\)年度の問\(\,1\,\)問\(\,2\,\)の解説は
⇒ 2019年度神奈川県公立高校入試の数学問題問1,2の解説
問1 計算問題の小問集合
神奈川県の特徴で答えを番号で選ぶようになっていますが、答えの欄に数値や式を書かないというだけで、普通の試験と同じように自分でしっかり計算はするようにしましょう。
(ア)
\((-8)+(-4)\\
=-8-4\\
=-12\)
かっこを外した式を書くことで計算ミスを減らせるという説明は必要無いですよね。
(イ)
\(\displaystyle -\frac{5}{7}+\frac{2}{3}\\
\displaystyle =\frac{-5\times \color{red}{3}+2\times \color{red}{7}}{\color{red}{21}}\\
\displaystyle =\frac{-15+14}{21}\\
\displaystyle =\frac{-1}{21}=-\frac{1}{21}\)
もちろん通分しますが分母は一つにして、分子の計算に集中します。
分数のマイナス(-)符号は、分数の前か、分子におきます。
途中計算では分母に置いておいても良いですが、答えにはおきません。
(ウ)
\(65a^2b \div 5a\\
\displaystyle =\frac{\color{red}{65}a^2b}{\color{red}{5}a}\\
\displaystyle =\frac{13\color{red}{a^2}b}{\color{red}{a}}\\
=13ab\)
何個あっても割り算の後ろ(直後だけ)は分母に回すんですよ。
2行目から3行目は必要ありませんが、係数、\(a\) の項、\(b\) の項、の順で書いていけば良いので書いておきました。
たいして時間は変わらないでしょう?
(エ)
\(\displaystyle \frac{18}{\sqrt{2}}-\sqrt{98}\\
=\displaystyle \frac{18\times \color{red}{\sqrt{2}}}{\sqrt{2}\times \color{red}{\sqrt{2}}}-7\sqrt{2}\\
=\displaystyle \frac{\color{red}{18}\sqrt{2}}{\color{red}{2}}-7\sqrt{2}\\
=9\sqrt{2}-7\sqrt{2}\\
=2\sqrt{2}\)
無理数の有理化と引き算ですが、ていねいにやりましょう。
\(\sqrt{98}=\sqrt{2\times 7 \times 7}=\sqrt{2\times 7^2}=7\sqrt{2}\)
はルートの中を素因数分解すれば出てきます。
問題用紙のすき間で必ず確認するようにしましょう。
(オ)
\((x+9)^2-(x-3)(x-7)\\ \\
=(x^2+18x+81)\color{red}{-}(x^2-10x+21)\\ \\
=x^2+18x+81-x^2\color{red}{+}10x\color{red}{-}21\\ \\
=28x+60\)
計算ミスを減らす1行はどこかわかりますよね?
こういうところで焦ってミスすると大きいですよ。
簡単な計算ですが、暗算はしないことです。
暗算して結果が出ればかっこいいように見えるかもしれないけど、この程度暗算しても大してかっこよくないです。笑
答えをきっちり出した方が断然かっこいい。
(会員は十分わかっていると思うけど。)
問2 小問集合第二弾
(ア)
\((x+4)^2-2(x+4)-24\)
まとまっているので \((x+4)=A\) とおくと
\((x+4)^2-2(x+4)-24\\ \\
=A^2-2A-24\)
ここで定数項の符号なしの数値\(\color{magenta}{\fbox{24}}\)は
\(\color{black}{\fbox{1×24}}\) \(\color{black}{\fbox{2×12}}\) \(\color{black}{\fbox{3×8}}\) \(\color{red}{\fbox{4×6}}\)
のどれかの組で1次の係数を\(\color{red}{\fbox{-2}}\)にできるのは
\(\color{red}{\fbox{4×6}}\) だけです。
\((x+4)^2-2(x+4)-24\\ \\
=A^2-2A-24\\ \\
=(A\color{red}{+4})(A\color{red}{-6})\)
\(A=x+4\) を戻して、
\((A+4)(A-6)\\ \\
=(x+4+4)(x+4-6)\\ \\
=\underline{(x+8)(x-2)}\)
もちろん最初の段階で展開しても同じ結果です。
\((x+4)^2-2(x+4)-24\\ \\
=(x^2+8x+16)-2(x+4)-24\\ \\
=x^2+8x+16-2x-8-24\\ \\
=x^2+6x-16\\ \\
=\underline{(x+8)(x-2)}\)
どちらでも大して変わりませんので思いついた方で突っ走って、
見直しの段階で違う方法で確認すれば良いですよ。
(イ)
\(6x^2-2x-1=0\) を解くことになりますが、
\(x^2\) の係数が1でないとき全体が同じ数で割れないときは解の公式です。
2次方程式 \(ax^2+bx+c=0\) の解の公式は
\(\displaystyle \color{red}{\large{x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}}}\)
これに、 \(6x^2-2x-1=0\) の係数を当てはめて計算するだけです。
\(a=6\,,\,b=-2\,,\,c=-1\) なので
\(\displaystyle x=\frac{-(-2)\pm \sqrt{(-2)^2-4\times (6)\times (-1)}}{2\times 6}\\
\displaystyle =\frac{2\pm \sqrt{4+24}}{12}\\
\displaystyle =\frac{2\pm \sqrt{28}}{12}\\
\displaystyle =\frac{2\pm 2\sqrt{7}}{12}\\
\displaystyle =\frac{1\pm \sqrt{7}}{6}\)
最後の約分はすべての項が2で割れるから約分できるんですよ。
解の公式は覚えておきましょう。
導いてもしれていますが、時間の無駄です。
覚え方は知っていますよね。だいたい3日あれば口が覚えます。笑
(ウ)
\(\displaystyle \color{magenta}{(\,変化の割合\,)}=\frac{\color{blue}{(\,y\,の増分) \hspace{5pt}}}{\color{red}{(\,xの増分\,) \hspace{5pt}}} ・・・①\)
です。
\(y=ax^2\) なので
\(x=2\) のとき、\(y=a\times (2)^2=4a\)
\(x=5\) のとき、\(y=a\times (5)^2=25a\)
これから
\((x の増分)=5-2=\color{red}{3}\)
\((y の増分)=25a-4a=\color{blue}{21a}\)
\((変化の割合)=\color{magenta}{-4}\)
を①に入れれば良いだけです。
\(\begin{eqnarray}
\displaystyle \color{magenta}{-4}&=&\frac{\color{blue}{21a}}{\color{red}{3}}\\
-12&=&21a\\
21a&=&-12\\
\displaystyle a&=&\frac{-12}{21}=\underline{-\frac{4}{7}}
\end{eqnarray}\)
文字を含むと難しく感じますが、変化の割合の関係式は変わるわけではありません。
1行目から2行目は
\(\displaystyle -4=\frac{\color{red}{21}a}{\color{red}{3}}\,\Rightarrow\,-4=7a\)
としても良いですが、いつでも約分できるとは限らないのでいつも通り処理しておきました。
(エ)
例えば50円鉛筆を9本買ったら
\(50\times 9=450円\)
と計算しますよね。
実際に買い物をするときの計算通り文字を当てはめていけば良いのですよ。
1本 \(a\) 円の鉛筆9本の代金は \(9\times a\) 円
消しゴム1個 \(100\) 円 と合わせると
\(9a+100\)
が支払う代金合計です。
おつりがあったということは支払いに使った1000円の方が多かったからです。
足りなかったらおつりをくれるどころか、足りないよ、とさいそくされます。
だから大小関係は
\(\underline{9a+100<1000\hspace{5pt}}\)
代金の問題は実際の買い物をイメージして関係式を出せば良いです。
買い物したことないなら自分で買い物して下さい。
(オ)
ルートのついた数が整数(自然数)になる、ということはルートの中身が平方数ですね。
\(53-2n=○^2\)
\(n\) は正の整数(自然数)と限定してくれているので、○に整数が入り数字を調べ尽くせば良いだけです。
例えば
\(53-2n=0^2\) になる \(n\) はあるか?
\(53-2n=1^2\) になる \(n\) はあるか?
です。
それくらいの解く気持ちは持っておきましょう。
調べていくうちに気がつくことも多いですよ。
といっても53より小さい平方数は、
\(0^2\,,\,1^2\,,\,2^2\,,\,3^2\,,\,4^2\,,\,5^2\,,\,6^2\,,\,7^2\)
しかありません。
(\(8^2=64\) で \(n\) が負の数でなければ出ない数字)
なので○には8より小さい数しか入ることはありません。
ただ、\(53-2n\) は奇数から偶数を引いているので奇数です。
だから \(53-2n\) が平方数になるのは
\(\,1^2\,,\,3^2\,,\,5^2\,,7^2\)
の \(\underline{4個}\) だけです。
この問題は \(n\) を具体的には聞いていませんので、出す必要はありませんが
\(53-2n=1^2\) から \(n=26\)
このとき
\(\sqrt{53-2\times 26}=\sqrt{1}=\color{red}{1}\)
\(53-2n=3^2\) から \(n=22\)
このとき
\(\sqrt{53-2\times 22}=\sqrt{9}=\color{red}{3}\)
\(53-2n=5^2\) から \(n=14\)
このとき
\(\sqrt{53-2\times 14}=\sqrt{25}=\color{red}{5}\)
\(53-2n=7^2\) から \(n=2\)
このとき
\(\sqrt{53-2\times 2}=\sqrt{49}=\color{red}{7}\)
と確かに整数になっていますね。
この問題は慣れるまでは○の数を1から増やして調べる方がはやいです。
○が8にたどり着いたら \(n\) は正の整数ではなくなる、ということに気がつきます。
(慣れてからでも私なら調べ尽くします。笑)
(カ)
度数分布表の読み取りです。
覚え太郎や基礎レポートで詳しく説明しているし、
すでに長くなりつつあるので、当たり前に知っているものとします。
度数分布表では一つの階級に属する人はすべて、階級値であると見なします。
階級値とは階級の真ん中の数値です。
だから
\(10\,\mathrm{m}~14\,\mathrm{m}の階級にいる人1人は12\,\mathrm{m}\)
\(14\,\mathrm{m}~18\,\mathrm{m}の階級にいる人3人は16\,\mathrm{m}\)
\(18\,\mathrm{m}~22\,\mathrm{m}の階級にいる人8人は20\,\mathrm{m}\)
\(22\,\mathrm{m}~26\,\mathrm{m}の階級にいる人6人は24\,\mathrm{m}\)
\(26\,\mathrm{m}~30\,\mathrm{m}の階級にいる人2人は28\,\mathrm{m}\)
投げたということになります。
\(\displaystyle 平均値=\frac{総得点}{人数合計}\)
なので、
\(\displaystyle \frac{12\times 1+16\times 3+20\times 8+24\times 6+28\times 2 }{20}\\ \\
\displaystyle =\frac{12+48+160+144+56}{20}\\ \\
\displaystyle =\frac{420}{20}=\underline{21.0}\)
多くの場合あるのですがこの問題では小数第何位を四捨五入などという指定はありません。
この問題は選択なので「21.0」を選べばいいのです。
指定がなければ記述の場合は、「21」でしょうね。
度数分布表しかない場合、有効数字はないものとして考えないと、有効数字は一体どこまで測ったの?
と永久に悩まなければなりません。
問3 図形と文章題の小問集合
(ア)
図形の位置関係から長さを求める問題です。
図形問題で長さを求めるときに使うのは、ほとんどが合同か相似です。
ここでは相似で簡単に求まります。
ただ、計算がちょっとややこしく感じるかもしれませんね。
図形問題に取り組むときのポイントはわかっていますよね。
図を書いて、条件を書き込むことですよ。
このパターンはレポートで取り上げているので、ズバリ答えを導くのに直結する図を書いておきます。
いろいろな方法は考えられるでしょうがパッと浮かんだ図で突っ走ります。

\(\mathrm{DE}\) の延長と \(\mathrm{CB}\) の延長との交点を \(\mathrm{K}\) とすると、相似な三角形がたくさんあります。
どれを選んでも良いのですが、\(△\mathrm{CKD}\) と \(△\mathrm{HKF}\) と \(△\mathrm{HDG}\) を選びます。
その前にわかる長さを出しておきます。
三平方の定理から、
\(\mathrm{DK}=\sqrt{2^2+6^2}=\sqrt{40}=2\sqrt{10}\)
\(\displaystyle \mathrm{KE}=\sqrt{1^2+3^2}=\sqrt{10}=\frac{1}{2}\mathrm{DK}\)
さて、相似を利用しましょう。
ここからは図の中で処理したいのですが、たぶん理解できないと思うので説明を入れます。
図の中でやればむちゃくちゃ簡単にすむのですが、これが文章にすると難しく感じるんですよね。
\(△\mathrm{CKD}\) ∽ \(△\mathrm{HKF}\) ∽ \(△\mathrm{HDG}\)
で相似比は
\(△\mathrm{CKD}\) ∽ \(△\mathrm{HKF}\)
においては
\(\mathrm{KD:KF}=2\sqrt{10}:5\)
だから
\(\mathrm{CK:HK=6:HK}=2\sqrt{10}:5\)
より
\(\begin{eqnarray}
2\sqrt{10}\cdot \mathrm{HK}&=&6\times 5\\ \\
\displaystyle \mathrm{HK}&=&\frac{6\times 5}{2\sqrt{10}}\\ \\
&=&\displaystyle \frac{30\times \sqrt{10}}{2\sqrt{10}\times \sqrt{10}}\\ \\
&=&\displaystyle \frac{3\sqrt{10}}{2}
\end{eqnarray}\)
また \(△\mathrm{CKD}\) で \(\mathrm{CD:CK}=1:3\) なので
\(△\mathrm{HDG}\) において
\(\mathrm{GH}=\color{red}{x}\) とおくと \(\mathrm{DH}=\color{red}{3x}\)
ここまでをもう一度図に示しておくと、
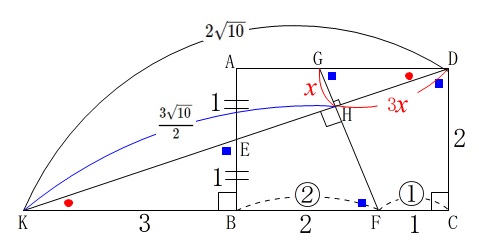
ここまで来れば簡単でしょう。
\(\mathrm{DH+HK=DK}\)
なので
\(\begin{eqnarray}
\displaystyle 3x+\frac{3\sqrt{10}}{2}&=&2\sqrt{10}\\
\displaystyle 6x+3\sqrt{10}&=&4\sqrt{10}\\
6x&=&4\sqrt{10}-3\sqrt{10}\\
6x&=&\sqrt{10}\\
\displaystyle x&=&\underline{\frac{\sqrt{10}}{6}}
\end{eqnarray}\)
求めたい長さを文字でおくと比例式が使えるので上の解法をしましたが、
DK の長さから HK の長さを引くことで DH をだして、
\(\displaystyle \mathrm{GH=\frac{1}{3}\times DH}\)
としても良いですよ。
図の中で見ていくとそれほど時間はかからないんだけど、
図を書いて説明するとなると大変なんですよ。
(イ)
割と長い日本語の文章で書いてありますが、文章の順序のままで数学の文章にしてしまえば良いだけです。
速さ、道のり、時間の関係は、線分図が活躍します。
家からバス停まで \(a\,\mathrm{km}\)
バス停から駅まで \(b\,\mathrm{km}\)
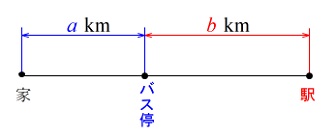
家からバス停まで 時速 \(4\,\mathrm{km}\)
バス停から駅まで 時速 \(30\,\mathrm{km}\)
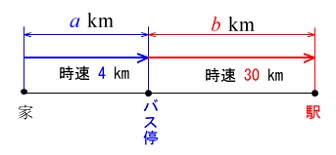
かかった時間は
家からバス停まで \(\displaystyle \frac{a}{4}\) (時間)
バス停から駅まで \(\displaystyle \frac{b}{30}\) (時間)
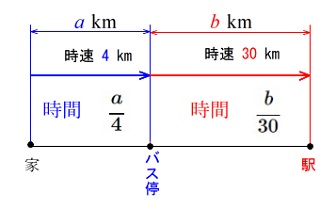
よって家から駅までかかった時間 \(t\) は
\(\displaystyle t=\frac{a}{4}+\frac{b}{30}\)
または
\(\displaystyle t=\frac{1}{4}a+\frac{1}{30}b\)
または
\(\displaystyle t=\frac{30a+4b}{120}\)
どの形でも減点はありません。
(採点基準に書いてありました。)
これだけで何点?5点です。
ところでこの文章題は、A さんでなくても誰でも良いのですよね?
そもそも A さんってだれ?
家とバス停じゃなくても駅じゃなくてもどこでも良いでしょう?
ということで問題のいらないところを削ってみると、
\(a\,\mathrm{km}\) の距離を時速 \(4\,\mathrm{km}\) で移動し、\(b\,\mathrm{km}\) の距離を時速 \(30\,\mathrm{km}\) で移動した。
合わせて \(t\) 時間かかった。
\(t\) を \(a\) と \(b\) を使って表しなさい。
となります。
ちょっと長くなりましたので、ここでいったん区切ります。
ちなみにここまで、49点の配点がされています。
「だから?」
知っていましたか。
だったら平均点 \(\color{magenta}{\fbox{56.0}}\) の意味もわかりますね。
⇒ 神奈川県公立高校入試2018(平成30年度)の数学問4の解説
問4は関数ですが面積比の問題があります。
分数の計算処理をうまくやらないと結構時間がかかるのではないでしょうか。
⇒ 神奈川県公立入試2018年(平成30年)の数学問5確率問題の解説
問5の確率問題の解き方です。
難しくはないので確率では何が必要なのか知っておきましょう。
⇒ 2018年度神奈川県公立高校入試の数学問6立体図形の考え方と解説
問6は立体(円すい)の問題です。
やってみれば、見たことある解法かもしれません。
⇒ 神奈川県公立高校入試2018の数学問7(平面図形)の解説
問7は平面に戻って証明です。
続き問題で証明内容を利用するのかと思っていたら意外でした。
神奈川県の数学過去問解説まとめページです。
