2019年度神奈川県公立高校入試の数学問6空間図形問題の解説

2019年度神奈川県で行われた公立高校入試の数学問題問6の空間図形問題の解説です。
三角柱の表面積、切り取った断面の三角形の面積、最短距離の3つの問題があります。
それほど時間はかからない基本問題ですので短時間で済ませておくと良いですね。

問題は神奈川県の公式サイトにもあります。

⇒　2019年度神奈川県立高校入試数学問題

問\(\,6\,\)

三角柱と長さや角度の条件がありますので書き出しておきます。

　\(\,\mathrm{AB}=3\,\)
　\(\,\mathrm{BC=4}\,\)
　\(\,\mathrm{∠ABC=90^{\circ}}\,\)
　\(\,\mathrm{AD=BE=CF=2}\,\)
　\(\,\mathrm{G}\,\)は\(\,\mathrm{EF}\,\)の中点

長さの単位は\(\,\mathrm{cm}\,\)ですが省略しています。

これらの条件を1つでも見逃すと答えまでたどり着けませんよ。
次にこれらの条件を図示します。

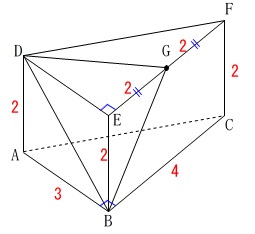他にも分かることはいろいろありますが問題の誘導に乗りましょう。

（ア）
三角柱の表面積を求めます。
表面積を求めるので展開図ですが、描き方によって見え方が違うので自分で見やすい図で良いですよ。
ここまでくると\(\,\mathrm{AC}\,\)の長さが欲しくなりますよね。

直角三角形\(\,\mathrm{△ABC}\,\)に三平方の定理を利用して、

　\(\begin{eqnarray}\displaystyle
\mathrm{AB^2+BC^2}&=&\mathrm{AC^2}\\
3^2+4^2&=&\mathrm{AC^2}\\
9+16&=&\mathrm{AC^2}\\
25&=&\mathrm{AC^2}\\
\pm 5&=&\mathrm{AC}
\end{eqnarray}\)

\(\,\mathrm{AC}\,\)は長さなので\(\,\mathrm{AC\,＞\,0}\,\)だから
　\(\mathrm{AC=5}\)
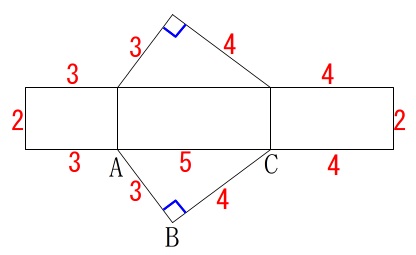表面積は2つの直角三角形と長方形の面積を合わせたものとなります。

　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 3\times 4\times 2+(3+4+5)\times 2\\
=12+24\\
=\underline{　36　}\)

（イ）
三角柱を平面で切り取った\(\,\mathrm{△BGD}\,\)の面積を求めます。
立体の切り口がどういう形になるのかは、ここでは説明不要ですね。

　『\(\,3\,\)点を結んでできる三角形の面積』

と問題に書いてあります。

立体は立体のまま考えない、というのは立体問題の基本です。
立体のまま位置関係がつかめる人は良いですけど、少なくとも私のような凡人は次元を下げて問題を少しでも簡単にしておきましょう。

\(\,\mathrm{△BGD}\,\)を抜き出してみます。
長さが1つも出ていません。

そこで長さを出すために違う面を抜き出します。

　\(\,\mathrm{BD}\,\)の長さを求めるために長方形\(\,\mathrm{ABED}\,\)
　\(\,\mathrm{BG}\,\)の長さを求めるために長方形\(\,\mathrm{BCFE}\,\)
　\(\,\mathrm{DG}\,\)の長さを求めるために三角形\(\,\mathrm{DEF}\,\)

をそれぞれ抜き出します。

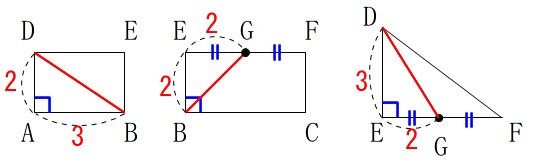
すべて直角三角形なので三平方の定理が使えます。

三平方の定理は使えると思うので直接辺の長さを出しておきます。

　\(\,\mathrm{BD=\sqrt{2^2+3^2}=\sqrt{13}}\,\)
　\(\,\mathrm{BG=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}}\,\)　
　\(\,\mathrm{DG=\sqrt{2^2+3^2}=\sqrt{13}}\,\)

このことから\(\,\mathrm{△BDG}\,\)は二等辺三角形だと分かります。

二等辺三角形の頂角の二等分線は底辺を垂直に二等分します。
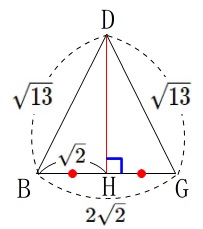\(\,\mathrm{△BDG}\,\)の高さは垂線\(\,\mathrm{DH}\,\)になります。

三平方の定理から

　\(\begin{eqnarray}
\mathrm{BH^2+DH^2}&=&\mathrm{BD^2}\\
(\sqrt{2})^2+\mathrm{DH^2}&=&(\sqrt{13})^2\\
2+\mathrm{DH^2}&=&13\\
\mathrm{DH^2}&=&13-2\\
\mathrm{DH^2}&=&11\\
\mathrm{DH}&=&\sqrt{11}　(\mathrm{DH}\,＞\,0)
\end{eqnarray}\)

底辺は\(\,\mathrm{BG=2\sqrt{2}}\,\)なので

　\(\begin{eqnarray}
\mathrm{△BDG}&=&\frac{1}{2}\times 2\sqrt{2}\times \sqrt{11}\\
&=&\underline{　\sqrt{22}　}
\end{eqnarray}\)

ここまでは基本通りやれば問題ないでしょう。

（ウ）
『最も短くなるように』引いた線の長さです。

数学で距離というのは最短距離のことを意味します。

ここでは面が変わるところで線が折れますが、
平面で見れば一直線になったときが最小となる距離になります。

展開図を利用しますがそのまま抜き出しても一筋では答えは出ません。
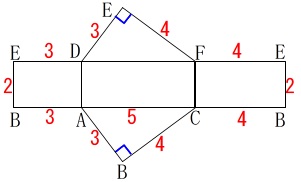表面積を求めた展開図ですが、これでは\(\,\mathrm{B}\,\)から辺\(\,\mathrm{EF}\,\)を経由して\(\,\mathrm{C}\,\)への一直線は書けません。

ちょっと並べ方をかえてみます。
いくつかありますのでどの並べ方が良いかは自分で探して下さい。
これは自分で試して見ないとどれが良いか実感できないところです。
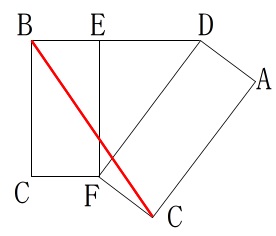これが見やすいと感じたのでこの部分的な展開図を使います。

これがクネクネしてたら最も短くなる線ではありません。
まっすぐな赤線が最短です。
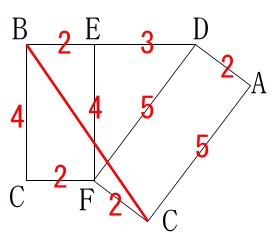出てきている長さを書き込んでみましたがすぐには求まりそうもありません。
ここでもいくつか線分を引いて試しますが、こういうときは、相似です。
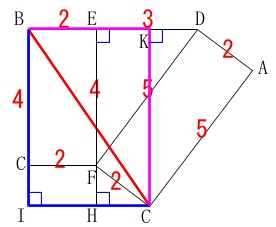\(\,\mathrm{△CKB}\,\)でも\(\,\mathrm{△BIC}\,\)でも良いのですが、
どちらにしても
　\(\,\mathrm{△FED}\,\)　∽　\(\,\mathrm{△CHF}\,\)
この相似を使って部分的な長さを出さなければなりません。
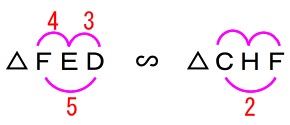相似比は\(\,\color{red}{5:2}\,\)です。

　\(\begin{eqnarray}\displaystyle
\mathrm{FD:CF}&=&\mathrm{FE:CH}\\
5:2&=&4:\mathrm{CH}\\
5\mathrm{CH}&=&8\\
\mathrm{CH}&=&\frac{8}{5}
\end{eqnarray}\)

また
　\(\begin{eqnarray}\displaystyle
\mathrm{FD:CF}&=&\mathrm{ED:HF}\\
5:2&=&3:\mathrm{HF}\\
5\mathrm{HF}&=&6\\
\mathrm{CH}&=&\frac{6}{5}
\end{eqnarray}\)
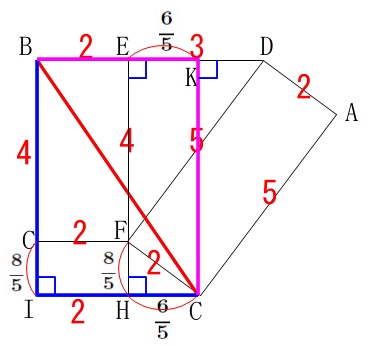三平方の定理から

　\(\begin{eqnarray}\displaystyle
\mathrm{BC^2}&=&\mathrm{BI^2+CI^2}\\
&=&\left(4+\frac{8}{5}\right)^2+\left(\frac{6}{5}+2\right)^2\\
&=&\left(\frac{4\times 5+8}{5}\right)^2+\left(\frac{6+2\times 5}{5}\right)^2\\
&=&\left(\frac{28}{5}\right)^2+\left(\frac{16}{5}\right)^2\\
&=&\frac{28^2+16^2}{5^2}\\
&=&\frac{676+324}{5^2}\\
&=&\frac{1000}{25}\\
&=&40
\end{eqnarray}\)

分母は\(\,5^2\,\)のままでも良かったのですが、分子が\(\,1000\,\)になったので\(\,25\,\)として割り算しました。

\(\,\mathrm{BC}\,\)は線分なので正の数だから

　\(\begin{eqnarray}
\mathrm{BC}&=&\sqrt{40}\\
&=&\underline{　2\sqrt{10}　}
\end{eqnarray}\)

これが最も短くなるように引いた線の長さです。

最短の長さは、直線です。

問6はこれで終わりですがまだあるんですよね。

⇒　2019年度神奈川県公立高校入試の数学問7平面図形問題の解説

問\(\,7\,\)は円周角の定理から相似の証明と線分の長さを求める問題です。

誘導がされているのでニコちゃんマークですぐに終わります。

⇒　2019年度神奈川県公立高校入試の数学問題問1,2の解説

問\(\,1,2\,\)の小問集合

⇒　2019年度神奈川県公立高校入試の数学問題問3の解説