2019年度東京都公立高校入試数学第4問平面図形問題の解説

2019年(平成31年)度東京都で行われた公立高校入試数学第4問の平面図形問題の解説です。
平行四辺形の定理から角度を求める問題と相似の証明および面積比を求める問題です。
面積比は長さが与えられていないので相似比をうまく使って部分的に面積比を出すと良いでしょう。

問題は東京都も公開してくれています。

⇒　2019年東京都公立高校入試前期の数学問題

　\(\color{black}{\fbox{　4　}}\)

〔問\(\,1\,\)〕

図\(\,1\,\)は平行四辺形です。

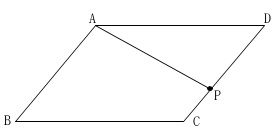
　\(\,\mathrm{∠ABC}=50^{\circ}\,\)
　\(\,\mathrm{∠DAP}=a^{\circ}\,\)

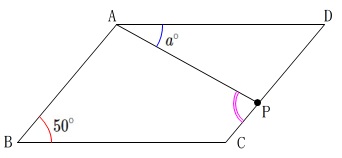
とするときの\(\,\mathrm{∠APC}\,\)の大きさを求めます。

平行四辺形の対角は等しいので
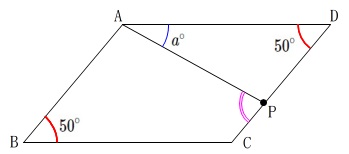よって、

　\(\begin{eqnarray}
\mathrm{∠APC}&=&\mathrm{\color{blue}{∠PAC}+\color{red}{∠PDA}}\\
&=&\underline{　(a+50)　度}
\end{eqnarray}\)

三角形の内角の和を使うより、

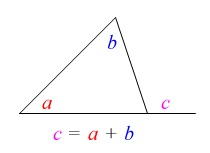
　『三角形の1つの外角は他の2つの内角の和に等しい。』

を使ったほうがはやいでしょう。

〔問\(\,2\,\)〕

図\(\,1\,\)の平行四辺形に条件が加わります。

　\(\,\mathrm{BP}\,\)　∥　\(\,\mathrm{QD}\,\)
　\(\,\mathrm{AP}\,\)と\(\,\mathrm{QD}\,\)の交点を\(\,\mathrm{R}\,\)
①はこのとき\(\,\mathrm{△ABP}\,\)　∽　\(\,\mathrm{△PDR}\,\)を証明します。

証明するときは図の中で先に証明を済ませておくことがポイントです。
図の中で証明できていないのに証明が書けるはずありません。
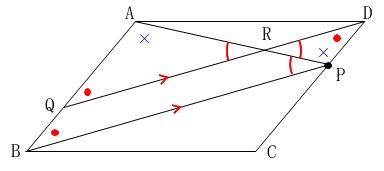相似ですね。

　四角形\(\,\mathrm{ABCD}\,\)は平行四辺形なので
　　\(\,\mathrm{AB}\,\)　∥　\(\,\mathrm{DC}\,\)
平行線の錯角は等しくなるので
　　\(\,\mathrm{∠BAP=∠DPA}\,\)　･･･①
　　\(\,\mathrm{∠AQD=∠PDR}\,\)　･･･②
また、
　\(\,\mathrm{BP}\,\)　∥　\(\,\mathrm{QD}\,\)
なので同位角は等しくなるから
　　\(\,\mathrm{∠AQD=∠ABP}\,\)　･･･③

　\(\,\mathrm{△ABP}\,\)と\(\,\mathrm{△PDR}\,\)において、
①より
　\(\,\mathrm{∠BAP=∠DPR}\,\)　･･･④
また、②③より
　\(\,\mathrm{∠ABP=∠PDR}\,\)　･･･⑤
④⑤より
　\(\,2\,\)組の角がそれぞれ等しいので
　\(\,\mathrm{△ABP}\,\)　∽　\(\,\mathrm{△PDR}\,\)（終わり）

証明は良いですが、これを②でどう使いこなすかです。
①で証明したことを②で使うのが普通ですよ。

使わない問題もありますが、この問題は誘導してくれています。

②で加わる条件を先に書いておきましょう。

　\(\,\mathrm{CR}\,\)と\(\,\mathrm{BP}\,\)の交点を\(\,\mathrm{S}\,\)
　\(\,\mathrm{CP:PD=2：1}\,\)

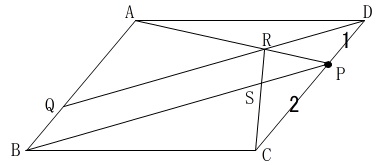
　\(\,\mathrm{△ABP}\,\)　∽　\(\,\mathrm{△PDR}\,\)
において相似比は\(\,3:1\,\)です。

また
　\(\,\mathrm{△AQR}\,\)　∽　\(\,\mathrm{△PDR}\,\)
でもあり相似比は\(\,\color{red}{2:1}\,\)です。

さらに\(\,\mathrm{BP}\,\)　∥　\(\,\mathrm{QD}\,\)なので
　\(\,\mathrm{△CPS}\,\)　∽　\(\,\mathrm{△CDR}\,\)
で、相似比は\(\,\color{blue}{2：3}\,\)です。

これらを線分比として図に書き込みますが、
値は長さではなく比のことで、色分けしている数字が対応する線分比と見て下さい。
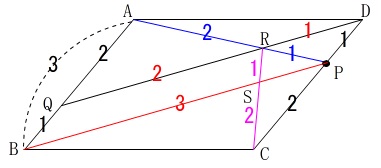これですべての部分の面積比が出ます。

\(\,\mathrm{△CPS}\,\)と\(\,\mathrm{△CDR}\,\)の相似比が\(\,2:3\,\)なので、
\(\,\mathrm{DR:SP=3:2}\,\)も分かりますが、
\(\,\mathrm{DR}\,\)を\(\,1\,\)としているので分数になるし使わなくても出せるので書いていません。

長さがないので面積を適当に決めて良いのですが、
四角形\(\,\mathrm{ABCD}\,\)の面積を\(\,1\,\)としておきます。
なくても分かるのですが分かり易くするために平行線を入れておきました。

相似比からこの平行線は\(\,\mathrm{AB}\,\)と\(\,\mathrm{DC}\,\)を\(\,3\,\)等分していることが分かります。

この図の部分部分の面積をバラッバラにして、
全部出しても良いのですがも良いのですが、笑
時間がもったいないので必要な部分だけにしておきます。

分かり易い\(\,\mathrm{△AQR}\,\)の面積から出しておきましょう。
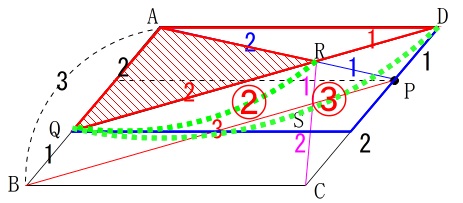平行四辺形\(\,\mathrm{ABCD}\,\)を圧縮してい行きます。

\(\,\mathrm{ABCD}\,\)を\(\displaystyle \color{blue}{\frac{2}{3}}\,\)に圧縮した平行四辺形の半分が\(\,\mathrm{\color{red}{△AQD}}\,\)で、
それを\(\,2：1\,\)に底辺を分けているので、

　\(\begin{eqnarray}
\mathrm{\color{red}{△AQR}}&=&\color{red}{1}\times \color{blue}{\frac{2}{3}}\times \frac{1}{2}\times \frac{2}{3}\\
&=&\color{red}{\frac{2}{9}}　･･･\color{blue}{①}
\end{eqnarray}\)

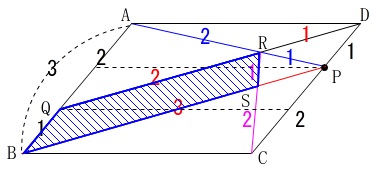今度は四角形\(\,\mathrm{\color{blue}{QBSR}}\,\)の面積です。

何が問題って、\(\,\mathrm{△PRS}\,\)ですね。

　\(\displaystyle \mathrm{△ABP=\frac{1}{2}}\,\)
だから
　\(\begin{eqnarray}\displaystyle
四角形\mathrm{QBPR}&=&\mathrm{△ABP-\color{red}{△AQR}}\\
&=&\frac{1}{2}-\color{red}{\frac{2}{9}}\\
&=&\frac{9-2\times 2}{18}\\
&=&\frac{5}{18}
\end{eqnarray}\)

と、求めることはできますが\(\,\mathrm{△PRS}\,\)は必要ない部分なのです。

つまり\(\,\mathrm{△PRS}\,\)を求めて引けば良いだけです。

ところで、
\(\displaystyle \mathrm{△ABP=\frac{1}{2}}\,\)を求める部分ですが、

\(\,\mathrm{△AQR}\,\)と\(\,\mathrm{△ABP}\,\)は相似で、
　相似比が\(\,2：3\,\)
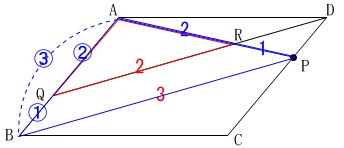なので
　面積比は\(\,2^2:3^2=4：9\,\)

　\(\displaystyle \mathrm{△AQR=\color{red}{\frac{2}{9}}}\,\)
だから
　\(\begin{eqnarray}\displaystyle
4:9&=&\frac{2}{9}:\mathrm{△ABP}\\
4\times \mathrm{△ABP}&=&9\times \frac{2}{9}\\
\mathrm{△ABP}&=&\frac{1}{2}
\end{eqnarray}\)

とするのはムダですよ。

\(\,\mathrm{△ABP}\,\)は平行四辺形\(\,\mathrm{ABCD}\,\)の半分です。

誰もやらないか？笑

では\(\,\mathrm{△PRS}\,\)を求めましょう。
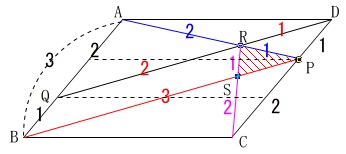ズバッと、
　\(\displaystyle \mathrm{△PRS}=\frac{1}{2}\times \frac{1}{3}\times \frac{2}{3}\times \frac{1}{3}\)
とやりたいところですが、解説になってませんよね？　

順を追って説明します。

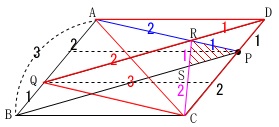どこからと決まっているわけではありませんが、\(\,\mathrm{△PRS}\,\)に絞れるように三角形を縮めていきます。

\(\,\mathrm{\color{red}{△CQD}}\,\)を始まりにします。

　\(\displaystyle \mathrm{\color{red}{△CQD}=\frac{1}{2}}\,\)

\(\,\mathrm{QR:RD=2:1}\,\)なので

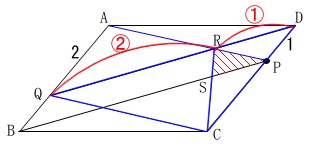
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△CRD}}&=&\frac{1}{3}\times \mathrm{\color{red}{△CQD}}\\
&=&\frac{1}{3}\times \frac{1}{2}
\end{eqnarray}\)

途中の計算はしなくて良いですよ。
最後に約分できることがあるのでそのままで良いです。
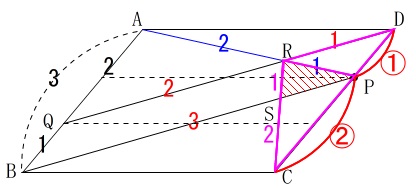次に\(\,\mathrm{CP:PD=2:1}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{magenta}{△CPR}}&=&\frac{2}{3}\times \mathrm{\color{blue}{△CRD}}\\
&=&\frac{2}{3}\times \frac{1}{3}\times \frac{1}{2}
\end{eqnarray}\)
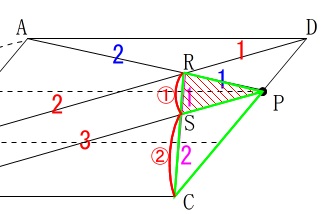いよいよです。

　\(\begin{eqnarray}\displaystyle
\mathrm{△PRS}&=&\frac{1}{3}\times \mathrm{△CPR}\\
&=&\frac{1}{3}\times \frac{2}{3}\times \frac{1}{3}\times \frac{1}{2}\\
&=&\frac{1}{27}
\end{eqnarray}\)

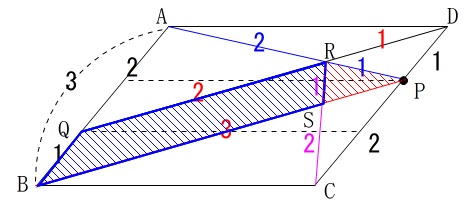
四角形\(\,\mathrm{\color{blue}{QBSR}}\,\)は、
四角形\(\,\mathrm{QBPR}\,\)から\(\,\mathrm{△PRS}\,\)を引いたものです。

　\(\displaystyle 四角形\mathrm{QBPR}=\frac{5}{18}\)
　\(\displaystyle △\mathrm{PRS}=\frac{1}{27}\)
なので
　\(\begin{eqnarray}\displaystyle
四角形\,\mathrm{\color{blue}{QBSR}}&=&四角形\,\mathrm{QBPR}\,-\mathrm{△PRS}\\
&=&\frac{5}{18}-\frac{1}{27}\\
&=&\frac{5\times 3-1\times 2}{54}\\
&=&\color{red}{\frac{13}{54}}　･･･\color{blue}{②}
\end{eqnarray}\)

よって\(\,\color{blue}{①}\,\)と\(\,\color{blue}{②}\,\)から

　\(\begin{eqnarray}\displaystyle
\frac{　四角形\mathrm{QBSR}　}{　\mathrm{△AQR}　}&=&\frac{13}{54}\div \frac{2}{9}\\
&=&\frac{13}{54}\times \frac{9}{2}\\
&=&\underline{　\frac{13}{12}　}　倍
\end{eqnarray}\)

もっと楽な方法はあります。

例えば、\(\displaystyle \,\mathrm{RD:SP=1:\color{red}{\frac{2}{3}}}\,\)としておけば、

　\(\begin{eqnarray}\displaystyle
\mathrm{△PRS}&=&\mathrm{△ABP}\times \frac{1}{3}\times \frac{\frac{2}{3}}{3}\\
&=&\frac{1}{2}\times \frac{1}{3}\times \frac{2}{9}\\
&=&\frac{1}{27}
\end{eqnarray}\)