2019年度東京都公立高校入試数学第5問立体問題の解説

2019年(平成31年)度東京都で行われた公立高校入試数学第5問の立体問題の解説です。
立体は三角すいで、三角すい中の線分の長さと体積を求める問題の２つがあります。
点Pは動点を表していますが、固定された点で考えれば良いだけなので割と簡単に答えが出る問題です。

問題は東京都も公開してくれています。

⇒　2019年東京都公立高校入試前期の数学問題

　\(\color{black}{\fbox{　5　}}\)

この問題（立体）はやることが決まっていて、確認程度で終わると思えるので簡単に済ませます。

問に入る前に与えられた条件はすべての問題に通じる条件です。

　\(\color{red}{\fbox{　条件　}}\)

　\(\,\mathrm{ＡＢ=9}\,\)
　\(\,\mathrm{ＢＣ＝ＢＤ＝ＣＤ＝6}\,\)
　\(\,\mathrm{∠ABC=∠ABD=90^{\circ}}\,\)
　\(\,\mathrm{P}\,\)は\(\,\mathrm{ＣＤ}\,\)上の点
　\(\,\mathrm{Q}\,\)は\(\,\mathrm{ＡＢ}\,\)上にある点

〔問\(\,1\,\)〕

条件が加わります。

　点\(\,\mathrm{P}\,\)が\(\,\mathrm{ＣＤ}\,\)の中点
　\(\,\mathrm{AQ=6}\,\)

このときの\(\,\mathrm{PQ}\,\)の長さを求めます。

点\(\,\mathrm{P,Q}\,\)ともに固定されているので長さも固定されます。

\(\,\mathrm{P,Q}\,\)を含む面を抜き出しましょう。
立体のまま考えられる人は立体のまま考えて良いですけど、問題を簡単にしたいなら面を抜き出せば良いです。

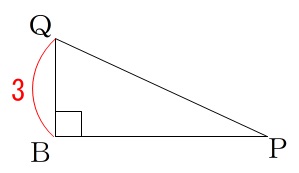
\(\,\mathrm{△BPQ}\,\)を抜き出すと、\(\,\mathrm{PQ}\,\)を求めたいので\(\,\mathrm{BP}\,\)が必要になります。
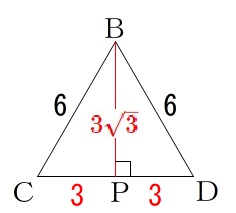\(\,\mathrm{△BCD}\,\)は正三角形なので、三平方の定理でも三角定規の比でも良いですが、

　\(\mathrm{BP}=\color{red}{3\sqrt{3}}\)
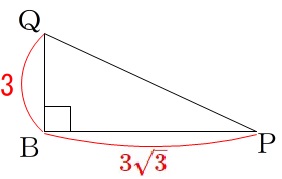三平方の定理から

　\(\begin{eqnarray}
\mathrm{PQ^2}&=&\mathrm{BQ^2+BP^2}\\
&=&(3)^2+(3\sqrt{3})^2\\
&=&9+27\\
&=&36\\
\mathrm{PQ}&=&\pm 6
\end{eqnarray}\)

\(\,\mathrm{PQ}\,\)は長さだから\(\,\mathrm{PQ\,＞\,0}\,\)なので
　
　\(\mathrm{PQ}=\underline{　6　}\)

〔問\(\,2\,\)〕

条件が〔問\(\,1\,\)〕とは変わります。

　点\(\,\mathrm{P}\,\)は点\(\,\mathrm{C}\,\)と一致
　点\(\,\mathrm{R}\,\)は\(\,\mathrm{AD}\,\)の中点
　\(\,\mathrm{AQ=8}\,\)
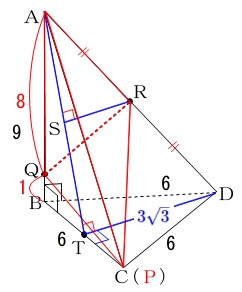
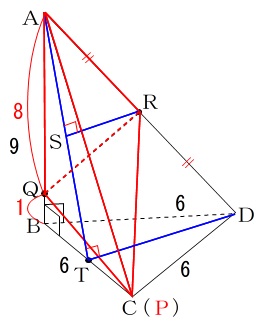立体\(\,\mathrm{R-AQP}\,\)は、
　底面が\(\,\mathrm{△AQP}\,\)
　高さが\(\,\mathrm{R}\,\)から\(\,\mathrm{△AQP}\,\)に下ろした垂線\(\,\mathrm{RS}\,\)の長さ
なので
　\(\,\mathrm{TD}\,\)は\(\,\mathrm{△ABC}\,\)の高さ〔問\(\,1\,\)〕の\(\,\mathrm{BP}\,\)に等しく、
　\(\,\mathrm{TD=3\sqrt{3}}\,\)
であることから
　\(\displaystyle \mathrm{SR}=\frac{1}{2}\times \mathrm{TD}=\frac{3\sqrt{3}}{2}\)
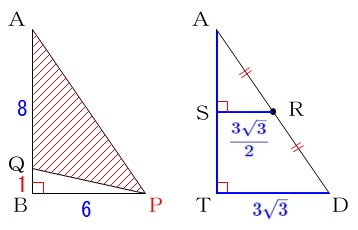よって求める体積は、
　\(\begin{eqnarray}
(立体\mathrm{R-AQP})&=&\frac{1}{3}\times \mathrm{△AQP}　\times \mathrm{RS}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 8\times 6\times \frac{3\sqrt{3}}{2}\\
&=&\underline{　12\sqrt{3}　}
\end{eqnarray}\)

この求め方で普通なので良いです。
元の三角すいの体積が
　\(\begin{eqnarray}
(三角すい\mathrm{A-BCD})&=&\frac{1}{3}\times \mathrm{△BCD}\times \mathrm{AB}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 6\times 3\sqrt{3}\times 9\\
&=&\color{magenta}{27\sqrt{3}}
\end{eqnarray}\)

問題の条件は
　\(\,\mathrm{AB:AQ=9:8}\,\)
　\(\,\mathrm{AD:AR=2:1}\,\)
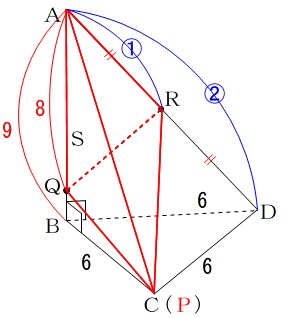なので\(\,\mathrm{AP=AC}\,\)であることだけ注意して、
　\(\begin{eqnarray}
(立体\mathrm{R-AQP})&=&\color{magenta}{27\sqrt{3}}\times \color{red}{\frac{8}{9}}\times \color{blue}{\frac{1}{2}}\times \frac{1}{1}\\
&=&\underline{　12\sqrt{3}　}
\end{eqnarray}\)