2019年(平成31年)度に北海道で行われた公立高校入試裁量問題第5問の解説です。
第5問は比例関数と図形の性質を融合させた問題や、
データ（資料）の度数分布表から平均値を求めるときの手順がしっかり理解できているかの確認問題です。
どちらも小問ではなく誘導がされているのでうまく条件を使えば良いように問題作成されています。
問題は北海道も公開してくれていますので正答とともに確認してください。
\(\large{\color{black}{\fbox{ 5 }}}\)
一般入試問題と違うのはこの\(\color{black}{\fbox{5}}\)だけです。
問\(\,1\,\)は比例関数と図形の性質の融合、
問\(\,2\,\)は資料（データ）の別問題なのでそれぞれの問題の条件をしっかり読み取りましょう。
問\(\,1\,\)の条件
点\(\,\mathrm{A}\,\)は\(\displaystyle \,y=\frac{12}{5}x\, ･･･①\)上の点
\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,5\,\)
\(\,\mathrm{A}\,\)から\(\,x\,\)軸に垂線を引いて\(\,x\,\)軸との交点を\(\,\mathrm{B}\,\)
(1)線分\(\,\mathrm{OA}\,\)の長さを求めます。
\(\,\mathrm{△OAB}\,\)は直角三角形なので三平方の定理が使えます。
線分\(\,\mathrm{OB}\,\)は\(\,\mathrm{A,B}\,\)の\(\,x\,\)座標なので長さは\(\,5\,\)ですが、
まだ線分\(\,\mathrm{AB}\,\)を出していません。
線分\(\,\mathrm{AB}\,\)は\(\,\mathrm{A}\,\)の\(\,y\,\)座標になるので、
①に\(\,x=5\,\)を代入して
\(\begin{eqnarray}
y&=&\frac{12}{5}\times (5)\\
&=&12
\end{eqnarray}\)
これから\(\,\mathrm{A}\,\)の座標は\(\,(\,5\,,\,12\,)\,\)なので
\(\,\mathrm{AB=12}\,\)
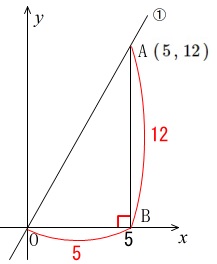三平方の定理から
\(\begin{eqnarray}
\mathrm{OA^2}&=&\mathrm{OB^2+AB^2}\\
&=&5^2+12^2\\
&=&25+144\\
&=&169\\
\mathrm{OA}&=&\pm 13
\end{eqnarray}\)
\(\,\mathrm{OA\,＞\,0}\,\)なので
\(\mathrm{OA}=\underline{ 13 }\)
\(\,169\,\)は素数の平方数なので素因数分解がすぐにはできないかもしれません。
裁量問題を受験すると決めている時点で練習の中で覚えていると思いますが、
平方数はある程度覚えておくと良いですよ。
(2)直線の式を求めますが、原点を通るので比例関数です。
条件は\(\,\mathrm{△OAB}\,\)については変わらず、
点\(\,\mathrm{C,D}\,\)が加わります。
\(\,\mathrm{C}\,\)は線分\(\,\mathrm{AB}\,\)上の点
\(\,\mathrm{D}\,\)は線分\(\,\mathrm{OA}\,\)上の点
\(\,\mathrm{∠ADC=90°}\,\)
\(\,\mathrm{AD=3}\,\)
これを図に書き込みます。
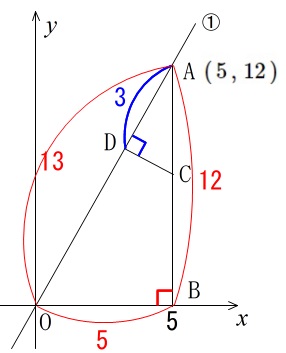
このとき\(\,\mathrm{∠OAB}\,\)が共通になるので
\(\,\mathrm{△OAB}\,\) ∽ \(\,\mathrm{△CAD}\,\)
（両方が直角三角形です。）
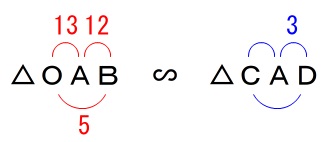
これから
\(\begin{eqnarray}\displaystyle
\mathrm{OA:CA}&=&\mathrm{AB:AD}\\
13:\mathrm{CA}&=&12:3\\
12\times \mathrm{CA}&=&3\times 13\\
\mathrm{CA}&=&\frac{3\times 13}{12}\\
&=&\color{magenta}{\frac{13}{4}}
\end{eqnarray}\)
このとき
\(\begin{eqnarray}
\mathrm{BC}&=&\mathrm{AB-AC}\\
&=&12-\frac{13}{4}\\
&=&\frac{12\times 4-13}{4}\\
&=&\frac{48-13}{4}\\
&=&\color{magenta}{\frac{35}{4}}
\end{eqnarray}\)
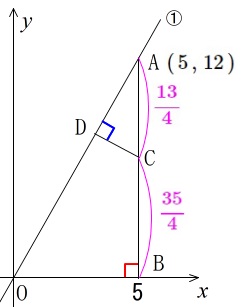
となるので\(\,\mathrm{C}\,\)の座標は\(\,x\,\)座標が\(\,5\,\)だから
\(\displaystyle \,\mathrm{C\,\left(\,5\,,\,\frac{35}{4}\,\right)}\,\)
直線\(\,\mathrm{OC}\,\)の傾き（比例定数）は
\(\begin{eqnarray}\displaystyle
\mathrm{\frac{BC}{OB}}&=&\frac{\color{magenta}{\frac{35}{4}}}{\color{blue}{5}}\\
&=&\color{magenta}{\frac{35}{4}}\div \color{blue}{5}\\
&=&\color{magenta}{\frac{35}{4}}\times \color{blue}{\frac{1}{5}}\\
&=&\frac{7}{4}
\end{eqnarray}\)
よって求める直線の式は
\(\displaystyle \,\underline{ y=\frac{7}{4}x }\,\)
変化の割合を求めるときに分数が処理しにくい人は、
割り算は逆数のかけ算
に変えて計算すれば分かり易いですよ。
問\(\,2\,\)
\(\,\mathrm{A}\,\)中学校とかバスケットボール部とかは問題に関係ありません。
\(\,24\,\)人の握力についての調査で度数分布表がありますがポイントは1つだけです。
度数分布表では同じ階級にいる人の値は、
『すべてその階級値と見なす』
ということです。
だからこの表では一番右の
\(\,(階級値)\times (度数)\,\)の合計\(\,720\,\)
が総得点（ここでは握力の合計）となります。
(1)
\(\displaystyle \,(平均値)=\frac{ (総得点) }{ (度数合計) }\,\)
なので
\(\begin{eqnarray}\displaystyle
(平均値)&=&\frac{720}{24}\\
&=&\underline{ 30 } (\mathrm{kg)}
\end{eqnarray}\)
(2)度数分布表中の度数\(\color{black}{\fbox{ ア }}\)、\(\color{black}{\fbox{ イ }}\)を求めます。
\(\color{black}{\fbox{ ア }}\)、\(\color{black}{\fbox{ イ }}\)のままだと書きにくいので、
\(\color{black}{\fbox{ ア }}=x\)
\(\color{black}{\fbox{ イ }}=y\)
とおきます。
度数合計が\(\,24\,\)なのでそれぞれの階級を合計から
\(\begin{eqnarray}
3+x+y+2+1&=&24\\
x+y&=&18 ･･･①
\end{eqnarray}\)
またこのとき\(\,(階級値)\times (度数)\,\)は
\(\,10～20\,\)の階級では\(\,15\times 3=45\,\)
\(\,20～30\,\)の階級では\(\,25\times x=25x\,\)
\(\,30～40\,\)の階級では\(\,35\times y=35y\,\)
\(\,40～50\,\)の階級では\(\,45\times 2=90\,\)
\(\,50～60\,\)の階級では\(\,55\times 1=55\,\)
なのでこの合計が\(\,720\,\)であることから
\(\begin{eqnarray}
45+25x+35y+90+55&=&720\\
25x+35y+190&=&720\\
25x+35y&=&720-190\\
&=&530\\
5x+7y&=&106 ･･･②
\end{eqnarray}\)
①②から
\(\,x=10\,,\,y=8\,\)
答え \(\color{black}{\fbox{ ア }}\) \(\,\underline{ 10 }\,\) \(\color{black}{\fbox{ イ }}\) \(\,\underline{ 8 }\,\)
(3)
\(\,1\,\)年生\(\,6\,\)人のデータが加わります。
\(\,6\,\)人の値は同じ階級に入る
加えた後の\(\,30\,\)人の平均値は\(\,29\,\mathrm{kg}\)
このとき加わった\(\,6\,\)人はどこの階級なのかを求めます。
\(\,6\,\)人は同じ階級に入るので、
5つの階級に\(\,6\,\)人を加えた場合をそれぞれ調べても階級は出ます。
しかし、解答の空欄をうめるように誘導がついているので総得点から考えていくことになります。
これまでに出てきた数値を度数分布表に入れておきます。
\(\begin{array}{|c|c|c|} \hline
階級値\color{blue}{a} & 度数\color{magenta}{b} & \color{blue}{a}\times \color{magenta}{b} \\ \hline
15 & 3 & 45 \\ \hline
25 & 10 & 250 \\ \hline
35 & 8 & 360 \\ \hline
45 & 2 & 90 \\ \hline
55 & 1 & 55 \\ \hline
& 24 & \color{red}{720} \\ \hline
\end{array}\)
(1)で度数合計\(\,24\,\)と総得点の\(\,\color{red}{720}\,\)から平均値が出ました。
同じように、問題に書いてある
『\(\,30\,\)人の平均値は\(\,29\,\mathrm{kg}\)』
から総得点は
\(\,30\times 29=\color{red}{870}\,\)
この総得点の差は\(\,6\,\)人の得点となることから解答欄をうめていきます。
（解答）
\(\,30\,\)人の握力の平均値が\(\,29\,\mathrm{kg}\,\)であることから、
\(\,30\,\)人の(階級値)×(度数)の合計は、
（ここから）
\(\,30\times 29=\color{red}{870}\,\)
となる。
\(\,24\,\)人のときの(階級値)×(度数)の合計が\(\,720\,\)なので
この差
\(\,870-720=\color{red}{150}\,\)
は\(\,6\,\)人の階級値の合計になる。
\(\,6\,\)人が同じ階級に入るので階級値は
\(\displaystyle \frac{150}{6}=\color{red}{25} \,(\mathrm{kg})\)
よって、\(\,1\,\)年生\(\,6\,\)人の握力が入った階級は
\(\,\mathrm{20 kg}\,\)以上\(\,\mathrm{30 \mathrm{kg}}\,\)未満の階級
（ここまで）
途中の日本語は違っていてもかまいません。
赤い数字にしてある値が書いてあれば部分点を与えてくれます。
ただし、この問題は階級を求める、ので階級値で止まってはダメですよ。
問題はよく読んで、何を答えるのかは間違えないようにしましょう。
2019年北海道公立入試裁量問題は以上です。
珍しく立体、空間図形からの平面の抜き出しがないセットでしたね。
（体積を求める問題はありました。）
来年はきっと出る。笑
なんて山を張ると公立入試では失敗します。
中学数学全般の習得度合いを測るのが公立高校入試の目的の1つです。
選抜するための裁量問題ですが、基本の組み合わせで応用している、ということは全国的に変わりませんよ。
⇒ 2019年度北海道公立入試裁量問題の解説 第1,2問(一般第2,3)
もう一度最初から裁量問題を見通してみてください。
中学\(\,1\,\)年から\(\,3\,\)年までの内容がまんべんなく出題されていることが分かります。
数年分見ておくと傾向ははっきりします。
問題内容は変わりますが、問題の難易度が大きく変わるということは少ないです。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
