1次関数とは？傾きや切片、変域などの用語と関数の増加減少

1次関数とはどのような形の関数をいうのか、また傾きや切片および変域などの用語を確認しておきましょう。
中学であつかう関数は4つだけですが、3年で習う2次関数（放物線）を除いた、
比例、反比例の関数とともに1次関数の増加、減少の仕方を見ておきます。

1次関数とは？傾きと切片

中学生、高校生が苦手にする関数ですが、
関数と言っても中学校の間は、４つしか学習しません。

１年生のときにやった、
　「比例」：　\( \color{red}{y=ax}\)
「反比例」:　\(\displaystyle \color{red}{y=\frac{a}{x}}\)

２年生の今から勉強する「\(\,1\,\)次関数」、
３年生で学習する「\(\,\color{magenta}{y=ax^2}\,\)　(\(\,y\,\)が\(\,x\,\)の２乗に比例する関数）」
だけです。

そして、「比例」はこれから勉強する\(\,1\,\)次関数の特別な形だと分かります。
だから正確には３つなのです。

ということで、「\(\,1\,\)次関数とは？」、から入りましょう。

\(\,1\,\)次関数とは、\(\,y\,\)が\(\,x\,\)の\(\,1\,\)次式で表される関数のことを言います。

関数の式は\(\,y=\color{red}{a}x+\color{blue}{b}\,\)という形で表されます。

このとき\(\,\color{red}{a=0}\,\)のときは\(\,1\,\)次関数とはいいませんので注意しましょう。

この形で\(\,\color{blue}{b=0}\,\)のとき「比例」です。

\(\,1\,\)次関数はグラフで表すと必ず直線になります。
※
だからといって直線だから\(\,1\,\)次関数かといえばそうではありませんが、それはグラフの説明のときに詳しくします。

\(\,1\,\)次関数　\(\,y=\color{red}{a}x+\color{blue}{b}\,\)の
　\(\,\color{red}{a}\,\)を『傾き』
　\(\,\color{blue}{b}\,\)を『切片』
と呼びます。

これは覚えておかなければどうしようもない単語ですので覚えておきましょう。

ところで、
　比例の\(\,y=\color{red}{a}x\,\)
　反比例の\(\displaystyle \,y=\frac{\color{red}{a}}{x}\,\)
まだ習っていない人も多いでしょうけど、
　\(\,y\,\)が\(\,x\,\)の\(\,2\,\)乗に比例する\(\,y=\color{red}{a}x^2\,\)
の\(\,\color{red}{a}\,\)はすべて『比例定数』といいますので忘れないでください。

\(\,y=ax^2\,\)はまだあつかっていない段階での関数の性質を問題の中で見ておきましょう。

(1)
『\(\,y\,\)が\(\,x\,\)の\(\,1\,\)次関数である。』のは
　\(\,y=ax+b\,\)
つまり\(\,y\,\)が\(\,x\,\)の\(\,1\,\)次式で表されているものを選べば良いだけです。

　①\(\,y=x+6\,\)は\(\,x\,\)の\(\,1\,\)次式
　②\(\,y=2x+3\,\)は\(\,x\,\)の\(\,1\,\)次式
　③\(\displaystyle \,y=\frac{a}{x}\,\)は分母に\(\,x\,\)の\(\,1\,\)次式がありますが\(\,1\,\)次式とはいいません。
　④\(\,y=-3x+6\,\)は\(\,1\,\)次式

③は反比例です。

　答え　\(\,\underline{　①\,②\,④　}\,\)　

例えば\(\,y=3x\,\)や\(\displaystyle \,y=-\frac{1}{3}x\,\)も比例ですが、\(\,1\,\)次式ですよ。

1次関数の増加と減少

(2)
『\(\,x\,\)の値が増加するとき、対応する\(\,y\,\)の値も増加する。』

\(\,x\,\)が増えたとき、\(\,y\,\)も増えるのは、
　『傾き』が正のとき
です。

つまり、\(\,y=\color{red}{a}x+b\,\)　の　\(\,\color{red}{a}\,\)　が正のときです。

\(\,1\,\)次関数\(\,y=ax+b\,\)は直線で、

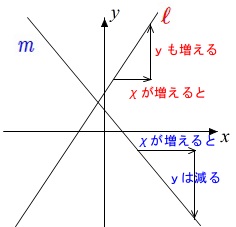
　\(\,\color{red}{\ell}\,\)のように右上がりになるのは、傾き\(\,a\,\)が正のとき、

　\(\,\color{blue}{m}\,\)のように右下がりになるのは、傾き\(\,a\,\)が負のとき、

なのです。

だから、答えは、\(\,\underline{　①　と　②　}\,\)

　④は傾きが負だから、右下がりとなって、

\(\,x\,\)が増える（増加する）と\(\,y\,\)は減る（減少する）からダメです。

　③　は反比例で、

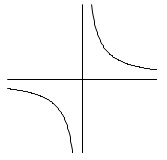
図のようになるから、
マイナス側でも、プラス側でも、\(\,x\,\)が増えると\(\,y\,\)は減ります。

座標の軸は\(\,x\,\)軸は右に大きくなるように、\(\,y\,\)軸は上に大きくなるように取ります。
このことは絶対ではありませんが何もことわりがなければ数学では約束事のようなものです。

なので、　
　「\(\,x\,\)が増える」（\(\,x\,\)が増加する）
というのは、
　座標上で考えると「右に動く」
ということです。数直線と同じです。

同じように、
　「\(\,y\,\)が増える」（\(\,y\,\)が増加する）
というのは、
　座標上で「上に動く」
ということで、逆に
　「\(\,y\,\)が減る」（\(\,y\,\)が減少する）
というのは、
　座標上で「下に動く」
ということです。

1次関数のグラフと変域

(3)
『グラフが\(\,y\,\)軸上の同じ点を通る。』

　「\(\,y\,\)軸上の同じ点を通る」
ということは、
　「切片が同じ」
ということです。

もともと「切片」というのは「\(\,y\,\)切片」とも言い、\(\,y\,\)軸との交点を意味します。
\(\,x\,\)軸との交点を\(\,x\,\)切片といいますが、中学では使いません。

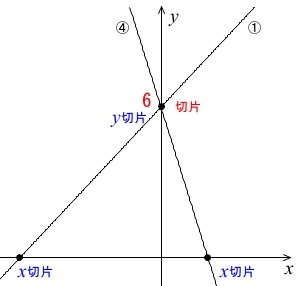
　①\(\,y=x\color{red}{+6}\,\)
　②\(\,y=2x+3\,\)
　③\(\displaystyle \,y=\frac{a}{x}\,\)
　④\(\,y=-3x\color{red}{+6}\,\)

切片（\(\,y\,\)切片）が同じなのは、\(\,\underline{　①　と　④　}\,\)　です。これが答え。

(4)
『\(\,x\,\)の変域が\(\,0\,≦\,x≦\,2\,\)のとき、\(\,y\,\)の変域は\(\,0\,≦\,y\,≦\,6\,\)』
になる関数を選びます。

「変域」というのは、\(\,x\,\)や\(\,y\,\)の動く範囲のことです。

高校になると、\(\,x\,\)の動く範囲を「定義域」、\(\,y\,\)の動く範囲を「値域」といいますが、中学の間は「変域」という言葉しか出てきません。

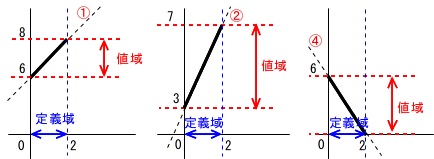
　\(\,x\,\)の変域（定義域）：\(\,0\,≦\,x\,≦\,2\,\)
　\(\,y\,\)の変域（値域）：\(\,0\,≦\,y\,≦\,6\,\)

となっています。

ここで注意して欲しいのは、\(\,x=0\,\)のとき、\(\,y=0\,\)になっているとは限らない、ということ。

変域の左端と左端、右端と右端が一致しない場合があるということです。

どうすればいいかというと、グラフを書いて確認すれば良いだけです。
きれいなグラフは必要ありませんが、グラフを書いて確認する、というのは関数をあつかう限りした方が良いですよ。

関数が苦手といいますが、すべて式や値だけで処理できると思っていることに原因があるのです。
高校生になるともっとはっきりしてきますよ。

　(グラフの\(\,x\,\)軸方向と\(\,y\,\)軸方向の縮尺は違います。）

③のグラフを省いたのは、③は反比例だから、\(\,x=0\,\)になることはないし、\(\,y=0\,\)になることもないからです。
（近づきはしますが、近づく、と値を取ることは違います。）

この\(\,0≦x≦2\,\)の範囲で\(\,y\,\)の変域（値域）が\(\,0≦y≦6\,\)となっているのは、④だけです。

答え　\(\,\underline{　④　}\,\)

ここでの値域は直線なので両端を考えれば良かったのですが、
途中で増加、減少に変化がある関数でも、

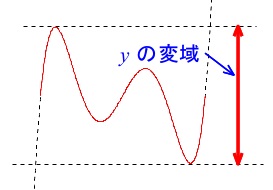
\(\,y\,\)の変域（値域）は、「定義域内での最小値と最大値の範囲」ですので覚えておきましょう。

次は\(\,1\,\)次関数の求め方です。

関数の決定問題はそれぞれの関数での最も大切な基礎になりますので、
しっかりポイントをおさえておきましょう。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

これが不十分だと入試の数学は関数を捨てることになります。

⇒　比例と反比例の関数の比例定数を決める問題の解き方と座標の求め方

比例定数を求める問題は、比例、反比例の関数決定問題ですよ。

クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！

その悩み、『覚え太郎』が解決します！！！