比例の関数と反比例の関数を求めるための比例定数を決める問題の解き方です。
基本的なところですが関数を攻略する大切なポイントになります。
比例定数とは？という注意点もあるので確認しておきましょう。
ここでは比例と反比例の二つの関数を求めることになりますが、
入試まで方法は同じでかまいません。
関数を求める問題の解き方はすべての関数で同じです。
ここは簡単なのでちゃちゃっと進めますが、忘れてはいけないことがありますので確認しておくと良いです。
比例を表す関数の形と比例定数
高校入試までは、出てくる関数は４つしかありません。
だから「関数を求めよ。」という問題の答えの形は４つしかないということです。
１年であつかうのは二つですがそのひとつが比例です。
比例関数の形はすべて
\(\large{\color{red}{y=ax}}\)
です。
これ以外の形になれば比例ではありません。
似た形に\(\,y=ax+b\,\)という一次関数がありますが比例ではありません。
（\(\,b\,\)を\(\,\color{red}{ y 切片}\,\)といいますが、\(\,\color{red}{b=0}\,\) のとき比例になります。）
つまり、「比例」と書いてあればすべて\(\,\color{red}{y=ax}\,\)となる、
と決めつけて良いのです。
関数では \(\,x,y\,\) は関係式に残るので
\(\color{red}{比例定数\,a\,を決めれば}\)
それで関数が決まります。
反比例を表す関数の形と比例定数
一方で反比例は関数の形が
\(\large{\color{red}{\displaystyle y=\frac{a}{x}}}\)
となる場合です。
\(xy=a\) も反比例ですが上の関数と同じです。
だから問題に「反比例」とあればすべて \(\color{red}{\displaystyle y=\frac{a}{x}}\) と決めつけて良いです。
この場合も \(\color{red}{a\,を決めれば}\)それで関数が決まります。
比例定数とは？比例定数の注意点
比例の関数
\(\hspace{4pt}y=\color{red}{a}\,x\,\)
反比例の関数
\(\hspace{4pt}\displaystyle y=\frac{\color{red}{a}}{x}\)
さらに\(\,y\,\)が\(\,x^2\,\)に比例する関数
\(\hspace{4pt}y=\color{red}{a}\,x^2\)
これらの\(\,\color{red}{a}\,\)はすべて比例定数と呼ばれますので注意しておきましょう。
ここでは比例と反比例だけ見ておけば良いですが、
比例の場合も反比例の場合も、
比例定数を決めれば関数が決まる。
ということですね。
比例と反比例の関数の比例定数の求め方と座標の求め方問題
いくつか問題を解いてみればすぐに求められるようになります。
注意してほしいのは問題で聞かれていることを答えていないときがある、ということです。
それと、途中の段階をやろうとしない人が多すぎます。
飛ばして良い段階は関数問題ではありません。
問題の中で説明します。
\(y\) は \(x\) に比例し，\(x=3\) のとき，\(y=24\) である。
\(y\) を \(x\) の式で表せ。
気がついてください。
問題に『 \(y\) は \(x\) に比例し』とあります。
この関数は \(\color{red}{y=ax}\) となっているということです。
これが \(x=3\) のとき \(y=24\) をみたす。
つまり \((\,3\,,\,24\,)\) を通るということです。
代入すれば良いだけですね。
\(\color{red}{y=ax}\) に \((\,3\,,\,24\,)\) を代入して、
\((24)=a\times (3)\) から \(24=3a\)
\(∴ a=8\)
よって求める関数は、\(\underline{ y=8x }\)
問題に比例とあれば \(y=ax\) とおく、それだけです。
求めるのは比例定数の \(a=8\) ではありませんよ。
\(y\) は \(x\) に反比例し，点 \((\,-2\,,\,-11\,)\) を通るとき，
\(y\) を \(x\) の式で表せ。
これは問題に『 \(y\) は \(x\) に反比例し』とあるので、
\(\displaystyle \color{red}{y=\frac{a}{x}}\)
とおいて比例定数を求めます。
点 \((\,-2\,,\,-11\,)\) を通るので代入すると
\(\begin{eqnarray}
\displaystyle (-11)&=&\frac{a}{(-2)}\\
22&=&a
\end{eqnarray}\)
これが答えではありません。
答え \(\displaystyle \underline{\underline{ y=\frac{22}{x} }}\)
比例 \(y=-4x\) で， \(x\) の変域が \(－1\,≦\,x\,≦\,1\) のときの \(y\) の変域を求めよ。
変域について説明していなかったので問題に入れておきました。
関数において、
\(x\) の値の取る範囲を \(x\) の変域
\(y\) の値の取る範囲を \(y\) の変域
といいます。
教科書だと「変数の取る値の範囲を変域」と書いてあるかもしれません。
\(x\) の変域とは左右の範囲
\(y\) の変域とは上下の範囲
のことです。
これが高校生になってわからなくしている原因のひとつです。
確かに、変数の取り得る範囲を変域といいますが、
\(\color{red}{y \,の変域は『値域』}\)
ということが多いので、高校生は覚えておくと良いです。
『値域を求めよ。』は『 \(y\) の変域を求めよ。』ということです。
今は『変域』という言葉だけで済ませておきましょう。
ポイントはそこではないので今は無視しておいてください。笑
この問題のポイントは、変域を求めるとき、グラフを書かない人がいるということです。
問題に比例と書いてあるということは関数の問題です。
関数の問題をグラフなしで考えるのは、10年はやいですね。
\(y=-4x\) で， \(x\) の変域が \(－1\,≦\,x\,≦\,1\)
\(x=-1\) のとき \(y=-4\times (-1)=4\)
\(x=1\) のとき \(y=-4\times (1)=-4\)
だから、\(y\) の変域は \(4\,≦\,y\,≦\,-4\)
なんてことを絶対にしないようにしてください。
数値だけで考えようとしているからだけではありません。
そもそも \(4\,≦\,y\,≦\,-4\) なんて範囲はあり得ないです。
ん？おかしいことに気がついていない？
\(4\) と \(-4\) はどっちが大きいのですか？
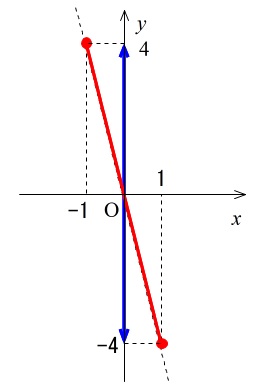
これから先ずっと、変域を考えるときはグラフで考えるようにしてください。
はっきり言ってグラフをいちいち書くのは面倒です。
ここでグラフを挿入するのもめんどうです。笑
しかし、そのちょっとした手間を惜しまなければ簡単でミスが確実に減ります。
特に３年になってミスする人はグラフを書いていない人ですよ。
答えは \(\underline{ \,-4\,≦\,y\,≦\,4\, }\)
反比例 \(\displaystyle y=-\frac{10}{x}\) で，\(y=2\) のときの \(x\) の値を求めよ。
これは関数が定まっているので代入問題と同じです。
\(\displaystyle y=-\frac{10}{x}\) で\(\,y\,\) が \(2\) になるときの \(x\) は？
ということですが、
\(\,x\) をひとつ決めれば \(y\) もひとつだけ決まるものを関数といいます。
ただし、\(y\) が決まれば \(x\) がひとつとは限りません。
しかし、この場合はひとつです。
\(\displaystyle y=-\frac{10}{x}\) に \(y=2\) を代入すると、
\(\begin{eqnarray}
\displaystyle (2)&=&-\frac{10}{x}\\
2x&=&-10\\
x&=&\underline{ -5 }
\end{eqnarray}\)
方程式では分母をなくすように、先に処理すればすべて同じですよ。
\(x\) がわかっているときの \(y\) の値を求めるときも,
同じように代入すれば良いだけです。
上の４題はひとつの段階だけで答えが出るので間違えることは少ないです。
もちろんグラフを書いて考えるというのは段階に入れていません。
鉛筆が止まるのは次のような問題です。
なれている人に取ってはなんてことはないのですが、手順を覚えていない人はこの程度で考え込んでしまいます。
考え込んでも答えが出るわけではないですよ。
\(y\) は \(x\) に比例していて \( x=-3\) のとき \(y=12\) です。
\(x=3\) のとき \(y\) の値を求めなさい。
この問題は上の問題(1)と(4)を合わせたような問題です。
やることは同じなのですが、やらない人が多いです。
『\(y\) は \(x\) に比例し』
とあるので、この関数は \(y=ax\) とおくことができます。
これをやらないんです。
関数の形は決まっていますのでまずは比例定数を決めに行きましょう。
\(y=ax\) は \( x=-3\) のとき \(y=12\) なので、
\((12)=a\times (-3)\) と代入して \(a=-4\)
よってこの関数は \(y=-4x\) です。
\(y=-4x\) で \(x=3\) のとき
\(y=-4\times (3)=-12\)
（答え）\(\underline{ y=-12 }\)
この関数を求めることはできるはずですが、求めようとしないんですよね。
なんか他に簡単な方法があるのか考えているのでしょうか？
確かに比例では比例定数が一定だから \(x\) が \(0\) でなければ
\(\displaystyle a=\frac{y}{x}\)
なので
\(\displaystyle a=\frac{12}{-3}=-4\)
とすることもできますが、\(x\) が \(0\) じゃないときとか、考える方がめんどくさいでしょう。
関数ではまずは関数を求める（定める）ことを基本にしておきましょう。
後はグラフを書いて考えれば簡単なものばかりですよ。
比例でも反比例でも、他の関数でも同じです。
次は比例関数と座標上の面積の問題をみておきましょう。
⇒ 比例と反比例のグラフから三角形,四角形の面積を求める問題の解き方
比例のグラフと反比例のグラフと面積の問題は、
図形の問題と考えても良いくらい簡単です。
図形に置きかえて考える前に、座標の基本は復習しておきましょう。
関数と図形が融合された応用問題は入試では多いですが、
それぞれの基本が抜け落ちていると対応できないです。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
