平行線の同位角と錯角を利用して角度を求める問題の解き方

平行線の同位角と錯角を利用して角度を求める問題の解き方の解説です。
分かり易いところなので得点しやすいですが、理解していないと大きな差となります。
落とせないところなのでいくつかの出題パターンを確認しておきましょう。
1つだけ注意するとすれば、同位角と錯角は平行線の場合だけ等しくなることです。

対頂角と同位角と錯角の確認

対頂角とは2つの直線が交わるとき交点をはさむ対角のことをいいます。
対頂角はいつも等しくなります。

同位角と錯角は2本の直線と交わる直線があるときの、
同じ方位にある角度とその対頂角のことをいいます。
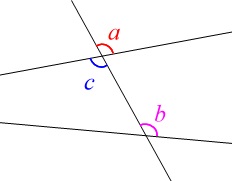図でいうと

　\(\,\color{red}{a}\,\)と\(\,\color{magenta}{b}\,\)は同位角
　\(\,\color{magenta}{b}\,\)と\(\,\color{blue}{c}\,\)は錯角

の関係になります。

注意しておきたいのは、

　同位角と錯角はいつも等しいわけではない

ということです。
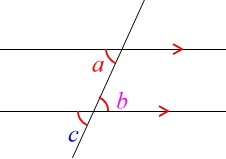図のように、

　\(\,2\,\)本の直線が平行なとき同位角と錯角は等しくなります。

逆に、同位角と錯角が等しいときは\(\,2\,\)本の直線は平行であると言えます。

つまり、
2本、またはそれ以上の平行線がある場合の特別な関係なので、

　平行線があれば同位角と錯角は等しい

という関係を使うと考えて良いです。
※
\(\,1\,\)次関数では平行といえば、傾きが等しい場合です。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い　

平行線が作る角度を求める問題の解き方

平行線でできる角度が与えられるときの問題の解き方を2つお伝えします。

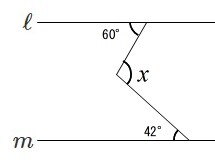
平行線を補助する場合

内角の和や外角を利用する方法を後でお伝えしますが、
平行線を補助線として利用する方法を覚えましょう。

定期テストなどで出てくる平行線の角度はほとんどがこれで求まります。

簡単です。
折れ曲がった頂点に平行線を引いて、同位角、錯角が等しいことを利用するだけです。
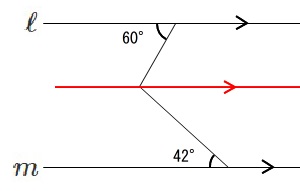すると錯角が等しいので、
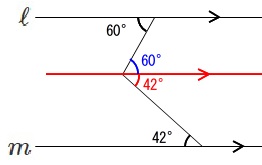これから求める角\(\,x\,\)は

　\(\begin{eqnarray}
x&=&60^{\circ}+42^{\circ}\\
&=&\underline{　102^{\circ}　}
\end{eqnarray}\)

折れ曲がるところがいくつになっても平行線を引く方法は使えます。

線分の延長を補助する場合

線分を延長します。
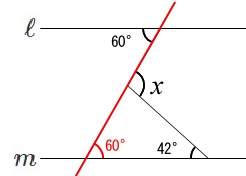または
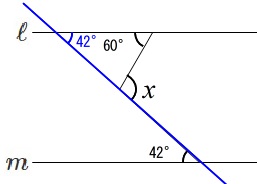どちらも同じですが、

　三角形の内角の和が180°
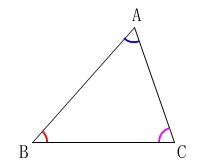　\(\,\mathrm{∠\color{blue}{A}+∠\color{red}{B}+∠\color{magenta}{C}=180^{\circ}}\,\)

または
　三角形の1つの外角は他の2つの内角の和
　
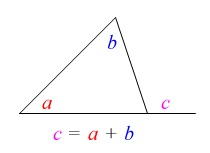
を使いますが、このことは多角形の内角、外角の説明でも詳しくします。

内角の和が\(\,180°\,\)なので\(\,x\,\)の反対側の角度\(\,\color{blue}{y}\,\)は
　
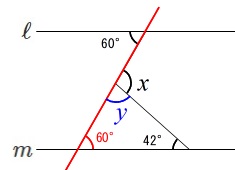
　\(\begin{eqnarray}
60^{\circ}+42^{\circ}+\color{blue}{y}&=&180^{\circ}\\
102^{\circ}+\color{blue}{y}&=&180^{\circ}\\
\color{blue}{y}&=&180^{\circ}-102^{\circ}\\
&=&78^{\circ}
\end{eqnarray}\)

よって

　\(\begin{eqnarray}
x&=&180^{\circ}-78^{\circ}\\
&=&\underline{　102^{\circ}　}
\end{eqnarray}\)

三角形の内角の和から求めると二度同じ計算をしているのが分かるでしょう。
　
　\(\begin{eqnarray}
x&=&60^{\circ}+42^{\circ}\\
&=&\underline{　102^{\circ}　}
\end{eqnarray}\)

これはよく使うので覚えておきましょう。

補助線を利用する場合は、平行線か垂線がほとんどですが、角度の問題では延長線も効果的な場合も多いです。

平行線の角度のいろいろな問題パターンと求め方

平行線の同位角や錯角を利用する問題をいくつかやっておきましょう。

\(\color{black}{\fbox{\(\,ex\,1\,\)}}\)
\(\,\ell \,/\!/ \,m\,\)のとき\(\,x\,\)を求めなさい。
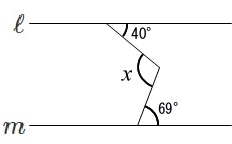平行線の同位角と錯角を使いまくりましょう。

折れ曲がったところに平行線を引きます。
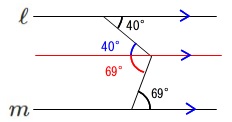平行線の錯角は等しいので、

　\(\begin{eqnarray}
x&=&\color{blue}{40^{\circ}}+\color{red}{69^{\circ}}\\
&=&\underline{　109^{\circ}　}
\end{eqnarray}\)

\(\color{black}{\fbox{\(\,ex\,2\,\)}}\)
\(\,\ell \,/\!/ \,m\,\)のとき\(\,x\,\)を求めなさい。
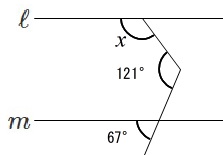平行線を引くまでは同じです。

角度を求める問題ではすぐに答えに直結する場合は少ないですが、
次から次へと分かる角度を書いていけば見えてきます。
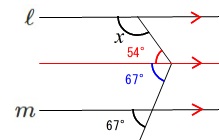平行線の同位角が等しいことから

　　\(121^{\circ}=\color{blue}{67^{\circ}}+\color{red}{54^{\circ}}\)

と分けることができます。

ここからは2つの見方がありますが、やっていることはどちらも同じです。
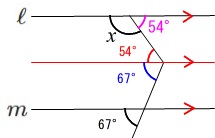錯角の\(\,\color{magenta}{54^{\circ}}\,\)を書き込めば、直線の角度\(\,180°\,\)から

　\(\begin{eqnarray}
x+\color{magenta}{54^{\circ}}&=&180^{\circ}\\
x&=&180^{\circ}-\color{magenta}{54^{\circ}}\\
&=&\underline{　126^{\circ}　}
\end{eqnarray}\)

もう一つは平行四辺形でも言えることですが、
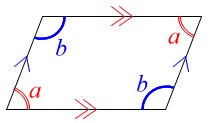\(\,2\,\)本の平行線で作る同じ側の2つの角の和が\(\,180°\,\)なることから

　\(\color{red}{a}+\color{blue}{b}=180^{\circ}\)

よって

　\(\begin{eqnarray}
x+\color{red}{54^{\circ}}&=&180^{\circ}\\
x&=&180^{\circ}-\color{red}{54^{\circ}}\\
&=&\underline{　126^{\circ}　}
\end{eqnarray}\)

\(\color{black}{\fbox{\(\,ex\,3\,\)}}\)
\(\,\ell \,/\!/ \,m\,\)のとき\(\,x\,\)を求めなさい。
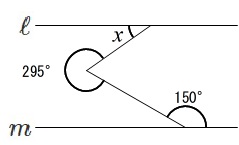平行線を引きますが、補角を見た方が計算が楽です。
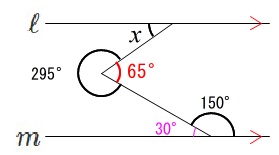\(\,150^{\circ}\,\)の補角は\(\,\color{magenta}{30^{\circ}}\,\)で、

　\(360°-295°=\color{red}{65°}\)

なので錯角が等しいことから

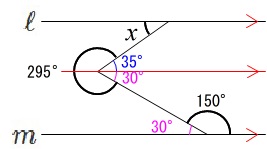
　\(\begin{eqnarray}
x&=&65°-30°\\
&=&\underline{　35^{\circ}　}
\end{eqnarray}\)

\(\color{black}{\fbox{\(\,ex\,4\,\)}}\)
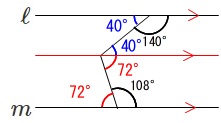
\(\,\ell \,/\!/ \,m\,\)のとき\(\,x\,\)を求めなさい。
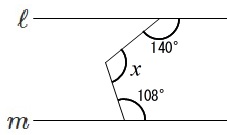これも補角の方がはやいですね。
角\(\,x\,\)は補角の和になります。

　\(\begin{eqnarray}
x&=&\color{blue}{40^{\circ}}+\color{red}{72^{\circ}}\\
&=&\underline{　112^{\circ}　}
\end{eqnarray}\)

\(\color{black}{\fbox{\(\,ex\,5\,\)}}\)
\(\,\ell \,/\!/ \,m\,\)、\(\,\mathrm{△ABC}\,\)が正三角形のとき\(\,x\,\)を求めなさい。
これも平行線を加えますが、\(\,\mathrm{△ABC}\,\)が正三角形という条件を見逃すと求めることはできません。
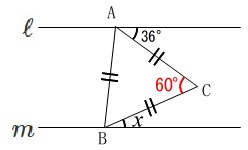頂点\(\,\mathrm{C}\,\)を通る平行線を加えると
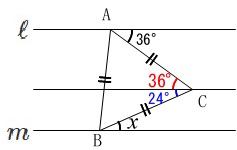平行線の錯角は等しいので、

　\(x=\underline{　24^{\circ}　}\)

\(\color{black}{\fbox{\(\,ex\,6\,\)}}\)
\(\,\ell \,/\!/ \,m\,\)のとき\(\,x\,\)を求めなさい。

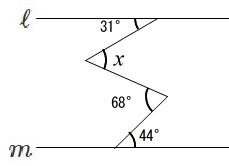平行線を増やせば良いだけです。
錯角を順に書き込んで行くと、
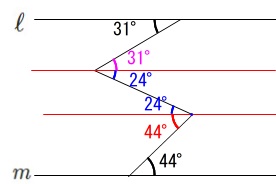求める角度\(\,x\,\)は

　\(\begin{eqnarray}
x&=&\color{blue}{24^{\circ}}+\color{magenta}{31^{\circ}}\\
&=&\underline{　55^{\circ}　}
\end{eqnarray}\)

\(\color{black}{\fbox{\(\,ex\,7\,\)}}\)
\(\,\ell \,/\!/ \,m\,\)のとき\(\,x\,\)を求めなさい。
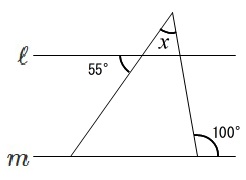この問題は角に平行線を引くことはできますが、
三角形の内角の和を利用した方がはやいです。
平行線の錯角が等しいことを利用するのは同じです。
補角の\(\,\color{red}{80°}\,\)と合わせると、

　\(\begin{eqnarray}
x+\color{blue}{55^{\circ}}+\color{red}{80^{\circ}}&=&180^{\circ}\\
x+135^{\circ}&=&180^{\circ}\\
x&=&180^{\circ}-135^{\circ}\\
&=&\underline{　45^{\circ}　}
\end{eqnarray}\)

または
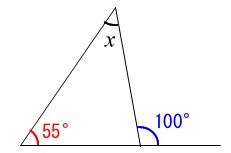三角形の1つの外角が\(\,100°\,\)なので

　\(\begin{eqnarray}
x+\color{red}{55^{\circ}}&=&\color{blue}{100^{\circ}}\\
x&=&\color{blue}{100^{\circ}}-\color{red}{55^{\circ}}\\
&=&\underline{　45^{\circ}　}
\end{eqnarray}\)

でも良いです。
どちらかというとは外角を利用した方がはやいですね。

多角形の内角の和を求める公式などを別に解説しますが、
多角形でも外角は便利に使えますよ。

⇒　全国の公立高校入試 数学過去問の解答解説

平行線や外角の利用は全国の公立入試でもよく取り上げられています。

⇒　多角形の内角の和の公式と外角の和を利用した角度の求め方

公式もありますが、考え方を身につけておくと図形問題に強くなれます。