多角形の内角の和の公式と外角の和を利用した角度の求め方

多角形の内角の和は公式がありますので求め方と示す意味を見ておきましょう。
角度を求める問題はいろいろな形で入試でも多く取り上げられますが、
内角の和を使うより外角の和を利用した方が楽な計算になることがありますので、その理由と角度の求め方の練習をしておきましょう。

多角形の内角の和の公式と意味

多角形の基本の形は三角形です。

　四角形は三角形が2つ
　五角形は三角形が3つ
　六角形は三角形が4つ
　・・・

と増えていくだけです。

なので多角形の内角の和は三角形の数に関係しています。

　三角形の内角の和は\(\,180°\,\)

これは忘れたら角度は求まりません。

多角形の内角の和の公式を表しておきます。

　三角形は\(\,180°\,\)が\(\,1\,\)個分
　四角形は\(\,180°\,\)が\(\,2\,\)個分
　五角形は\(\,180°\,\)が\(\,3\,\)個分
　・・・
　\(\,n\,\)角形は\(\,180°\,\)が\(\,(\,n-2\,)\,\)個分

よって\(\,n\,\)角形の内角の和は

　\(\large{\color{red}{\fbox{\(　\color{red}{180\,(\,n-2\,)　度　}\)}}}\)

となります。

多角形の外角の和

多角形の外角の和は理屈抜きに覚えておきましょう。

正多角形でも普通の多角形でも外角の和はいつも\(\,360°\,\)です。

多角形の外角とは多角形の頂点の外側の角度のことです。
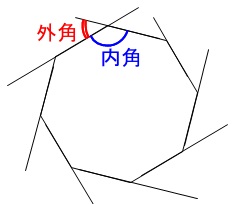多角形の内部の一つひとつの角を内角、内角の補角を外角といいます。
外角は2つありますが、

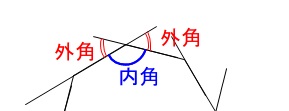
外角の和を考えるときは1つの頂点では1つの外角だけを見ます。

外角は内角の補角になっているので、

　\(\,\color{blue}{内角}+\color{red}{外角}=180°\,\)

\(\,n\,\)角形の場合、頂点は\(\,n\,\)個あるので、
内角と外角の和の合計は

　\(\,\color{magenta}{180\times n}　(度)\,\)

内角の和は\(\,\color{blue}{180\,(\,n-2\,)}　(度)\,\)なので

　\(\begin{eqnarray}
　(\color{red}{外角の和})&=&\color{magenta}{180\,n}-\color{blue}{180\,(\,n-2\,)}\\
&=&180\,n-180\,n+360\\
&=&\color{red}{360　(度)}
\end{eqnarray}\)

と、いつも外角の和は\(\,360°\,\)になります。

多角形の中で問われる角度の求め方練習問題

角度を求める問題は分かるところを次から次へと書き込めば、
合同や相似も利用することもありますが必ず出てきます。

ここでは合同や相似は使わないで、基本的な角度を求める問題を見ておきましょう。

正九角形は1つの頂点から対角線を引くことによって7つの三角形に分けることができます。
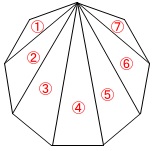よって内角の和は

　\(\hspace{10pt}180^{\circ}\times 7\\
=\underline{　1260^{\circ}　}\,\)

多角形の内角の和の公式

　\(\color{red}{180^{\circ}\times (n-2)}\)

を覚えているのなら、当然ですが正多角形にも使えるので

　\(\hspace{10pt}180^{\circ}\times (9-2)\\
=1260^{\circ}\)

でも、もちろん良いです。

または外角の和がいつも\(\,360°\,\)であることから、
正九角形の外角の1つは

　\(\hspace{10pt}360^{\circ}\div 9\\
=40^{\circ}\)

なので1つの内角は

　\(\hspace{10pt}180^{\circ}-40^{\circ}\\
=140^{\circ}\)
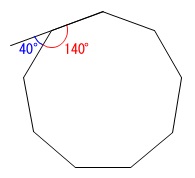頂点は\(\,9\,\)個あるので

　\(\hspace{10pt}140^{\circ}\times 9\\
=1260^{\circ}\,\)

外角から探れば、\(\,360°\,\)以上の角度は出ないので割と小さな数値で計算を進めることができます。

公式を使って正十二角形の内角の和を求めると

　\(\hspace{10pt}180^{\circ}\times (12-2)\\
=1800^{\circ}\)

これは内角\(\,12\,\)個分なので1つの内角は

　\(\hspace{10pt}1800^{\circ}\div 12\\
\displaystyle =\frac{1800^{\circ}}{12}\\
\displaystyle =\underline{　150^{\circ}　}\)

または外角の和を利用すると、

　正十二角形の外角の和が\(\,360°\,\)

なので、1つの外角は

　\(\hspace{10pt}360^{\circ}\div 12\\
\displaystyle =\frac{360^{\circ}}{12}\\
=\color{red}{30^{\circ}}\)

よって正十二角形の1つの内角は

　\(\hspace{10pt}180^{\circ}-\color{red}{30^{\circ}}\\
=\underline{　150^{\circ}　}\)

外角の和を利用する方があつかう数値は確実に小さいです。

内角の和からいきなり外角は出せません。

1つの外角を求めるので先ずは正多角形の頂点がいくつあるかを求めましょう。

内角の和の公式から

　\(\begin{eqnarray}\displaystyle
180\,(n-2\,)&=&2340\\
n-2&=&\frac{2340}{180}\\
n-2&=&13\\
n&=&13+2\\
n&=&15
\end{eqnarray}\)

正十五角形だと分かるので1つの外角は

　\(360^{\circ}\div 15=\underline{　24^{\circ}　}\)

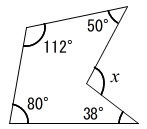
補助（延長）線を引いて内角の和などを利用して求まります。

こういう形をした多角形を凹多角形といいますが、気にしなくて良いです。笑

四角形や三角形に分けて、分かる角度を書き込んで行けば簡単に求まります。

赤線の補助線を入れると四角形の内角の和から

　\(\hspace{10pt}360-(50+112+80)\\
=360-242\\
=\color{red}{118}　(度)\)
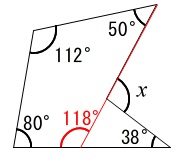この\(\,\color{red}{118°}\,\)は右下の三角形の1つの外角なので\(\,∠x\,\)の補角は

　\(\hspace{10pt}118^{\circ}-38^{\circ}\\
=\color{blue}{80^{\circ}}\)
よって
　
　\(\begin{eqnarray}
x&=&180^{\circ}-80^{\circ}\\
&=&\underline{　100^{\circ}　}
\end{eqnarray}\)

順番に分かることを出して行けば答えは出ますよ。

違う方法もあります。
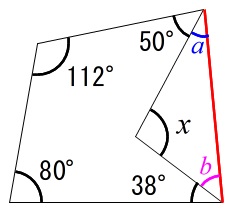赤線を引いて四角形を作ると内角の和から

　\(\begin{eqnarray}
50+112+80+38+\color{blue}{a}+\color{magenta}{b}&=&360\\
280+\color{blue}{a}+\color{magenta}{b}&=&360\\
\color{blue}{a}+\color{magenta}{b}&=&360-280\\
\color{blue}{a}+\color{magenta}{b}&=&\color{red}{80}　(度)
\end{eqnarray}\)

三角形の内角の和から

　\(\begin{eqnarray}
x+\color{blue}{a}+\color{magenta}{b}&=&180^{\circ}\\
x+\color{red}{80^{\circ}}&=&180^{\circ}\\
x&=&180^{\circ}-\color{red}{80^{\circ}}\\
&=&\underline{　100^{\circ}　}
\end{eqnarray}\)

と具体的には\(\,a,b\,\)は求まっていませんが、\(\,∠x\,\)は求めることができます。

角度を求める問題はいろいろなタイプがありますが、
どれも使う方法は基本的なことばかりです。

⇒　中学２年 平行と合同と証明の書き方ポイントまとめ

合同や相似や円周角の定理を使うようになるとまた違った角度の求め方が使えますが、
分かる部分の角度を求め、次に分かる角度を求め、と繰り返すことは同じですよ。

⇒　平行線の同位角と錯角を利用して角度を求める問題の解き方

平行線の同位角と錯角を利用する方法は「相似」でも利用するので忘れないようにしましょう。

⇒　高校入試対策 中学数学単元別の要点とまとめ

入試に必要なことは、すべての範囲の基本を確実に身につけておくことです。

⇒　中学数学最短攻略『覚え太郎』

他の教科に時間を回し、短時間で数学の対策を済ませたい人にはおすすめします。
いい加減に取り組んだ人は伸びない、それには理由があるのです。