2019年京都府公立高校入試【中期】試験数学問題の解説(後半)

2019年(平成31年度)京都府で行われた公立高校入試中期試験の数学問題の解説後半部分です。
第4問は制動距離に関する2次関数、第5問は折り返した図形の性質、第6問は座標と規則性の融合問題です。
教科書に添った問題ですが、少しひねってありますので問題に取り組むときの方針を持っていないと得点しにくいかもしれません。

問題は京都府で公開してくれています。

⇒　2019京都府中期数学問題

\(\,\large{4}\,\)は「制動距離」についての関数問題です。

4.制動距離の関数問題

制動距離については教科書にありますが、\(\,y\,\)が\(\,x^2\,\)乗に比例する関数のことです。
（この問題では書いてくれています。）
ただし、ここでは単に比例定数を求めるだけではありません。

比例定数を先に決めておきましょう。

　「制動距離は、速さの\(\,2\,\)乗に比例する」

と問題に書いてあるように速さ\(\,x\,\)、制動距離\(\,y\,\)とすると

　\(y=\color{red}{a}x^2\)

となります。

この\(\,\color{red}{a}\,\)は比例定数です。

　比例　\(\,y=\color{red}{a}x\,\)
も
　反比例　\(\,\displaystyle y=\frac{\color{red}{a}}{x}\)
も\(\,\color{red}{a}\,\)は比例定数ですよ。

違うのは\(\,1\,\)次関数　\(y=\color{blue}{a}x+b\)　の\(\,\color{blue}{a}\,\)を「傾き」と呼ぶことです。

問題の最初、(1)の問の前に
　「秒速\(\,2\,\mathrm{m}\,\)で走るときの制動距離は\(\,0.5\,\mathrm{m}\,\)」
と書いてあります。

　\(y=\color{red}{a}x^2\)

に代入して比例定数を決めます。

(1)
　\(\begin{eqnarray}\displaystyle
0.5&=&\color{red}{a}\times (2)^2\\
\frac{1}{2}&=&4a\\
\color{red}{a}&=&\frac{1}{8}
\end{eqnarray}\)

よって、

　\(\displaystyle \underline{　y=\frac{1}{8}x^2　}\)

関数で大切なのは\(\,x\,\)が何で、\(\,y\,\)が何かをしっかり意識しながら考えることです。

(1)には続きがあります。

　「\(\,x\,\)が\(\,5\,\)から\(\,7\,\)まで変化するとき、\(\,y\,\)の増加量は\(\,x\,\)の増加量の何倍か」

これは「変化の割合」のことですね。

関数は\(\displaystyle \,y=\frac{1}{8}x^2\,\)です。

　\(x=5\)　のとき　\(\displaystyle y=\frac{25}{8}\)

　\(x=7\)　のとき　\(\displaystyle y=\frac{49}{8}\)

このとき

　\(\,(x\,の増加量)=7-5=\color{red}{2}\,\)

\(\,\begin{eqnarray}
　(y\,の増加量)&=&\displaystyle \frac{49}{8}-\frac{25}{8}\\
&=&\frac{49-25}{8}\\
&=&\frac{24}{8}\\
&=&\color{blue}{3}
\end{eqnarray}\)

よって\(\,y\,\)の増加量は\(\,x\,\)の増加量の

　\(\displaystyle \underline{　\frac{3}{2}　}　(倍)\)

(2)
速さを\(\,x\,\)として線分図を書けば簡単に方程式が立ちます。

速さ\(\,x\,\)で\(\,1.5\,\)秒間で進む距離は\(\,\color{red}{1.5\,x}\,\)、
ブレーキをかけてから停止するまでの距離は\(\displaystyle \,\color{blue}{\frac{1}{8}\,x^2}\,\)
これらの距離を合わせると\(\,\color{magenta}{13.5}\,\)なので

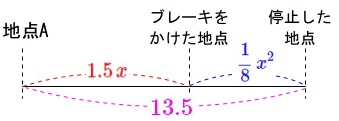
　\(\displaystyle \,\color{red}{1.5x}+\color{blue}{\frac{1}{8}x^2}=\color{magenta}{13.5}\,\)

これを解くと

　\(\begin{eqnarray}\displaystyle
1.5x+\frac{1}{8}x^2&=&13.5\\
1.5x\times 8+x^2&=&13.5\times 8\\
12x+x^2&=&108\\
x^2+12x-108&=&0\\
(x-6)(x+18)&=&0\\
x&=&6\,,\,-18
\end{eqnarray}\)

速さなので

　\(\,x=6\)

(答え)　\(\,秒速　\underline{　6　}　\mathrm{(m)}\,\)

5.図形の折り返しと合同と相似

長方形を折り返す問題です。

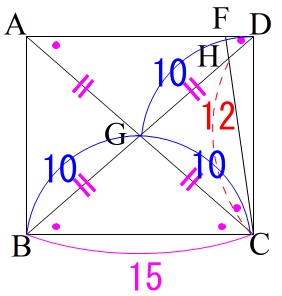
\(\,Ⅰ図\,\)と\(\,Ⅱ図\,\)がありますので条件を図示していきます。

\(\,Ⅰ図\,\)は長方形\(\,\mathrm{ABCD}\,\)を対角線\(\,\mathrm{AC}\,\)で折り返した図です。
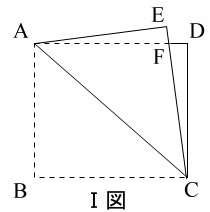\(\,Ⅱ図\,\)は折り返した部分の跡を一部残し、元に戻した図で、
　\(\,\mathrm{CH=\color{red}{12}}\,\)　,　\(\,\mathrm{GH=\color{red}{8}}\,\)　です。

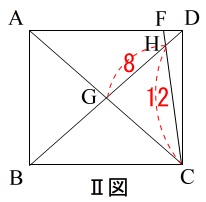
折り返した図形には等しい辺や角があります。

折り返された辺は等しいので、

　\(\,\mathrm{AB=AE}\,\)
　\(\,\mathrm{BC=CE}\,\)

折り返された角度は等しいので

　\(\,\mathrm{∠ACB=∠ACE}\,\)
　\(\,\mathrm{∠BAC=∠EAC}\,\)
　\(\,\mathrm{∠ABC=∠AEC=90°}\,\)

また、\(\,\mathrm{ABCD}\,\)は長方形（平行四辺形で対角線が等しい）であることを合わせて図示すると

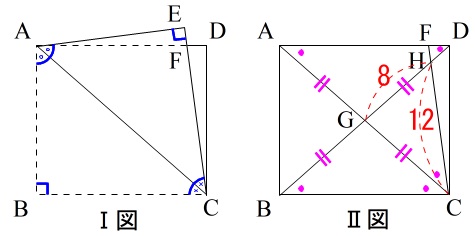
(1)
\(\,\mathrm{∠BCG}\,\)と大きさが等しい角は\(\,\color{magenta}{●}\,\)で
　
　\(\begin{eqnarray}
\mathrm{∠BCG}&=&\mathrm{∠GCH}\\
&=&\mathrm{∠GBC}\\
&=&\mathrm{∠CAD}\\
&=&\mathrm{∠HDF}
\end{eqnarray}\)

この中で選択肢に一致するのは、

　\(\,\mathrm{∠CBG}\,\)　,　\(\,\mathrm{∠FDH}\,\)　,　\(\,\mathrm{∠GCH}\,\)

答え　\(\,\underline{　(ア)\,,\,(オ)\,,\,(カ)　}\,\)

(2)
\(\,\mathrm{BG}\,\)の長さです。

これは(1)が言えれば簡単で、

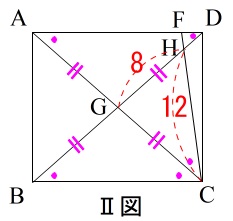
　\(\,\mathrm{△HCG}\,\)　∽　\(\,\mathrm{△HBC}\,\)
なので、

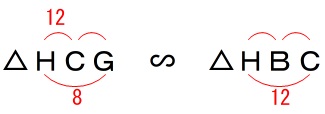
　\(\begin{eqnarray}\displaystyle
12:\mathrm{HB}&=&8:12\\
8\times \mathrm{HB}&=&12\times 12\\
\mathrm{HB}&=&\frac{12\times 12}{8}\\
&=&18
\end{eqnarray}\)

よって

　\(\begin{eqnarray}
\mathrm{BG}&=&\mathrm{HB-GH}\\
&=&18-8\\
&=&\underline{　10　}　(\mathrm{cm})
\end{eqnarray}\)

(3)
\(\,\mathrm{△DFH}\,\)の面積を求めます。

これも長方形から二等辺三角形が見つかっているので簡単ですが、
説明はめんどうです。笑
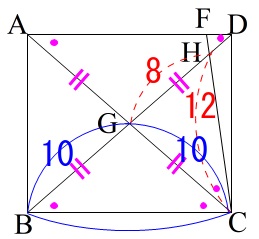再び相似を利用すると、
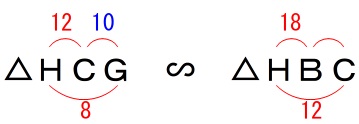相似比は\(\,2:3\,\)なので

　\(\begin{eqnarray}
2:3&=&\mathrm{CG:\color{magenta}{BC}}\\
2\times \mathrm{\color{magenta}{BC}}&=&3\times \mathrm{CG}\\
&=&3\times 10\\
\mathrm{\color{magenta}{BC}}&=&\frac{3\times 10}{2}\\
&=&\color{magenta}{15}
\end{eqnarray}\)

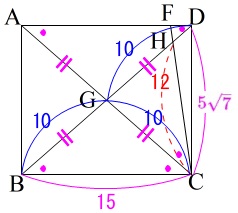
三平方の定理から

　\(\begin{eqnarray}
\mathrm{BC^2+DC^2}&=&\mathrm{BD^2}\\
15^2+\mathrm{DC^2}&=&20^2\\
\mathrm{DC^2}&=&20^2-15^2\\
&=&400-225\\
&=&175
\end{eqnarray}\)

\(\,\mathrm{DC}\,＞\,0\,\)なので

　\(\mathrm{DC}=\color{magenta}{5\sqrt{7}}\)

長方形の面積は

　\(5\sqrt{7}\times 15=\color{red}{75\sqrt{7}}\)

もう一度相似比に着目します。

　\(\,\mathrm{△DHF}\,\)　∽　\(\,\mathrm{△BHC}\,\)

で相似比は\(\,\color{red}{2}:\color{red}{18}\,\)です。
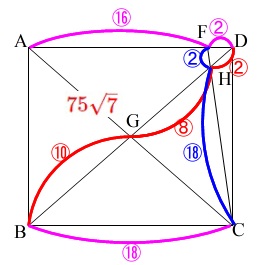ここからは長方形の面積\(\,\color{red}{75\sqrt{7}}\,\)を圧縮していけば出ます。

\(\,\mathrm{△ADC}\,\)は長方形の半分なので

　\(\displaystyle \mathrm{△ADC}=\frac{1}{2}\times \color{red}{75\sqrt{7}}\)

　\(\,\mathrm{AF:FD=16:2}\,\)
つまり
　\(\,\mathrm{AD:FD=\color{magenta}{18}:\color{magenta}{2}}\,\)
なので

　\(\begin{eqnarray}\displaystyle
\mathrm{△FDC}&=&\frac{\color{magenta}{2}}{\color{magenta}{18}}\times \mathrm{△ADC}\\
&=&\frac{1}{9}\times \mathrm{△ADC}\\
&=&\frac{1}{9}\times \frac{1}{2}\times \color{red}{75\sqrt{7}}
\end{eqnarray}\)

さらに

　\(\,\mathrm{FH:HC=\color{blue}{2}:\color{blue}{18}}\,\)
つまり
　\(\,\mathrm{FH:FC=\color{blue}{2}:\color{blue}{20}}\,\)

なので

　\(\begin{eqnarray}\displaystyle
\mathrm{△DFH}&=&\frac{\color{blue}{2}}{\color{blue}{20}}\times \mathrm{△FDC}\\
&=&\frac{1}{10}\times \mathrm{△FDC}\\
&=&\frac{1}{10}\times \frac{1}{9}\times \frac{1}{2}\times \color{red}{75\sqrt{7}}\\
&=&\underline{　\frac{5\sqrt{7}}{12}　}　(\mathrm{cm^2})
\end{eqnarray}\)

面積の圧縮はあちこちの公立入試解説でしてありますので省略します。

⇒　全国の公立高校入試 数学過去問の解答解説

6.関数と自然数の座標（格子点）と規則性

座標\(\,x,y\,\)がともに整数の点を格子点と呼びます。
覚えなくて良いですがここの解説だけでも通じるように今だけ覚えておいて下さい。

問題の条件は、

　\(\,4\,\)点\(\,\mathrm{O,A,B,C}\,\)
　\(\,\mathrm{O}\,(\,0\,,\,0\,)\,\)
　\(\,\mathrm{A}\,(\,m\,,\,0\,)\,\)
　\(\,\mathrm{B}\,(\,m\,,\,3m\,)\,\)
　\(\,\mathrm{C}\,(\,0\,,\,3m\,)\,\)

でできる長方形\(\,\mathrm{OABC}\,\)があって、
周上の格子点と対角線\(\,\mathrm{AC}\,\)上の格子点は\(\,○\,\)、
内部の格子点は\(\,●\,\)で表すとします。

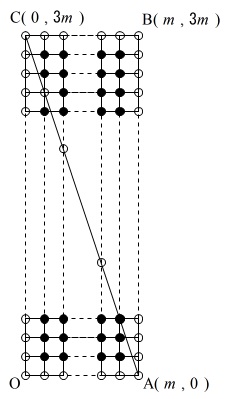
(1)は準備運動です。

実際に\(\,○\,\)と\(\,●\,\)を座標上に打って数えれば良いだけです。

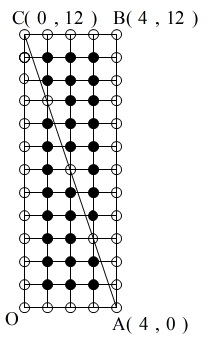
　\(\,○\,\)が\(\,\underline{　35　}\,\)個
　\(\,●\,\)が\(\,\underline{　30　}\,\)個

(2)
(1)では具体的に\(\,m\,\)が与えられていましたが、(2)では逆に\(\,m\,\)を求める問題です。

白い点\(\,○\,\)と、黒い点\(\,●\,\)の数を\(\,m\,\)を使って一般的に表せればすべて解決します。

白い点\(\,○\,\)が対角線上\(\,\mathrm{AC}\,\)にもあるのでその点だけ注意すれば、規則性としても容易な問題です。

対角線\(\,\mathrm{AC}\,\)は

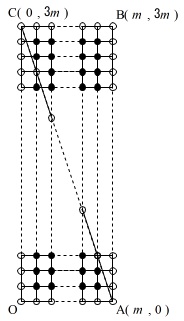
　\(\,\mathrm{A}\,(\,m\,,\,0\,)\,\)
　\(\,\mathrm{C}\,(\,0\,,\,3m\,)\,\)

を通るので、

　\(\begin{eqnarray}
y&=&-3x+3m\\
&=&-3(x-m)
\end{eqnarray}\)

白い点\(\,○\,\)となる\(\,\mathrm{A,C}\,\)以外の長方形内部の\(\,\mathrm{AC}\,\)上の格子点は、

　\(\,x\,\)が\(\,1\,\)から\(\,m-1\,\)までの整数の場合\(\,y\,\)も整数

になるので

　\(\,\color{red}{m-1}\,\)　個

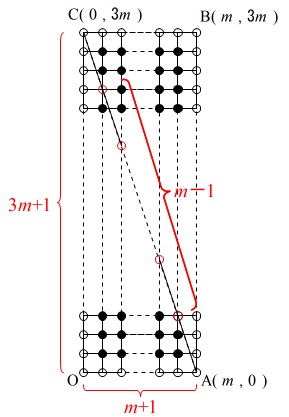
であることさえ見抜いてしまえばすぐ終わります。

横に並ぶ\(\,x\,\)軸上の格子点の数は

　\(\,0\,\)から\(\,m\,\)までの\(\,\color{blue}{m+1}\,\)個

これと同じ数の\(\,○\,\)が\(\,\mathrm{BC}\,\)上にあります。

原点\(\,\mathrm{O}\,\)から\(\,y\,\)軸上の点\(\,\mathrm{C}\,\)までの○の数は

　\(\,0\,\)から\(\,3m\,\)までの\(\,\color{magenta}{3m+1}\,\)個

これが\(\,\mathrm{AB}\,\)上にも同じ数あります。

これらを足すと

　\(\hspace{10pt}2(\color{blue}{m+1})+2(\color{magenta}{3m+1})+(\color{red}{m-1})\\
=2m+2+6m+2+m-1\\
=9m+3\)

となりますが、点\(\,\mathrm{O,A,B,C}\,\)上の\(\,4\,\)点は\(\,2\,\)回数えられているので、

\(\,○\,\)の数を\(\,m\,\)で表すと

　\(\hspace{10pt}(9m+3)\color{red}{-4}\\
=9m-1\)

これが\(\,458\,\)個のとき

　\(\begin{eqnarray}
9m-1&=&458\\
9m&=&458+1\\
&=&459\\
m&=&\underline{　51　}
\end{eqnarray}\)

また、
\(\,\mathrm{OA}\,\)上の格子点\(\,\color{red}{m+1}\,\)個は、
\(\,\mathrm{O}\,\)から\(\,\mathrm{C}\,\)までの\(\,\color{red}{3m+1}\,\)行あるので
\(\,○\,\)と\(\,●\,\)を合わせると

　\(\,\color{red}{(m+1)(3m+1)}\,\)個

あります。

\(\,m=51\,\)のときなので

　\(\hspace{10pt}(51+1)(3\times 51+1)\\
=52\times 154\\
=8008\)

白い点\(\,○\,\)の\(\,458\,\)を引けば黒い点\(\,●\,\)の数が出ます。

　\(8008-458=\underline{　7550　}\)

一般的に\(\,m\,\)を使って

全部の格子点が

　\(\,\color{red}{(m+1)(3m+1)}\,\)

白い点\(\,○\,\)が

　\(\,\color{blue}{9m-1}\,\)

黒い点\(\,●\,\)が

　\(\hspace{10pt}\color{red}{(m+1)(3m+1)}-(\color{blue}{9m-1})\)

と出しておけば(1)(2)を分けて考える必要はありません。
規則性に慣れていれば、(1)がなくても出せる関係式ですね。

格子点問題では格子点をグリグリと、できるだけ多く書き出すことで規則性が見やすくなりますよ。

\(\,2019\,\)年の京都府公立入試中期の数学は以上です。

⇒　2019年(平成31年度)京都府公立高校入試【中期】試験数学問題の解説

前半は\(\,\large{2}\,\)の資料の読み取りに少し時間が必要でしょう。
他の問題も手を動かさず、ながめているだけでは進まない問題が多いです。

⇒　京都府公立高校入試数学の過去問と解答解説

例年の問題で同じことが言えます。