2019年(平成31年度)京都府公立高校入試【中期】試験数学問題の解説

2019年(平成31年度)京都府で行われた公立高校入試中期試験の数学問題の解説です。
問題は第1問から第6問まで全部で20問です。
問題はシンプルですが答えがすぐ出るのではなく、よく考えないと答えにたどり着かない問題もありますので問題の構成を見ながら要領よく処理しないと満点は厳しくなります。

問題は京都府で公開してくれています。

⇒　2019京都府中期数学問題

\(\,\large{1}\,\)は正の数負の数、無理数の計算、因数分解、方程式、円周角、確率の小問集合です。

後半に考えさせられる問題が控えていますのでちゃちゃっと済ませましょう。

『覚え太郎』会員向けに書いていますのでちょっと説明が不足するかもしれませんが、不明な点は学校の先生にでも聞いて下さい。
会員は直接質問して下さい。

1.小問集合（式の計算,方程式,円周角,確率）

(1)
かけ算、割り算は足し算引き算より先です。

途中の「－」は符号の「マイナス」ではなく演算を表す「引く」です。

　\(\hspace{10pt}(-6)^2\color{red}{-}4^2\div 2\\
=36\color{red}{-}(16\div 2)\\
=36\color{red}{-}8\\
=\underline{　28　}\)

(2)
通分して分母を1つにしますが分子には（かっこ）がついていることを忘れずにいてください。

　\(\hspace{10pt}\displaystyle \frac{3a+1}{4}-\frac{4a-7}{6}\\
\displaystyle =\frac{3(3a+1)-2(4a-7)}{12}\\
\displaystyle =\frac{9a+3-8a+14}{12}\\
\displaystyle =\underline{　\frac{a+17}{12}　}\)

(3)
無理数の計算です。

割り算が混じっていないので余計なことは考えず、ルートの中身を簡単にしてストレートに計算した方がはやいでしょう。

　\(\hspace{10pt}\color{red}{\sqrt{27}}+\color{blue}{\sqrt{24}}\times \color{magenta}{\sqrt{8}}\\
=\color{red}{3\sqrt{3}}+\color{blue}{2\sqrt{6}}\times \color{magenta}{2\sqrt{2}}\\
=3\sqrt{3}+4\color{red}{\sqrt{12}}\\
=3\sqrt{3}+4\times \color{red}{2\sqrt{3}}\\
=3\sqrt{3}+8\sqrt{3}\\
=\underline{　11\sqrt{3}　}\)

暗算するより素因数分解をしっかりやって、計算を進めた方が確実ではやいですよ。

(4)
移項して加減法でも良いですが、代入法の方がはやい形をしています。

　\( \begin{cases}
\hspace{7pt} \color{red}{x}=\color{blue}{2+y}　･･･①\\ \\
\hspace{7pt} 9\color{red}{x}-5y=2　･･･②
\end{cases}\)

①の\(\,x\,\)を②の\(\,x\,\)に代入しましょう。

　\(\begin{eqnarray}
9(\color{blue}{2+y})-5y&=&2\\
18+9y-5y&=&2\\
4y&=&2-18\\
&=&-16\\
y&=&\underline{　-4　}
\end{eqnarray}\)

\(\,x\,\)はこの\(\,y\,\)を①にもどした方がはやいですね。

　\(\begin{eqnarray}
x&=&2+(-4)\\
&=&2-4\\
&=&\underline{　-2　}
\end{eqnarray}\)

(5)
単なる因数分解です。
手順通り共通因数から抜き出します。

　\(\hspace{10pt}3a^2-24a+48\\
=3(a^2-8a+16)\\
=\underline{　3(a-4)^2　}\)

共通因数をむき出した後の（かっこ）の中の確認を忘れないようにしましょう。

(6)
直線の式を求めますが、「平行」なので傾きが同じです。
切片が分かっていないので切片を\(\,b\,\)とでもおきましょう。

　\(\displaystyle y=-\frac{2}{3}x+b\)

これが点\(\,(\,\color{red}{-6}\,,\,\color{blue}{2}\,)\,\)を通るので代入して

　\(\begin{eqnarray}\displaystyle
\color{blue}{2}&=&-\frac{2}{3}\times (\color{red}{-6})+b\\
2&=&4+b\\
-2&=&b
\end{eqnarray}\)

よって求める直線の式は

　\(\displaystyle \underline{　y=-\frac{2}{3}x-2　}\)

(7)
円周角と弧の関係です。

円の中心角は\(\,360°\,\)なので、円周の円周角は\(\,180°\,\)です。
（『覚え太郎』で確認して下さい。）

それさえ分ければ比例式を立てて解くだけです。

　\(\begin{eqnarray}\displaystyle
75:4\pi&=&180:x\\
75x&=&4\pi \times 180\\
x&=&\frac{4\pi \times 180}{75}\\
&=&\frac{4\pi 12}{5}\\
&=&\underline{　\frac{48\pi}{5}　}
\end{eqnarray}\)

円周角を見れば中心角に注目するのが普通なので、
円周角\(\,75°\,\)に対する中心角は\(\,150°\,\)で
中心角\(\,150°\,\)の弧が\(\,\color{red}{4\,\pi}\,\)なので
円の周の長さは

　\(\hspace{10pt}\displaystyle 4\pi\times \frac{360}{150}\\
\displaystyle =4\pi \times \frac{12}{5}\\
\displaystyle =\underline{　\frac{48\pi}{5}　}\)

と求めるのが普通でしょう。

どっちでも良いですよ。大して変わりません。

(3)
「少なくとも」という言葉を見れば高校生は余事象を考えるでしょうけど、
2019年に高校入試を受けている中学生にはまだなじみのない言葉です。

　「少なくとも\(\,1\,\)枚は表が出る」
ということは\(\,1\,\)枚でも表が出れば良いということで
　「表が\(\,1\,\)枚か\(\,2\,\)枚か\(\,3\,\)枚」
出ればいいので\(\,3\,\)通りが考えられます。

樹形図を書いてもたかが\(\,8\,\)通りなので樹形図を書くと良いです。

ここでは樹形図の代わりに表にします。
表を○、裏を×と表しておきます。

　\(\begin{array}{|c|c|c|c|} \hline
　1枚目　&　2枚目　&　3枚目　&　適･不適　\\ \hline
　○　&　○　&　○　&　\color{red}{適}　\\ \hline
　○　&　○　&　×　&　\color{red}{適}　\\ \hline
　○　&　×　&　○　&　\color{red}{適}　\\ \hline
　○　&　×　&　×　&　\color{red}{適}　\\ \hline
　×　&　○　&　○　&　\color{red}{適}　\\ \hline
　×　&　○　&　×　&　\color{red}{適}　\\ \hline
　×　&　×　&　○　&　\color{red}{適}　\\ \hline
　×　&　×　&　×　&　不適　\\ \hline
\end{array}\)

樹形図の方がはやいですね。
1つでも○があれば良いので

　\(\displaystyle \underline{　\frac{7}{8}　}\)

\(\,1\,\)枚も表が出ないのは\(\,3\,\)枚とも裏の場合で、
その確率は
　\(\displaystyle \frac{1}{8}\)

表が出るか裏が出るかはどちらかは必ず起こるので確率は全体では\(\,1\,\)です。

だから「表が\(\,1\,\)枚も出ない」というのが余事象といわれるもので

　\(\displaystyle 1-\frac{1}{8}=\underline{　\frac{7}{8}　}\)

と求めることが普通になってきますが、まだ良いです。

\(\,\large{1}\,\)は以上です。
　

2.資料（データ）の活用（代表値,階級値,ヒストグラム,読み取り）

\(\,\large{2}\,\)はデータの活用の基本問題です。

(1)
中央値を含む階級値を求めます。

中央値とはデータの値の小さい順に並べたときの、
値の小さい方、大きい方どちらから見ても真ん中にある値のことです。

ただ、度数分布表とデータそのものでは中央値の求め方は違いますので注意しましょう。

表は度数分布表です。

全体の度数（度数計）が\(\,29\,\)なので左右に分けると

　\(\,14\,\)人　｜　真ん中の人　｜　\(\,14\,\)人

と分けることができるので、小さい方からも大きい方からも\(\,15\,\)人目の値が中央値になります。

どちらから見ても同じですが、小さい方から\(\,15\,\)人目の人は、

　「\(\,6\,\)分以上\(\,12\,\)分未満の階級」

にいますので、中央値はその階級の階級値となります。

階級値は階級の真ん中の値なので

　\(\displaystyle \frac{6+12}{2}=\underline{　9　}　(分)\)
(2)
ヒストグラムを完成させる問題です。
ヒストグラムは階級の幅を横、度数を縦とした長方形を並べたものです。

\(\,2\,\)組の資料は\(\,30\,\)人分のデータが小さい順に与えられています。
これを階級ごとに度数を分けると、
（階級の以上、未満に注意して）
　\(\,3,4,5\,\)
　\(\,6,7,8,9,9,10,10,11\,\)
　\(\,12,12,13,13,13,14,15,15,16,16\,\)
　\(\,18,19,20,20,21,22,22\,\)
　\(\,25,27\,\)
と区切れるので

　\(\,0\,\)分以上\(\,6\,\)分未満　\(\,3\,\)人
　\(\,6\,\)分以上\(\,12\,\)分未満　\(\,8\,\)人　
　\(\,12\,\)分以上\(\,18\,\)分未満　\(\,10\,\)人　
　\(\,18\,\)分以上\(\,24\,\)分未満　\(\,7\,\)人　
　\(\,24\,\)分以上\(\,30\,\)分未満　\(\,2\,\)人

ヒストグラムは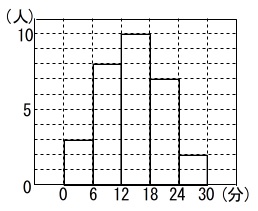（答え）

(3)
度数分布表と資料から必ず言えることをすべて答えます。

（ア）
通学時間が\(\,18\,\)分未満の人数は

\(\,1\,\)組
　\(\,5+11+6=22\,\)

\(\,2\,\)組
　\(\,3+8+10=21\,\)

\(\,2\,\)組の方が少ないので言えない。×

（イ）
通学時間が\(\,24\,\)分以上の生徒の割合は

\(\,1\,\)組
　\(\displaystyle \frac{2}{29}\)

\(\,2\,\)組
　\(\displaystyle \frac{2}{30}\)

度数（分子）は同じですが、
度数合計（分母）は\(\,1\,\)組の方が少ないので、
割合は\(\,1\,\)組の方が大きい。○

（ウ）
\(\,1\,\)組の\(\,6\,\)分以上\(\,18\,\)分未満の人数は
　\(\,11+6=17\,\)

\(\,2\,\)組の\(\,12\,\)分以上\(\,24\,\)分未満の人数は
　\(\,10+7=17\,\)

同じ人数です。○

（エ）
通学時間が最も短い生徒は、\(\,2\,\)組は\(\,3\,\)分と分かります。

しかし、\(\,1\,\)組の最も短い人は\(\,0\,\)分以上\(\,6\,\)分未満としか分かっていないので\(\,1\,\)分か\(\,2\,\)分かもしれない。

度数分布表では階級値と見なして資料集計しますが、個別データが分かるわけではないので階級値だと言い切ることはできません。

よって、最も短い人は\(\,3\,\)分とは言えない。×

（オ）
\(\,1\,\)組\(\,2\,\)組全員の中で大きい方から\(\,16\,\)番目の人は、

\(\,1\,\)組が\(\,18\,\)分以上\(\,30\,\)分未満に\(\,7\,\)人
\(\,2\,\)組が\(\,18\,\)分以上\(\,30\,\)分未満に\(\,9\,\)人

いるので\(\,2\,\)組の\(\,18\,\)分という人はこの階級の一番小さい値なので\(\,16\,\)番目の可能性があります。

階級には幅があるので断言はできませんが、
もし、\(\,1\,\)組に\(\,18\,\)分という人がいたとしても、
大きい方から\(\,16\,\)番目が\(\,18\,\)分というのは変わりません。○

答え　\(\,\underline{　（イ）（ウ）（オ）　}\,\)

\(\,\large{2}\,\)のデータの活用は以上です。

次は回転体の表面積と体積比です。

3.回転体の表面積と体積比

(1)(2)ともに回転体なので見取り図を簡単にでも書いておくと分かり易いです。

与えられた長さと、条件から分かる長さを出しておきましょう。

\(\,Ⅰ図\,\)の回転体は半径\(\,\displaystyle \color{red}{\frac{3}{2}}\,\)の球です。

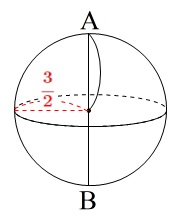
\(\,Ⅱ図\,\)の回転体は、円柱と円錐の合わさった立体になります。
どちらも底面の半径は\(\,2\,\)です。
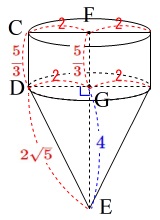このとき、三平方の定理から

　\(\begin{eqnarray}
\mathrm{DG^2+\color{blue}{GE}^2}&=&\mathrm{DE^2}\\
2^2+\mathrm{\color{blue}{GE}^2}&=&(2\sqrt{5})^2\\
4+\mathrm{\color{blue}{GE}^2}&=&20\\
\mathrm{\color{blue}{GE}^2}&=&20-4\\
&=&16\\
\mathrm{\color{blue}{GE}}&=&\color{blue}{4}　(\mathrm{GE}＞0)
\end{eqnarray}\)

ここまで出しておけば、すべての表面積と体積は出ます。

(1)
立体\(\,\mathrm{X}\,\)の表面積を求めます。

半径\(\,\displaystyle \frac{3}{2}\,\)の球の表面積を求めよ、ということです。

球の表面積と体積は公式を使わないと中学生は求めることはできません。

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

半径\(\,r\,\)の球の表面積\(\,S\,\)は、

　\(\displaystyle \color{red}{S=4\,\pi\,r^2}\)

なので求める表面積は

　\(\hspace{10pt}\displaystyle 4\,\pi\,\times \left(\frac{3}{2}\right)^2\\
\displaystyle =\underline{　9\,\pi　}　(\mathrm{cm^2})\)

(2)
球\(\,\mathrm{X}\,\)と\(\,Ⅱ図\,\)の回転体\(\,\mathrm{Y}\,\)の体積比を求めます。

\(\,\mathrm{X}\,\)の体積は半径\(\,\frac{3}{2}\,\)の球の体積なので

　\(\hspace{10pt}\displaystyle \frac{4}{3}\,\pi\,\left(\frac{3}{2}\right)^3\\
\displaystyle =\frac{4}{3}\,\pi\,\frac{27}{8}\\
\displaystyle =\color{magenta}{\frac{9}{2}\,\pi}\)

立体\(\,\mathrm{Y}\,\)は円柱と円錐の合体した立体です。

立体\(\,\mathrm{Y}\,\)の体積は

　\(\hspace{10pt}\displaystyle \pi\,(\color{red}{2})^2\times \color{red}{\frac{5}{3}}+\frac{1}{3}\times \pi\,(\color{red}{2})^2\times \color{blue}{4}\\
\displaystyle =\frac{20}{3}\,\pi+\frac{16}{3}\,\pi\\
\displaystyle =\frac{20+16}{3}\,\pi\\
=\color{magenta}{12\,\pi}\)

よって立体\(\,\mathrm{X}\,\)と立体\(\,\mathrm{Y}\,\)の体積比は

　\(\begin{eqnarray}\displaystyle
\mathrm{X:Y}&=&\color{magenta}{\frac{9}{2}\,\pi}:\color{magenta}{12\,\pi}\\
&=&9:24\\
&=&\underline{　3:8　}
\end{eqnarray}\)

\(\,\large{3}\,\)は以上です。

一気にやっておきたいですが、この後が長くなるので分けます。

⇒　2019年京都府公立高校入試【中期】試験数学問題の解説(後半)

\(\,\large{4}\,\)は制動距離の問題で教科書にもある\(\,y\,\)が\(\,x\,\)の2乗に比例する問題ですが、少しひねってあります。

\(\,\large{5}\,\)は折り返しを含む合同と相似の総合問題です。

\(\,6\,\)は格子点の問題ですが規則性をテーマとしているのでしょう。

ちょっと手を加えれば大したことはありません。

⇒　京都府公立高校入試数学の過去問と解答解説

\(\,2018\,\)年の京都府の前期と比べれば規則性としては非常に簡単です。笑