福岡県公立高校入試2019年(平成31年度)数学問題の解説【後半】

2019年(平成31年度)福岡県で行われた公立高校入試数学問題の後半の解説です。
第4問は1次関数、第5問は円に内接する三角形の合同と相似、第6問は回転体の体積と線分の長さ問題です。
多少手こずりそうな問題もありますが関数、平面図形、空間図形の基本的な取り組み方を身につけるには良い問題です。

問題は福岡県で公開してくれています。

⇒　2019福岡県数学問題

移動距離と1次関数の交点の求め方

\(\color{black}{\fbox{　4　}}\)　\(\,1\,\)次関数を利用して移動について考える問題です。

注意しておきたいのは関数ではいつも同じですが、
\(\,x\,\)が何を表し、\(\,y\,\)が何を表しているかをしっかり見ておくことです。

\(\,\mathrm{A}\,\)さんが家から学校まで移動するときの状態が書いてあるのでまとめてみましょう。
（長さの単位は「\(\,m\,\)」ですが省略します。）

\(\,\mathrm{A}\,\)さんの移動状態

　\(\,\mathrm{A}\,\)さんの家から学校まで距離は\(\,2100\,\)
　家を出発し\(\,9\,\)分間歩き、
　続いて分速\(\,60\,\)で\(\,14\,\)分間歩き、
　残りの\(\,540\,\)を分速\(\,90\,\)で歩く。

家から学校まで\(\,29\,\)分かかったことは問題にも書いてあります。

\(\,\mathrm{A}\,\)さんは\(\,7\,\)時\(\,30\,\)分に出発していますが、かかった時間で考えていることに注意して下さい。
関数にしたときは\(\,\mathrm{A}\,\)さんの出発時刻が\(\,x=0\,\)となります。

(1)
表がなくても線分図を書いて\(\,9\,\)分後の\(\,\mathrm{A}\,\)さんの位置は求まりますが、

せっかく表を与えてくれているので利用しましょう。

　\(\begin{array}{|c|c|c|c|} \hline
　時間　&　0　&　1　&　2　\\ \hline
　距離　&　2100　&　2020　&　1940　\\ \hline
\end{array}\)

\(\,1\,\)分間で（\(\,9\,\)分まで\(\,1\,\)分間の移動距離は一定です。）
　\(\hspace{10pt}2100-2020\\
=2020-1940\\
=80\)

なので\(\,9\,\)分間では

　\(\hspace{10pt}80\times 9\\
=720\)

よって学校までの残りの距離は

　\(\hspace{10pt}2100-720\\
=\underline{　1380　}　(m)\)

(2)
\(\,\mathrm{B}\,\)さんの移動です。

　\(\,\mathrm{B}\,\)さんの家から学校まで\(\,1700\,\)。
　\(\,7\,\)時\(\,39\,\)分に家を出発し分速\(\,75\,\)で歩いた。

\(\,7\,\)時\(\,39\,\)分は関数の\(\,x=9\,\)のときです。

\(\,\mathrm{B}\,\)さんの出発したときの座標は

　\((\,9\,,\,1700\,)\)

\(\,\mathrm{B}\,\)さんが出発してから\(\,7\,\)時\(\,53\,\)分までは\(\,14\,\)分間あるので、
移動した距離は

　\(\hspace{10pt}75\times 14\\
=1050\)

学校までの残りの距離は

　\(\hspace{10pt}1700-1050\\
=650\)

\(\,7\,\)時\(\,53\,\)分は座標上では\(\,x=23\,\)になるので、
\(\,\mathrm{B}\,\)さんの\(\,7\,\)時\(\,53\,\)分の座標は

　\((\,23\,,\,650\,)\)

\(\,\mathrm{B}\,\)さんの学校までの距離を関数にしたものは明らかですね。
\(\,\mathrm{B}\,\)さんのこの\(\,9\,\)分間の速さは\(\,\mathrm{A}\,\)さんよりはやいので傾きで決定的になります。

　\(\,\underline{　イ　}\,\)

(3)
\(\,\mathrm{C}\,\)さんの移動の状態が書かれています。

速さは書いてはありませんが距離と時間があるので求めることができます。

\(\,\mathrm{C}\,\)さんの状態

　\(\,\mathrm{C}\,\)さんの家から学校までの距離は\(\,630\,\)
　\(\,7\,\)時\(\,50\,\)分に家を出発し\(\,8\,\)時に学校に着いた。

「\(\,7\,\)時\(\,53\,\)分から\(\,7\,\)時\(\,59\,\)分までに\(\,\mathrm{A}\,\)さんに追いつかれ」、
とありますがこの間に\(\,\mathrm{A}\,\)さんの直線と\(\,\mathrm{C}\,\)さんの関数を表す直線が交点を持つという意味です。

これは後で考えましょう。

\(\,\mathrm{C}\,\)さんの移動を表す直線を求めましょう。

\(\,7\,\)時\(\,50\,\)分は\(\,x=20\,\)を意味します。
このとき学校までの距離は\(\,630\,\)なので

　\((\,20\,,\,630\,)\)

学校に着いたのは\(\,8\,\)時\(\,0\,\)分(\(\,7\,\)時\(\,60\,\)分)なので、
そのときの座標は

　\((\,30\,,\,0\,)\)

よって\(\,\mathrm{C}\,\)さんの移動を表す関数はこの\(\,2\,\)点を通るので

　\(\begin{eqnarray}
y-630&=&\frac{\,0-630\,}{\,30-20\,}(x-20)\\
y&=&-63x+1260+630\\
&=&-63x+1890
\end{eqnarray}\)

この直線の求め方はいつも通り、傾きを出して、切片を出す順序で求めて良いです。

\(\,2\,\)点
　\((\,20\,,\,630\,)\)
　\((\,30\,,\hspace{6pt}0\hspace{6pt})\)
を通る直線です。

傾きは変化の割合と同じなので

　\(\,x\,の増加量=30-20=\color{red}{10}\,\)
　\(\,y\,の増加量=0-630=\color{blue}{-630}\,\)

（増加量は同じ方向に効かないと傾きは符号が逆になりますよ。）

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

　\(\begin{eqnarray}\displaystyle
(傾き)=\frac{\color{blue}{-630}}{\color{red}{10}}\\
=-63
\end{eqnarray}\)

切片を\(\,\color{magenta}{b}\,\)とすると

　\(y=-63x+\color{magenta}{b}\)

これが\(\,2\,\)点を通るのでどちらかを代入します。

　\((\,30\,,0\,)\)

を代入しましょう。

　\(\begin{eqnarray}
0&=&-63\times (30)+\color{magenta}{b}\\
&=&-1890+\color{magenta}{b}\\
\color{magenta}{b}&=&1890
\end{eqnarray}\)

という方法で直線は求められる、として省略しました。笑

条件通りに解答をまとめておきます。
（条件\(\,Ⅰ\,\),\(\,Ⅱ\,\),\(\,Ⅲ\,\)を満たしていれば良いので書き方はいろいろあって良いですよ。）

解答例

　\(\,\mathrm{A}\,\)さんが家を出発してからの時間を\(\,x\,\)、学校までの残りの距離を\(\,y\,\)とする。

\(\,23≦x≦29\,\)における\(\,\mathrm{A}\,\)さんの移動を表す関数は、
\(\,2\,\)点
　　\((\,23\,,\,540\,)\)　\((\,29\,,\,0\,)\)
を通るので
　\(y=-90x+2610　･･･①\)

\(\,\mathrm{C}\,\)さんの移動を表す関数は、
\(\,2\,\)点
　　\((\,20\,,\,630\,)\)　\((\,30\,,\,0\,)\)
を通るので
　\(y=-63x+1890　･･･②\)

①②の交点は、連立すると
　\(\displaystyle (\,x\,,\,y)=\left(\frac{80}{3}\,,\,210\,\right)\)

この\(\displaystyle \,x=\frac{80}{3}\)は\(\,7\,\)時\(\,56\,\)分\(\,40\,\)秒を意味し、
「\(\,7\,\)時\(\,53\,\)分から\(\,7\,\)時\(\,59\,\)分までの間に」\(\,\mathrm{C}\,\)さんが\(\,\mathrm{A}\,\)さんに追いつかれた条件に適している。

答え　\(\underline{　\,7\,時\,56\,分\,40\,秒　}\,\)

関数問題はすべての関数と、交点をすべて求める方向で考えれば方針は立ちます。
この問題では\(\,\mathrm{A}\,\)さんの場合、3つの関数があることは気をつけておきましょう。

合同の発見と相似の利用方法

\(\color{black}{\fbox{\(　5　\)}}\)　は合同と相似と円周角の定理のちょっとした応用です。

(1)に入る前の条件は問題すべてに通じる条件です。

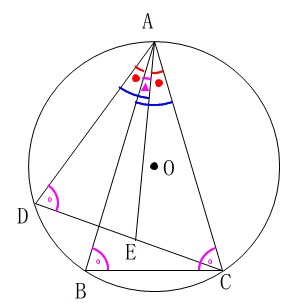
図\(\,1\,\)にある条件を図示しておきましょう。

合同や相似の証明は図の中で完成させるというのが基本です。
図の中で示せないものは日本文でも示せません。

条件は

　\(\,4\,\)点\(\,\mathrm{A,B,C,D}\,\)は円周上の点　
　\(\,\mathrm{AB=AC}\,\)
　\(\,\mathrm{∠EAC=∠DAB}\,\)
頂点\(\,\mathrm{D}\,\)も円周上の点であることから円周角の等しいところがいろいろと出てきます。
全部を書き込むと見にくくなるので、\(\,\mathrm{△ABC}\,\)が二等辺三角形なので底角が等しいことも加えて書き込みます。

すでに合同な三角形や相似な三角形は見えていますね。

(1)
　\(\,\mathrm{AB=AC}\,\)
　\(\,\mathrm{∠DAB=∠EAC}\,\)
　\(\,\mathrm{∠ABD=∠ACE}\,\)
\(\,1\,\)辺とその両端の角がそれぞれ等しいので
　\(\,\underline{　\mathrm{△ABD}　}　\equiv　\underline{　\mathrm{△ACE}　}\,\)

合同な図形の対応する辺は等しいので、
　\(\,\mathrm{AD=AE}\,\)

(2)
「下線部②であることを証明せよ。」
とは、
　\(\,\mathrm{△ADE}\,\)　∽　\(\,\mathrm{△ABC}\,\)
の証明です。

証明は後でしますが、何故相似を証明することで\(\,\mathrm{AD=AE}\,\)が言えるか？

　\(\,\mathrm{△ABC}\,\)が\(\,\mathrm{AB=AC}\,\)の二等辺三角形だから
　\(\,\mathrm{△ADE}\,\)も\(\,\mathrm{AD=AE}\,\)の二等辺三角形だということが言える。

ということです。

証明しておきます。

　\(\,\mathrm{△ADE}\,\)　と　\(\,\mathrm{△ABC}\,\)　において

円周角の定理により\(\,\stackrel{\frown}{\mbox{AC}}\,\)の円周角は等しいので
　\(\mathrm{∠ADE=∠ABC}　･･･①\)

また、\(\,\mathrm{∠DAE}\,\)　と　\(\,\mathrm{∠BAC}\,\)　において
　\(\,\mathrm{∠DAE=∠DAB+\color{red}{∠BAE}}\,\)
　\(\,\mathrm{∠BAC=∠EAC+\color{red}{∠BAE}}\,\)
仮定から
　\(\,\mathrm{∠DAB=∠EAC}\,\)
なので
　\(\,\mathrm{∠DAE=∠BAC}　･･･②\,\)

①②により
　\(\,2\,\)組の角がそれぞれ等しい
ので
　\(\,\mathrm{△ADE}\,\)　∽　\(\,\mathrm{△ABC}\,\)

どちらも二等辺三角形だということが示せたので、
　\(\mathrm{AD=AE}\)

(3)
図\(\,1\,\)に条件が加わります。

　\(\,\mathrm{∠BAC=60^{\circ}}\,\)
　\(\,\mathrm{\stackrel{\frown}{\mbox{AD}}\,:\,\stackrel{\frown}{\mbox{DB}}=3:1}\,\)
　円\(\,\mathrm{O}\,\)の半径は\(\,4\,\)

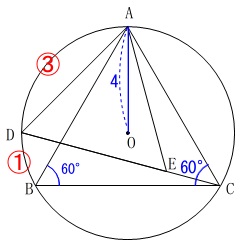
　\(\,\mathrm{\stackrel{\frown}{\mbox{AD}}\,:\,\stackrel{\frown}{\mbox{DB}}=3:1}\,\)
であることから
　\(\,\mathrm{∠ACD\,:\,∠BCD=3:1}\,\)

また\(\,\mathrm{△ABC}\,\)は正三角形なので
　\(\,\mathrm{∠ACB=60^{\circ}}\,\)
だから
　\(\,\mathrm{∠ACD=45^{\circ}}\,\)
　\(\,\mathrm{∠BCD=15^{\circ}}\,\)

このとき中心角は円周角の\(\,2\,\)倍なので、

　\(\,\mathrm{∠AOD=90^{\circ}}\,\)
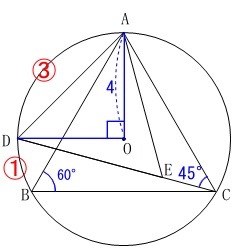ここまでくればいろいろと長さは求まりますが、
求めるのは\(\,\mathrm{△ADC}\,\)の面積だけなので、正三角形と三角定規だけで良いでしょう。

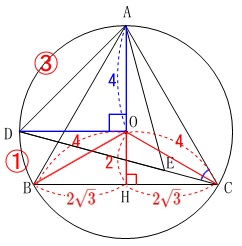\(\,\mathrm{△OCH}\,\)は三角定規なので
　\(\,\mathrm{OA=OB=OC=4}\,\)
から
　\(\,\mathrm{OH=2}\,\)
　\(\,\mathrm{CH=2\sqrt{3}}\,\)

ここで\(\,\mathrm{△ADC}\,\)を3つに分けます。

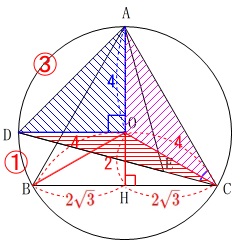
　\(\mathrm{△ADC=△AOD+△AOC+△DOC}\)

と分けてみると
　
\(\,\mathrm{△AOD}\,\)は\(\,\mathrm{DO}\,\)を底辺とし、\(\,\mathrm{AO}\,\)を高さとする三角形

　\(\begin{eqnarray}\displaystyle
\mathrm{△AOD}&=&\frac{1}{2}\times \mathrm{DO}\times \mathrm{AO}\\
&=&\frac{1}{2}\times 4\times 4\\
&=&\color{red}{8}　
\end{eqnarray}\)

\(\,\mathrm{△AOC}\,\)は\(\,\mathrm{AO}\,\)を底辺とし、\(\,\mathrm{CH}\,\)を高さとする三角形

　\(\begin{eqnarray}\displaystyle
\mathrm{△AOC}&=&\frac{1}{2}\times \mathrm{AO}\times \mathrm{CH}\\
&=&\frac{1}{2}\times 4\times 2\sqrt{3}\\
&=&\color{red}{4\sqrt{3}}　
\end{eqnarray}\)

\(\,\mathrm{△DOC}\,\)は\(\,\mathrm{DO}\,\)を底辺とし、\(\,\mathrm{OH}\,\)を高さとする三角形

　\(\begin{eqnarray}\displaystyle
\mathrm{△DOC}&=&\frac{1}{2}\times \mathrm{DO}\times \mathrm{OH}\\
&=&\frac{1}{2}\times 4\times 2\\
&=&\color{red}{4}　
\end{eqnarray}\)

なので

　\(\begin{eqnarray}
\mathrm{△ADC}&=&\mathrm{△AOD+△AOC+△DOC}\\
&=&\color{red}{8}+\color{red}{4\sqrt{3}}+\color{red}{4}\\
&=&\underline{　12+4\sqrt{3}　}　(\mathrm{cm^2})
\end{eqnarray}\)

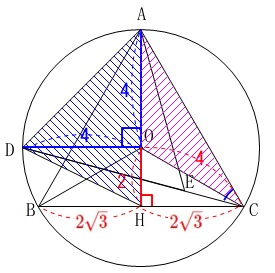\(\,\mathrm{△DOC=△DOH}\,\)なので

　\(\begin{eqnarray}
\mathrm{△ADC}&=&\mathrm{△ADH+△AOC}\\
&=&\frac{1}{2}\times 6\times 4+\frac{1}{2}\times 4\times 2\sqrt{3}\\
&=&\underline{　12+4\sqrt{3}　}　(\mathrm{cm^2})
\end{eqnarray}\)

でも良いですし、他にもありますが、
数値もそれほど大きいものではありませんので、思い立った方法で突っ走った方が試験会場でははやいでしょう。

回転体の体積と空間図形の線分の長さ

\(\color{black}{\fbox{\(\,　\large{6}　\,\)}}\)　は回転体の体積と線分ですが「立体」の考え方といって良いでしょう。

図\(\,1\,\)から見ていきます。

　底面の半径\(\,6\,\)、高さ\(\,4\,\)の円錐
と
　底面の半径\(\,6\,\)、高さ\(\,5\,\)の円柱
を合わせた立体です。

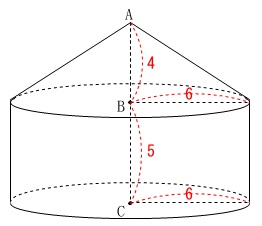
(1)立体の体積を求めます。

円錐と円柱の体積を合わせれば良いだけです。

底面積はどちらも
　\(\pi\, (6)^2=36\,\pi\)
なので

　\(\hspace{10pt}\displaystyle \frac{1}{3}\times 36\,\pi \times 4+36\,\pi\times 5\\
=48\,\pi+180\,\pi\\
=\underline{　228\,\pi　}　(\mathrm{cm^2})\)

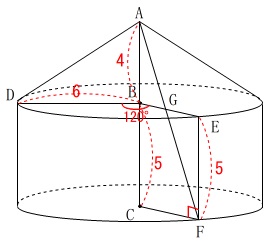
図\(\,2\,\)は、

　円\(\,\mathrm{B}\,\)の周上に\(\,\mathrm{D,E}\,\)を
　　\(\,\mathrm{∠DBE=120^{\circ}}\,\)
　円\(\,\mathrm{C}\,\)の周上に点\(\,\mathrm{F}\,\)を
　　\(\,\mathrm{∠BEF=90^{\circ}}\,\)
　線分\(\,\mathrm{AF}\,\)と\(\,\mathrm{BE}\,\)の交点を\(\,\mathrm{G}\,\)

となるように取ります。
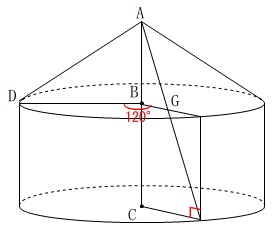これに長さを書き込んでおきます。

(2)
\(\,\mathrm{△ABG}\,\)の面積は\(\,\mathrm{△ACF}\,\)の面積の何倍か？

面積を求める必要はありません。
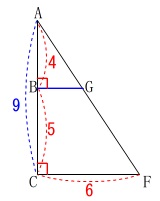
\(\,\mathrm{△ACF}\,\)を抜き出して見てみると

　\(\,\mathrm{△ABG}\,\)　∽　\(\,\mathrm{△ACF}\,\)

で相似比は

　\(\mathrm{AB:AC=\color{red}{4}:\color{blue}{9}}\)
なので面積比は

　\(\begin{eqnarray}
\mathrm{△ABG:△ACF}&=&\color{red}{4}^2:\color{blue}{9}^2\\
&=&16:81
\end{eqnarray}\)

よって\(\,\mathrm{△ABG}\,\)の面積は\(\,\mathrm{△ACF}\,\)の

　\(\displaystyle \underline{　\frac{16}{81}　倍　}\)

(3)
さらに条件が加わります。

　\(\,\mathrm{AD}\,\)の中点を\(\,\mathrm{M}\,\)とする。
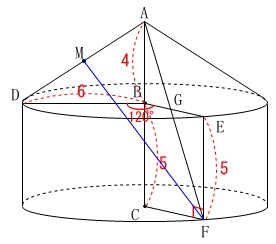このときの線分\(\,\mathrm{MF}\,\)を求めます。

線分\(\,\mathrm{AF}\,\)と線分\(\,\mathrm{MF}\,\)を実線で書いていますが、立体の中を通っているので注意して下さい。
\(\,\mathrm{△ADF}\,\)を抜き出してパップスでも簡単に出せますが、\(\,\mathrm{DF}\,\)の長さはまだ出ていません。

\(\,\mathrm{DF}\,\)の長さは\(\,\mathrm{△DBE}\,\)を抜き出して\(\,\mathrm{DE}\,\)を求め、
直角三角形\(\,\mathrm{△DEF}\,\)から\(\,\mathrm{DF}\,\)を三平方の定理を利用すれば出てきます。

ここでは少し見方を変えておきます。

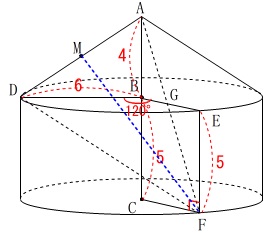
\(\,\mathrm{M}\,\)から補助線として垂線を引きましょう。

\(\,\mathrm{M}\,\)から底面の円\(\,\mathrm{C}\,\)に垂線を引いて交点を\(\,\mathrm{H}\,\)とします。
\(\,\mathrm{△MHF}\,\)に三平方の定理を利用する方向で考えましょう。

線分\(\,\mathrm{MH}\,\)は\(\,\mathrm{AB=4}\,\)から\(\,\mathrm{MI=2}\,\)とわかるので

　\(\mathrm{MH}=2+5=7\)

あとは\(\,\mathrm{HF}\,\)が分かれば三平方の定理が使えます。

底面の\(\,\mathrm{△CHF}\,\)を抜き出します。
このとき\(\,\mathrm{CH}\,\)の延長と\(\,\mathrm{F}\,\)から直線\(\,\mathrm{CH}\,\)に下ろした垂線の交点を\(\,\mathrm{K}\,\)とすると、
\(\,\mathrm{△CFK}\,\)は三角定規になります。
半径の\(\,\mathrm{CF=6}\,\)から

　\(\,\mathrm{CK=3}\,\)
　\(\,\mathrm{FK=3\sqrt{3}}\,\)

となるので三平方の定理から

　\(\begin{eqnarray}
\mathrm{\color{red}{HF^2}}&=&\mathrm{HK^2+FK^2}\\
&=&6^2+(3\sqrt{3})^2\\
&=&36+27\\
&=&\color{red}{63}\\
\end{eqnarray}\)

\(\,\mathrm{HF\,＞\,0}\,\)より

　\(\mathrm{HF}=\color{blue}{3\sqrt{7}}\)

\(\,\mathrm{HF}\,\)は求めても良いですが再度三平方の定理を使うので平方のままでも良いですよ。

\(\,\mathrm{△HMF}\,\)に三平方の定理を使って\(\,\mathrm{MF}\,\)を求めます。

　\(\begin{eqnarray}
\mathrm{MF^2}&=&\mathrm{MH^2+\color{red}{HF^2}}\\
&=&7^2+(3\sqrt{7})^2\\
&=&49+\color{red}{63}\\
&=&112
\end{eqnarray}\)

\(\,\mathrm{MF\,＞\,0}\,\)より

　\(\,\mathrm{MF}=\underline{　4\sqrt{7}　(\mathrm{cm})　}\,\)

素因数分解はていねいに、確実にやった方が良いですよ。

『覚え太郎』会員は\(\,\mathrm{△ADF}\,\)にパップスを利用する方法も試してみて下さい。

\(\,\mathrm{△BDE}\,\)は三角定規2つ分であることと、
\(\,\mathrm{△DEF}\,\)に三平方の定理を使うと\(\,\mathrm{DF}\,\)が出ます。

いずれにしても立体では平面を抜き出して考えることがポイントですよ。

長くなりましたが、\(\,2019\,\)年福岡県の公立入試数学は以上です。

⇒　福岡県公立高校入試2019年(平成31年度)数学問題の解説

前半からの時間配分を考えて、しっかり作業すれば方針は立てやすいです。

⇒　福岡県公立高校入試数学過去問の解答解説

\(\,2018\,\)年もバランス良く出題されていました。

変な難問ではなく、基本の確認と手を動かすことが大切だと知るには良い応用問題の組み合わせとなっていますね。