2019年京都府公立高校(前期)入試の数学問題の解説

2019年(平成31年度)に京都府で行われた公立高校入試の前期数学問題の解説です。
第1問から第6問まであり問題数、計算ともに力のいる問題がそろっています。
さらに、方針によっては時間を要する問題もありますので相当な練習問題と対策が必要です。
だからといって、めったやたらに問題数を増やせば良いというわけではありませんよ。

問題は京都府も公開してくれています。

⇒　2019京都府【前期】問題

問題のレベルから受験する中学生の力はある程度あるものとして、
解説を少し省略させて頂きます。笑

1.小問集合

\(\,\large{1}\,\)は小問集合で(1)から(3)数と式の計算、(4)代入、(5)2次方程式、(6)球の表面積、(7)放物線の定義域、値域、(8)近似値、(9)平行線の角度、となっています。

難しくはありませんがミスをしそうな問題が並んでいますのでいい加減に計算しない方が良いですよ。

数と式の計算問題

(1)
\(\hspace{10pt}\displaystyle \{5-(-2^2)\}\div\left(\frac{3}{4}\right)^2\\
\displaystyle =\{5-(-4)\}\div\left(\frac{9}{16}\right)\\
\displaystyle =9\times \frac{16}{9}\\
=\underline{　16　}\)

（かっこ）の中が先で、割り算は逆数のかけ算、という基本通りの計算をしました。

(2)
　\(\hspace{10pt}\displaystyle \frac{7x-1}{5}-x+2\\
\displaystyle =\frac{(7x-1)+5(-x+2)}{5}\\
\displaystyle =\frac{7x-1-5x+10}{5}\\
\displaystyle =\underline{　\frac{2x+9}{5}　}\)

通分しただけです。
分母は1つにして、分子の計算に集中するのがはやいですよね。

(3)
　\(\hspace{10pt}\displaystyle (3-\sqrt{5})^2+\frac{10}{\sqrt{5}}\\
\displaystyle =(9-6\sqrt{5}+5)+\frac{10\sqrt{5}}{5}\\
\displaystyle =14-6\sqrt{5}+2\sqrt{5}\\
=\underline{　14-4\sqrt{5}　}\)

慣れていれば\(\,2\,\)行目は飛ばして良いですが、
ミスしないためにも\(\,2\,\)乗展開、有理化は確実にやった方が良いですよ。

代入計算問題と2次方程式の解

(4)
前期問題受験生で\(a=30\,,\,b=-23\,\)をそのまま代入するなんて算数するくらいならこの問題は捨てた方が良いです。
高校の数学で撃沈することは目に見えています。

落ち着いて、少しだけでも工夫しましょう。

因数分解してから代入してみましょう。

　\(\hspace{10pt}(\color{red}{a-2b})^2-2(\color{red}{a-2b})-24\\
=\{(\color{red}{a-2b})+4\}\{(\color{red}{a-2b})-6\}\\
=(a-2b+4)(a-2b-6)\\
=\{(30-2(-23)+4\}\{(30-2(-23)-6\}\\
=(30+46+4)(30+46-6)\\
=80\times 70\\
=\underline{　5600　}\)

直接代入してみると、

　\(\hspace{10pt}(a-2b)^2-2(a-2b)-24\\
=\{(30)-2(-23)\}^2-2\{(30-2(-23)\}-24\\
=(30+46)^2-2(30+46)-24\\
=76^2-2\times 76-24\\
=5776-152-24\\
=5776-176\\
=\underline{　5600　}\)

条件の数値が大きくなったときのことを考えて工夫する、それが数学です。

(5)
\(\,2\,\)次方程式の解を求めるときは因数分解を利用することを第\(\,1\,\)に考えて良いですが、
　\(3x^2-3x-2=0\)
共通因数もなく、因数分解できないので解の公式です。

⇒　２次方程式を解の公式で解く問題の見分け方と例題

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-3)\pm \sqrt{(-3)^2-4\cdot (3)\cdot (-2)}}{2\cdot 3}\\
&=&\frac{3\pm \sqrt{9+24}}{6}\\
&=&\underline{　\frac{3\pm \sqrt{33}}{6}　}
\end{eqnarray}\)

球の表面積と相似比

(6)
球はすべて相似です。

なので表面積も相似比の\(\,2\,\)乗に比例します。
球\(\,\mathrm{A}\,\)の表面積を\(\,\mathrm{S_A}\,\)などと表すことにします。

　\(\mathrm{S_A:S_B}=9:1\)

なので相似比は\(\,3:1\,\)です。

よって球\(\,\mathrm{A}\,\)の半径を\(\,r\,\)とすると球\(\,\mathrm{B}\,\)の半径が\(\,4\,\)だから

　\(\begin{eqnarray}
r:4&=&\color{red}{3:1}\\
r&=&\underline{　12　}　(\mathrm{cm})
\end{eqnarray}\)

関数の定義域と値域

(7)
関数は原点を頂点とする\(\,2\,\)次関数です。

値域（\(\,y\,\)の変域）が
　\(\displaystyle -8\,≦\,y≦\,-\frac{1}{18}\)
なので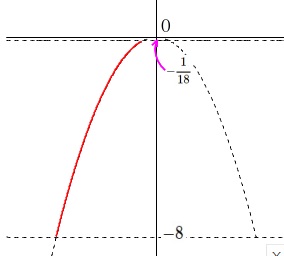
定義域（\(\,x\,\)の変域）の上限\(\,p\,\)は\(\,0\,\)より小さいはずです。

よって
　\(\,x=-2\,\)のとき最小値\(\,y=-8\,\)
　\(\,x=p\,\)のとき最大値\(\displaystyle \,-\frac{1}{18}\,\)

このことから
　\(\begin{eqnarray}\displaystyle -\frac{1}{18}&=&-2(p)^2\\
\frac{1}{36}&=&p^2\\
p&=&\underline{　-\frac{1}{6}　}
\end{eqnarray}\)

近似値と誤差

真の値\(\,a\,\)が存在する範囲を数直線で表せばすぐに終わります。

⇒　近似値とは？誤差の大きさと真の値の範囲の表し方(資料の活用)

小数第\(\,2\,\)位を四捨五入\(\,3.1\,\)になるので
上限の\(\,3.15\,\)を含まなければ良いので、

　\(3.05\,≦\,a\,\color{black}{\fbox{\(　＜　\)}}\,\color{black}{\fbox{\(　3.15　\)}}\)

答え　\(\,\underline{　\mathrm{A}\,（ア）＜　\mathrm{X}\,（ク）3.15　}\,\)

角の二等分線と平行線の角度

問題に必要無い条件はありません。

　\(\ell\,/\!/\,m\)
　\(\mathrm{AD}\)は\(\,\mathrm{∠BAC}\,\)の二等分線

平行線で角度、であれば錯角か同位角を使うでしょう。
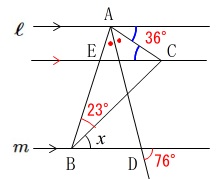同位角が等しいことから

　\(\begin{eqnarray}
\mathrm{∠DAC}+36^{\circ}&=&76^{\circ}\\
\mathrm{∠DAC}&=&76^{\circ}-36^{\circ}\\
&=&40^{\circ}
\end{eqnarray}\)

このとき
　
　\(\mathrm{∠BAC}=80^{\circ}\)

錯角が等しいことから

　\(\mathrm{∠ACE}=36^{\circ}\)

ここまで出せば三角形の内角の和でも、平行線の錯角でも何でも良いです。

錯角が等しいことから

　\(\begin{eqnarray}
x+23^{\circ}&=&180^{\circ}-(36^{\circ}+80^{\circ})\\
&=&180^{\circ}-116^{\circ}\\
&=&64^{\circ}\\
x&=&64^{\circ}-23^{\circ}\\
&=&\underline{　41^{\circ}　}
\end{eqnarray}\)

\(\,\large{1}\,\)の小問集合は以上です。

2.さいころ2つの確率

2つのさいころを投げる場合なのでルールを読み取れれば簡単です。

【ルール】

　同じ目が出たらその目と同じ番号の箱に玉を\(\,1\,\)個入れる。
　違う目が出たらその小さい方と大きい方の目の間にも玉を入れる。

それだけです。

樹形図で良いですがさいころ2つは表が便利ですね。

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
&\,1\,&\,2\,&\,3\,&\,4\,&\,5\,&\,6\,\\ \hline
\,1\,& &　& & & & \\ \hline
2& &　& & & & \\ \hline
3& &　& & & & \\ \hline
4& & & & & & \\ \hline
5& & & & & & \\ \hline
6& & & & & & \\ \hline
\end{array}\)

(1)
\(\,6\,\)個の箱すべてに玉が入る確率です。

2つのさいころが\(\,1\,\)と\(\,6\,\)の目が出たときなので、
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
&\,1\,&\,2\,&\,3\,&\,4\,&\,5\,&\,6\,\\ \hline
\,1\,& &　& & & & \color{red}{○}\\ \hline
2& &　& & & & \\ \hline
3& &　& & & & \\ \hline
4& & & & & & \\ \hline
5& & & & & & \\ \hline
6& \color{red}{○} & & & & & \\ \hline
\end{array}\)

　\(\displaystyle \frac{2}{36}=\underline{　\frac{1}{18}　}\)

(2)
\(\,4\,\)の箱に玉が入らない確率です。

2つの目が\(\,4\,\)をはさまなければ良いだけですね。

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
&\,1\,&\,2\,&\,3\,&\,4\,&\,5\,&\,6\,\\ \hline
\,1\,& \color{blue}{○} & \color{blue}{○}&\color{blue}{○} & × & × & ×\\ \hline
2& \color{blue}{○}& \color{blue}{○}& \color{blue}{○}& × & × & ×\\ \hline
3& \color{blue}{○}&\color{blue}{○}& \color{blue}{○} & × & × & ×\\ \hline
4& ×& × & × & × & × & ×\\ \hline
5& ×& × & × & × & \color{blue}{○} & \color{blue}{○}\\ \hline
6& ×& × & × & × & \color{blue}{○} & \color{blue}{○}\\ \hline
\end{array}\)

答え　 \(\displaystyle \underline{　\frac{13}{36}　}\)

3.関数総合問題

問題に与えられた条件を確認しておきます。

　関数\(\,y=ax^2\,\)上に\(\,2\,\)点\(\,\mathrm{A,B}\,\)がある。
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-3\,\)
　\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,6\,\)
　直線\(\,\mathrm{OB}\,\)の傾きは\(\,\displaystyle \frac{3}{2}\,\)

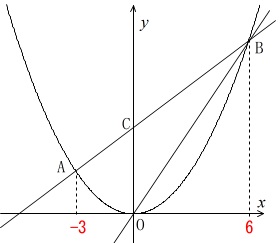
比例定数の決定

(1)
直線\(\,\mathrm{OB}\,\)の方程式は原点を通る直線で

　\(\displaystyle y=\frac{3}{2}x\)

点\(\,\mathrm{B}\,\)はこの直線上の点なので\(\,y\,\)座標は

　\(\begin{eqnarray}\displaystyle
y&=&\frac{3}{2}\times (6)\\
&=&9
\end{eqnarray}\)

放物線は点\(\,\mathrm{B}\,(\,6\,,\,9\,)\)を通るので

　\(\begin{eqnarray}\displaystyle
9&=&a\times (6)^2\\
a&=&\frac{9}{36}\\
&=&\underline{　\frac{1}{4}　}
\end{eqnarray}\)

直線の方程式

(2)
\(\,\mathrm{A}\,\)は放物線上の点なので\(\,y\,\)座標は

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{4}\times (-3)^2\\
&=&\frac{9}{4}
\end{eqnarray}\)

よって直線\(\,\mathrm{AB}\,\)は

　\(\,\displaystyle \left(\,-3\,,\,\frac{9}{4}\,\right)\,\)
　\(\hspace{4pt}(\hspace{6pt}\,6\,,\hspace{4pt}9\hspace{4pt})\,\)

の\(\,2\,\)点を通る直線で

　\(\begin{eqnarray}\displaystyle
(傾き)&=&\frac{　y\,の増加量　}{　x\,の増加量　}\\
&=&\frac{9-\frac{9}{4}}{6-(-3)}\\
&=&\frac{\frac{36-9}{4}}{9}\\
&=&\frac{27}{36}\\
&=&\frac{3}{4}
\end{eqnarray}\)

切片\(\,\mathrm{C}\,\)を\(\,b\,\)とおいて

　\(\displaystyle y=\frac{3}{4}x+b\)

この直線は\(\,\mathrm{B}\,\)\(\,(\,6\,,\,9\,)\,\)を通るので

　\(\begin{eqnarray}\displaystyle
9&=&\frac{3}{4}\times (6)+b\\
b&=&9-\frac{9}{2}\\
&=&\frac{9}{2}
\end{eqnarray}\)

よって、求める直線\(\,\mathrm{AB}\,\)の方程式は

　\(\displaystyle \underline{　y=\frac{3}{4}x+\frac{9}{2}　}\)

しまった。こんなに丁寧に説明する問題ではなかった。笑

面積を等しくする座標決定問題

(3)
\(\,x\,\)軸上に\(\,x\,\)座標が正となる点\(\,\mathrm{D}\,\)をとって、
\(\,\mathrm{D}\,\)を通り、傾きが\(\,\displaystyle \frac{6}{25}\,\)である直線の切片を\(\,\mathrm{E}\,\)として、
\(\,\mathrm{△OCA=△OED}\,\)となる点\(\,\mathrm{D\,,\,E}\,\)を求めます。

あれこれ考えたいですが、切片\(\,\mathrm{E}\,\)の\(\,y\,\)座標を\(\,k\,\)とおいて、
\(\,\mathrm{△OCA=△OED}\,\)を方程式にしましょう。

直線\(\,\mathrm{DE}\,\)を
　\(\displaystyle y=\frac{6}{25}x+k\)
とすると、\(\,\mathrm{D}\,\)は\(\,y=0\,\)のときなので、

　\(\begin{eqnarray}\displaystyle
0&=&\frac{6}{25}x+k\\
&=&6x+25\,k\\
6x&=&-25\,k\\
x&=&-\frac{25}{6}\,k
\end{eqnarray}\)

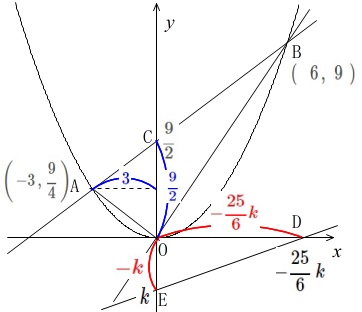
\(\,k\,\)そのものは負の数です。

\(\,\mathrm{△OCA=△OED}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{△OCA}&=&\mathrm{△OED}\\
\frac{1}{2}\times \frac{9}{2}\times 3&=&\frac{1}{2}\times (-k)\times \left(-\frac{25}{6}k\right)\\
81&=&25\,k^2\\
k^2&=&\frac{81}{25}\\
k&=&-\frac{9}{5}　(\,k\,＜\,0)
\end{eqnarray}\)

このとき

　\(\hspace{10pt}\displaystyle -\frac{25}{6}k\\
\displaystyle =-\frac{25}{6}\times \left(-\frac{9}{5}\right)\\
\displaystyle =\frac{15}{2}\)

よって、

　\(\,\mathrm{\underline{　D\,\left(\,\displaystyle \frac{15}{2}\,,\,0\,\right)　}}\,\)

　\(\,\mathrm{\underline{　E\,\left(\,\displaystyle 0\,,\,-\frac{9}{5}\,\right)　}}\,\)

前半\(\,1\,\)から\(\,3\,\)まではここまでです。

⇒　2019年京都府公立高校(前期)入試の数学問題の解説【後半】

後半は空間図形、平面図形、そして、規則性の応用問題です。

前半の方が問題数は多くほんの少しだけ配点も多くありますが、後半は前半以上に時間がかかるので合否を分けるのは後半でしょう。

⇒　京都府公立高校入試数学の過去問と解答解説

\(\,\large{6}\,\)の規則性問題は\(\,2018\,\)年の京都府前期問題ほどではありませんが、
全体を通してガンガン手を動かして処理しないと高得点は取りにくいですね。