長方形の周と縦と横の長さの関係問題の解き方 1次方程式(中1)

周の長さと縦と横の長さの関係についての問題を方程式を利用して解く方法です。
面積と長さの関係は2次方程式が多いですがここでは中学1年の時点で解ける1次方程式を利用する解き方です。
1次方程式を利用するかどうかよりももっと重要な点がありますので確認しておきましょう。

長方形の問題で大切なポイント

長方形に限ったことではありませんが、
「長方形」って問題にあって図を書かないというのははっきり言って解く気がない人ですね。
また、図を書くように指導していない人は、指導経験がない人です。
しかしそんな指導者はいないはずなので必ず言われているはずなのに、書かない人がいますが、天才ですか？笑

相当経験を積んだ人ならイメージだけで方程式を立てることができるでしょうが、
１次方程式をやっている頃はそれほど経験はないはずです。

図を書きましょう。
問題がイメージできるだけじゃなくて、問題が簡単になりますから。

１次方程式を立てることなんてものすごく簡単に思えてきますよ。

縦と横の長さ関係を1次方程式にする

問題を見ながら説明します。

図を書けばすぐに方程式が立てられます。
縦が横より \(\,5\,\) cm長い長方形です。

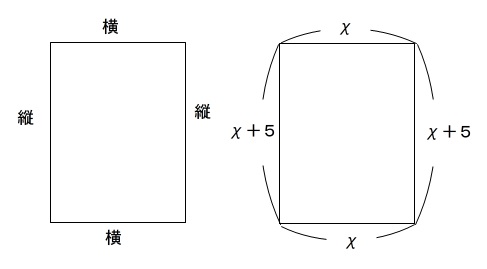
周の長さは横が\(\,2\,\)つ、縦が\(\,2\,\)つ分あることに注意して、
求めたい横の長さを \(\color{red}{x}\) としましょう。
すると縦の長さは横の長さより \(\,5\,\) cm長いので \(\color{red}{(x+5)}\) とおけます。

すべての辺を足すと \(\,50\,\) cmと問題にあるので、

　\(x\times 2+(x+5)\times 2=50\)

という方程式が立ちます。
後はこれを解くだけです。

　\(\begin{eqnarray}
2x+2(x+5)&=&50\\
2x+2x+10&=&50\\
4x&=&50-10\\
4x&=&40\\
x&=&10
\end{eqnarray}\)

この \(x\) が横の長さで、問題の求めているのもと一緒なので、答えです。

　（答え）\(\,\underline{　10 \,\mathrm{cm}　}\,\,\)

縦の長さを \(x\) とした場合、横の長さは \((x-5)\) なので間違えないようにすることと、
答えは横の長さなので、\(x\) そのものは答えではなくなることに注意しましょう。

長方形の縦と横の比がわかるときの方程式

何から始めるか？
図を書くことから始めます。

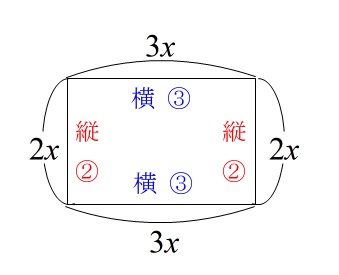
縦を求めたいので縦の長さを \(x\) としてもいいのですが、

　\(\color{red}{(縦の長さ)：(横の長さ)=2：3}\)

なので、
横の長さが分数になるので直接は求まりませんが縦の長さを \(2x\) とおきました。
すると横の長さは \(3x\) となります。

　\((縦の長さ)：(横の長さ)=2x：3x=2:3\)

となるので問題ないことがわかるでしょう。

答えるときに気をつけておけば計算しやすい文字の使い方をすればいいですよ。

関係式は周の長さが \(50\) cmであることで、
縦と横が\(\,2\,\)つずつあることに注意して、

　\(2\times 2x+2\times 3x=50\)

これを解いて

　\(\begin{eqnarray}
4x+6x&=&50\\
10x&=&50\\
x&=&5
\end{eqnarray}\)

これが答えではありません。

求めたいのは縦の長さなので、
　\(2x=2\times 5=10\) cmです。

　（答え）\(\underline{\,10\,(\mathrm{cm})\,}\)

答えの確認は元の図に戻して見ればすぐにできます。
縦が \(\,10\,\) cm、横が \(\,15\,\) cm、これが二組で長方形なので、
\(2\times (10+15)=50\) cmになっています。

方程式の問題は道のりなどの問題もありますが、図（線分図）を書いて考えれば同じです。
峠や山が出てきて登ったり下ったりするときも線分でいいですよ。
実感しやすい、わかりやすいなら折れ線にしてもいいですけど、いらないでしょう。笑

長方形の問題は2次方程式（中学3年）でやり直すことになるでしょう。
そのとき何が大事かって、図を書いて考えると言うことです。
2次方程式なんて誰でも解けるようになりますが、図を書くということをしない人はそれ以前に図形分野で数学を苦手にしているので、数学の問題への取り組み方への土台が違っていますから注意しておくと良いです。

1次方程式は立式できれば解くのは簡単です。

⇒　方程式とは？方程式の解と移項とは？基本問題の解き方(中１数学)

基本的な計算から少し復習しておけばいいです。
ただ、１次方程式が解けないなら連立方程式は解けませんので確実に解けるようにしておきましょう。

ここでは比例式の計算練習は取り上げていませんが、

⇒　比例式(分数,小数,(かっこ)のついた問題)の解き方

簡単なので確認しておいてください。

⇒　1次方程式と比例式の利用と解き方のまとめ

三年生の相似では比例式が解けないと答えは出てこないものがほとんどです。

クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！

その悩み、『覚え太郎』が解決します！！！