食塩水の濃度の求め方と濃度の違う溶液を混ぜる問題を1次方程式で考えるときのポイントです。
連立方程式でも食塩の問題は出てきますが、ここでは中学１年の範囲で説明します。
食塩の濃度や混合の問題では何に注目して方程式を立てるかが大切になりますので確認しておきましょう。
食塩水の濃度の求め方
文章題の中でも、みんなが１番苦手とする食塩水（濃度）の問題です。
濃度の計算は理科でも出てきますが、ここでも説明しておきます。
例えば、「食塩水」というのは、「食塩」と「水」が混じったものです。
食塩は溶けているもの、水は溶かしているものです。
この溶けているものを「溶質(ようしつ)」、溶かしているものを「溶媒(ようばい)」と言います。
そして、混じった食塩水のことを「溶液(ようえき)」と言います。
つまり、
\(\large{\color{red}{「溶液」}＝\color{blue}{「溶質」}＋\color{green}{「溶媒」}}\)
です。
※
溶媒はいろいろな物質がありますが、中学生は水だけ考えておけばいいですよ。
「食塩水の濃度」は質量パーセント濃度のことです。
\(\displaystyle \large{（濃度）＝\frac{\color{blue}{（溶質）}}{\color{red}{（溶液）}}\times 100}（％）\)
溶液は（溶質）＋（溶媒）なので、
\(\displaystyle （濃度）＝\frac{（\color{blue}{溶質}）}{（\color{green}{溶媒}）＋（\color{blue}{溶質}）}\times 100（％）\)
と表すこともできます。
\(\,5\,\)％の食塩水というのは、\(\,100\,\)ｇの食塩水中に\(\,5\,\)ｇの食塩が溶けています。
\(\,8\,\)％の食塩水というのは、\(\,100\,\)ｇの食塩水中に\(\,8\,\)ｇの食塩が溶けています。
このように溶液\(\,100\,\)ｇ中の食塩の量を出しておくと考えやすいです。
『基準』という意味では、
「\(\,1\,\)ｇの食塩水中に\(\,0.05\,\)ｇの食塩」
などとすると式は立てやすいですが、
\(\,100\,\)ｇ中の食塩の量を考えた方が楽になる場合が多いです。
間違えないでください。
普通に濃度といっている質量パーセント濃度とは、
\(\,100\,\)ｇの水に溶けている溶質の質量ではありません。
溶液\(\,100\,\)ｇ中の溶質の質量ですよ。
※
水\(\,100\,\)ｇにとける溶質の量は、飽和溶液の「溶解度」で出てくる数字なので間違えないように注意してください。
食塩水を混ぜる問題を考えるときのポイント
食塩水の濃度に関係するのは「食塩水」「食塩」「水」の３つです。
関係式を作るとき、つまり方程式を立てるときは、
「食塩に注目して立式する」
を基本にしておくといいです。
求めるものが「加える水」であっても立式に利用するのは食塩を追いかけるということです。
食塩水で立式してもいい場合はありますが、水で方程式を立てるというのは難しいですよ。
食塩水の問題を１次方程式で解く演習
食塩水を混ぜる問題を見ながら説明します。
\(\,5 \,\)％の食塩水 \(\,800\,\)ｇに\(\,8\,\) ％の食塩水を混ぜて\(\,6 \,\)％の食塩水を作りたい。
\(\,8\,\)％の食塩水を何ｇ混ぜればよいか求めなさい。
ここでは図を利用しましょう。
「分からないもの」、「求めたいもの」は文字でおくんですよね。
求めたいのは\(\,8\,\)％の食塩水の量なのでこれを \(x\) とおきましょう。
問題は、
「 \(\,5\,\)％の食塩水\(\,800\,\)ｇと\(\,8\,\)％の食塩水 \(x\) ｇを混ぜると\(\,6\,\)％になる」
となります。
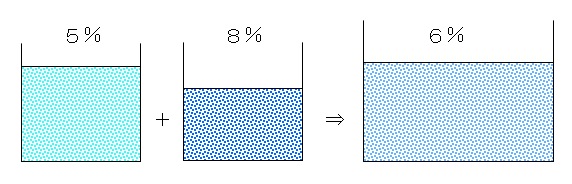
合わせると食塩水は全体で \((800+x)\) gになっています。
このとき「食塩」の関係が
｢\(\,5\,\) ％食塩水中の食塩｣＋｢\(\,8\,\) ％食塩水中の食塩」=｢\(\,6\,\) ％の食塩水中の食塩｣
となっていればいいわけです。
食塩の量は食塩水を混ぜても、減ったり増えたりしないからです。
ここでそれぞれの食塩水中の食塩を表します。
\(\,5\,\)％の食塩水\(\,100\,\)ｇ中には\(\,5\,\)ｇ入っていますので、
\(\,800\,\)ｇ中にはその\(\,8\,\)倍の食塩が入っています。
\(\,5\,\) ％の食塩水 \(\,800 \,\)ｇ中の食塩は
\(\displaystyle 5\times \frac{800}{100}(=40)\) (g) ･･･①
同じように、\(\,8 \,\)％の食塩水 \(x\) g中の食塩は
\(\displaystyle 8\times \frac{x}{100}\) (g) ･･･②
合わせた食塩水 \(\,6\,\) ％の \((800+x)\) g中には
\(\displaystyle 6\times \frac{800+x}{100}\) (g) ･･･③
この「食塩の量」を表せるかどうかで、解けるかどうかが決まります。
後は、\(①+②=③\) と方程式を立てればいいのです。
\(\displaystyle 5\times \frac{800}{100}+8\times \frac{x}{100}=6\times \frac{800+x}{100}\)
この方程式の分母 \(\,100\,\) は必要ありませんね。
両辺を \(\,100\,\) 倍して分母をなくします。
\(\begin{eqnarray}
5\times 800+8x&=&6(800+x)\\
4000+8x&=&4800+6x\\
8x-6x&=&4800-4000\\
2x&=&800\\
x&=&400
\end{eqnarray}\)
（答え）\(\underline{\,400\,(\mathrm{g})}\,\)
数字が大きくなることもありますが自信を持って方程式を処理してください。
確かめてみましょう。
5％の食塩水800ｇ中には \(\displaystyle 5\times \frac{800}{100}=40\) g
8％の食塩水400ｇ中には \(\displaystyle 8\times \frac{400}{100}=32\) g
6％の食塩水1200ｇ中には \(\displaystyle 6\times \frac{1200}{100}=72\) g
の食塩があるので確かに混ぜる前と後で一致しています。
濃度の問題に限らず文章題を文章だけで考えると分かりにくいので、図やグラフを利用するんです。
ここでは図に書き込んでいませんが、
それぞれの条件を図の中や下に書き込むともっとわかりやすくなりますよ。
いずれ連立方程式を解くことになりますが、同じことです。
⇒ 連立方程式(食塩水の濃度と食塩水を混ぜる文章問題の立式方法と解き方)
中１の1次方程式をやっている段階ではグラフはまだ登場していませんが、図やグラフを利用することは数学の解答上での基本です。
全部が直接解答に結びつくわけではありませんが、考えるときの手助けをしてくれことが多くなります。
めんどくさがらずに書いて下さいね。
数学の問題は、「式、図、グラフでセット」、と覚えておいて下さい。
高校でものすごい差となって出てきます。
それと、食塩水の水と食塩と食塩水の関係は比例です。
比例計算に強くなっておくと理科でも計算問題で大いに活躍してくれます。
次は長方形の周の長さや縦、横の長さの関係の問題を方程式で解いてみましょう。
面積は２次方程式でやることになるので長さだけに限ります。
⇒ 長方形の周と縦と横の長さの関係問題の解き方 1次方程式(中1)
長方形の問題は3年で2次方程式取り入れられるので、1次方程式の問題は食塩水の混合よりは簡単です。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
