2019年京都府公立高校(前期)入試の数学問題の解説【後半】

2019年(平成31年度)に京都府で行われた公立高校入試の前期数学問題の解説の後半です。
ここでは第4問から第6問までを解説しますが、共通して言えるのは単純な公式利用問題は少ないということです。
決して難問と言うことではありませんが、応用する力は必要です。

問題は京都府も公開してくれています。

⇒　2019京都府【前期】問題

\(\,2018\,\)年よりはマシですが、\(\,\large{6}\,\)の規則性の読み取りは慣れていないと満点は厳しいでしょう。

4.空間図形の総合問題

\(\,\large{4}\,\)は空間図形の問題です。

三角柱を切り取った三角錐の体積、線分の長さと三角形の面積、そして平面と点の距離の問題があります。

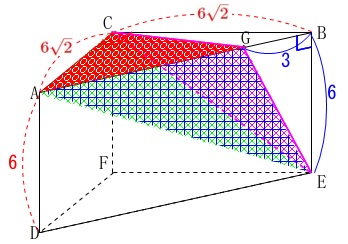
三角柱の条件を書き出し、図示しておきます。

条件

　\(\,\mathrm{AC=BC=6\sqrt{2}}\,\)
　\(\,\mathrm{AD=6}\,\)
　\(\,\mathrm{∠ACB=90^{\circ}}\,\)
　\(\,\mathrm{AG:GB=3:1}\,\)

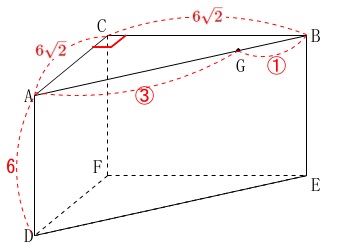
言うまでもないでしょうけど図は問題にありますが、数値を書き込んでいくのは自分です。

三角錐の体積

(1)三角錐\(\,\mathrm{ABCE}\,\)の体積です。

　底面は\(\,\mathrm{△ABC}\,\)
　高さは\(\,\mathrm{BE=AD}\,\)

または

　底面は\(\,\mathrm{△CBE}\,\)
　高さは\(\,\mathrm{AC}\,\)

となっています。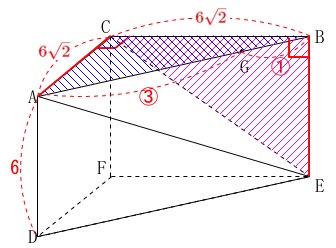

どちらも体積は同じです。

なので三角錐\(\,\mathrm{ABCE}\,\)の体積\(\,V\,\)は

　\(\begin{eqnarray}
V&=&\frac{1}{3}\times \frac{1}{2}\times (6\sqrt{2})^2\times 6\\
&=&\underline{　72　}　(\mathrm{cm^2})
\end{eqnarray}\)

高さがすぐに分からない三角形の面積

(2)は線分\(\,\mathrm{EG}\,\)の長さと\(\,\mathrm{△CEG}\,\)の面積を求めます。

\(\,\mathrm{EG}\,\)の長さは三平方の定理ですぐに求まりますが、
\(\,\mathrm{△CEG}\,\)は高さとなる垂線がありませんので補助線が必要になります。

\(\,\mathrm{△ABC}\,\)は直角三角形なので三角定規の比が使えます。
（三平方の定理でも同じです。）

　\(\begin{eqnarray}
\mathrm{AC:AB}&=&1:\sqrt{2}\\
6\sqrt{2}:\mathrm{AB}&=&1:\sqrt{2}\\
\mathrm{AB}&=&\color{red}{12}
\end{eqnarray}\)

\(\,\mathrm{AG:GB}=3:1\,\)なので

　\(\begin{eqnarray}
\mathrm{BG}&=&\frac{1}{4}\times 12\\
&=&\color{blue}{3}
\end{eqnarray}\)
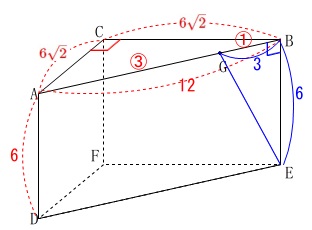直角三角形\(\,\mathrm{EBG}\,\)に三平方の定理を用いて、

　\(\begin{eqnarray}
\mathrm{EG^2}&=&\mathrm{GB^2+EB^2}\\
&=&3^2+6^2\\
&=&45\\
\mathrm{EG}&=&\underline{　3\sqrt{5}　}　(\,\mathrm{EG}\,＞\,0\,)
\end{eqnarray}\)

次に\(\,\mathrm{△CEG}\,\)の面積です。

\(\,\mathrm{EG}\,\)は求めましたが、底辺と高さが決められません。

\(\,\mathrm{CE}\,\)は長方形\(\,\mathrm{BCFE}\,\)の対角線なので

　\(\begin{eqnarray}
\mathrm{CE^2}&=&\mathrm{BC^2+BE^2}\\
&=&(6\sqrt{2})^2+6^2\\
&=&72+36\\
&=&108\\
\mathrm{CE}&=&\color{magenta}{6\sqrt{3}}　(\,\mathrm{CE}\,＞\,0\,)
\end{eqnarray}\)
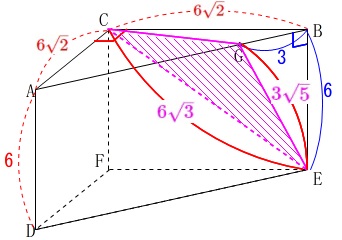ここで\(\,\mathrm{CG}\,\)の長さが欲しいところです。

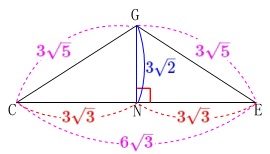
そこで\(\,\mathrm{△ABC}\,\)を抜き出します。
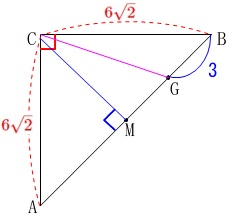\(\,\mathrm{AB}\,\)の中点を\(\,\mathrm{M}\,\)とすると、
\(\,\mathrm{△BMC}\,\)も\(\,\mathrm{△AMC}\,\)も直角二等辺三角形で、

\(\,\mathrm{AB=12}\,\)なので、

　\(\mathrm{AM=BM=CM}=6\)

だから

　\(\mathrm{MG=BM-BG}=3\)
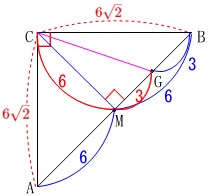\(\,\mathrm{△CMG}\,\)に三平方の定理を使って、

　\(\begin{eqnarray}
\mathrm{CG^2}&=&\mathrm{CM^2+MG^2}\\
&=&3^2+6^2\\
&=&9+36\\
&=&45\\
\mathrm{CG}&=&\color{magenta}{3\sqrt{5}}
\end{eqnarray}\)
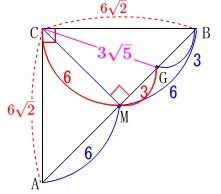このとき\(\,\mathrm{△CEG}\,\)は二等辺三角形になります。

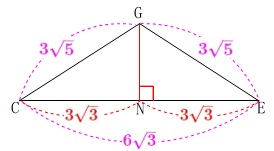頂角\(\,\mathrm{G}\,\)の二等分線は\(\,\mathrm{CE}\,\)を垂直に二等分するので、

　\(\begin{eqnarray}
\mathrm{GN^2+CN^2}&=&\mathrm{CG^2}\\
\mathrm{GN}^2+(3\sqrt{3})^2&=&(3\sqrt{5})^2\\
\mathrm{GN}^2&=&45-27\\
&=&18\\
\mathrm{GN}&=&\color{blue}{3\sqrt{2}}　(\,\mathrm{GN}\,＞\,0\,)
\end{eqnarray}\)
よって、

　\(\begin{eqnarray}\displaystyle
\mathrm{△CEG}&=&\frac{1}{2}\times \mathrm{CE}\times \mathrm{GN}\\
&=&\frac{1}{2}\times 6\sqrt{3}\times 3\sqrt{2}\\
&=&\underline{　9\sqrt{6}　}　(\mathrm{cm^2})
\end{eqnarray}\)

ちょっと丁寧にやりすぎですね。
すでに長くなってきました。笑

点と面との距離

平面の方程式が使えませんので、立体図形での高さとなる点と面との距離は体積を利用します。
錐体\(\,\mathrm{E-ACG}\,\)の体積\(\,V_2\,\)は、

　底面を\(\,\mathrm{△ACG}\,\)
　高さを\(\,\mathrm{CF=AD=6}\,\)

と見ることができて、\(\,\mathrm{AG:GB=3:1}\,\)から

　\(\begin{eqnarray}\displaystyle
\mathrm{△ACG}&=&\frac{3}{4}\times \mathrm{△ABC}\\
\end{eqnarray}\)

底面積が\(\,\displaystyle \frac{3}{4}\,\)倍で高さが同じなので

三角錐\(\,\mathrm{ABCE}\,\)の体積\(\,V\,\)が(1)から\(\,\color{red}{72}\,\)であることから

　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{3}{4}\times \color{red}{72}
&=&\color{blue}{54}
\end{eqnarray}\)

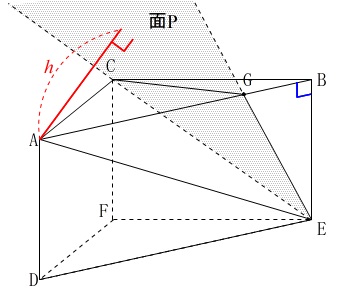
この錐体は
　\(\,\mathrm{△CEG}\,\)を底面
　\(\,\mathrm{A}\,\)と平面\(\,\mathrm{P}\,\)との距離\(\,\color{red}{h}\,\)を高さ
と見ることもでき、同じ立体なので当然体積は同じ\(\,\color{blue}{54}\,\)です。

　\(\mathrm{△CEG}=9\sqrt{6}\)

なので

　\(\begin{eqnarray}
\frac{1}{3}\times 9\sqrt{6}\times \color{red}{h}&=&\color{blue}{54}\\
3\sqrt{6}\,h&=&54\\
h&=&\frac{54}{3\sqrt{6}}\\
&=&\underline{　3\sqrt{6}　}　(\mathrm{cm})
\end{eqnarray}\)

面積と同じように立体を転がしても体積は変わらない、ということです。
　

5.平面図形の総合問題

問題の条件を図に書き込んで考えていきましょう。

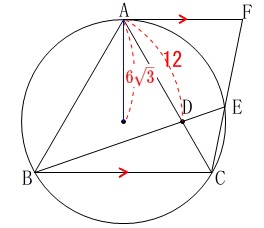
条件
　\(\,\mathrm{A,B,C,E}\,\)は円\(\,\mathrm{O}\,\)の周上の点
　円\(\,\mathrm{O}\,\)の半径\(\,\color{red}{6\sqrt{3}}\,\)
　\(\,\mathrm{△ABC}\,\)は正三角形
　\(\,\mathrm{AD=12}\,\)
　\(\,\mathrm{AF\, /\!/ \,BC}\,\)

合同の証明

(1)
\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△ACF}\,\)が合同であることを証明します。

円周上の点がいくつかあるので円周角が等しいものがあります。

それと、見落としてはいけないのは、

　　\(\,\mathrm{\color{red}{AF\, /\!/ \,BC}}\,\)

です。

何度も言うことになりますが、問題に必要無い条件はありません。

それから合同や相似を証明したいなら、図の中で証明を完成させてからです。

図の中で示せないことを文章にはできません。
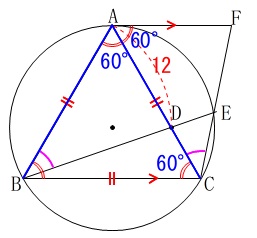\(\,\mathrm{△ABC}\,\)が正三角形であることから、

　\(\mathrm{AB=BC=CA}\)
　\(\mathrm{∠BAC=∠BCA}=60^{\circ}\)

\(\,\mathrm{\color{red}{AF\, /\!/ \,BC}}\,\)なので錯角が等しくなるので

　\(\,\mathrm{∠BCA=CAF=60^{\circ}}\,\)

また\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AB}}}\,\)の円周角から

　\(\,\mathrm{\color{magenta}{∠ABD=∠ACF}}\,\)

これで証明が終わっています。

（証明）

　\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△ACF}\,\)において

\(\,\mathrm{△ABC}\,\)は正三角形なので

　\(\,\mathrm{AB=AC}\,　･･･①\)

また\(\,\mathrm{AF\, /\!/ \,BC}\,\)であることから、
平行線の錯角は等しいので

　\(\,\mathrm{∠BAD=∠CAF=60^{\circ}}\,　･･･②\)

さらに同一弧の円周角は等しいので

　\(\,\mathrm{∠ABD=∠ACF}\,　･･･③\)

①②③より

　\(\,1\,\)辺とその両端の角がそれぞれ等しい

ので、

　\(\,\mathrm{△ABD}\,\)　≡　\(\,\mathrm{△ACF}\,\)
（終わり）

正三角形、平行線の条件を見逃すと証明はできません。

線分の長さの求め方

(2)
線分\(\,\mathrm{BD}\,\)の長さを求めますが、長さの条件が少ないので分かる長さをある程度出しておきましょう。

\(\,\mathrm{△ABC}\,\)が正三角形であることから、
直線\(\,\mathrm{AO}\,\)は\(\,\mathrm{∠BAC}\,\)の二等分線になります。

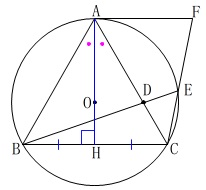
よって\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{H}\,\)とすると、
円の中心\(\,\mathrm{O}\,\)は\(\,\mathrm{△ABC}\,\)の重心であり、

　\(\,\mathrm{AO:OH=2:1}\,\)

なので

　\(\,\mathrm{OH=\color{red}{3\sqrt{3}}}\,\)

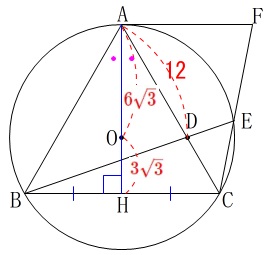このとき

　\(\,\mathrm{AH=\color{red}{9\sqrt{3}}}\,\)

\(\,\mathrm{△ABH}\,\)は三角定規なので

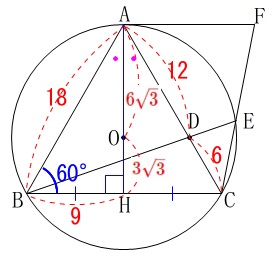
　\(\,\mathrm{BH=9}\,\)
　\(\,\mathrm{AB=AC=18}\,\)
から
　\(\,\mathrm{DC=6}\,\)

ここで(1)で証明した合同を利用したいのでですが、
\(\,\mathrm{D}\,\)から\(\,\mathrm{BC}\,\)に垂線を\(\,\mathrm{DI}\,\)下ろすと、
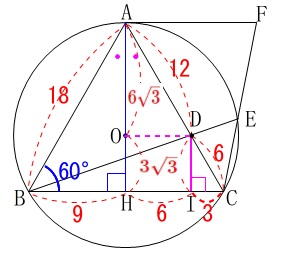\(\,\mathrm{△DCI}\,\)が三角定規で、

　\(\,\mathrm{CI=3}\,\)
　\(\,\mathrm{DI=3\sqrt{3}}\,\)

となるので、

　\(\,\mathrm{BI=9+6=15}\,\)

直角三角形\(\,\mathrm{BID}\,\)に三平方の定理を利用すると、

　\(\begin{eqnarray}
\mathrm{BD^2}&=&\mathrm{BI^2+DI^2}\\
&=&15^2+(3\sqrt{3})^2\\
&=&225+27\\
&=&252
\end{eqnarray}\)

\(\,\mathrm{BD\,＞\,0}\,\)より

　\(\mathrm{BD}=\underline{　6\sqrt{7}　}　(\mathrm{cm})\)

四角形と三角形の面積比

(3)
四角形と三角形の面積比を求めます。

具体的に面積を求めても良いのですが、相似を使いましょう。

長くなっているので一気にいきます。
決してめんどくさくなったわけではありません。笑
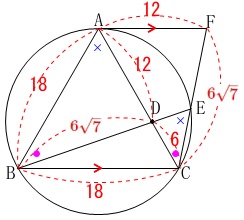(1)から\(\,\mathrm{△ABD}\,\)　≡　\(\,\mathrm{△ACF}\,\)なので、

　\(\,\mathrm{CF}=6\sqrt{7}\,\)

また\(\,\mathrm{△ABD}\,\)　∽　\(\,\mathrm{△ECD}\,\)なので

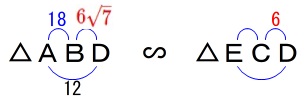
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:EC}&=&\mathrm{DB:DC}\\
\color{blue}{18}:\mathrm{EC}&=&\color{red}{6\sqrt{7}}:\color{red}{6}\\
6\sqrt{7}\times \mathrm{EC}&=&18\times 6\\
\mathrm{EC}&=&\frac{18\times 6}{6\sqrt{7}}\\
&=&\frac{18\sqrt{7}}{7}
\end{eqnarray}\)

このとき

　\(\begin{eqnarray}\displaystyle
\mathrm{EF}&=&\mathrm{CF-CE}\\
&=&6\sqrt{7}-\frac{18\sqrt{7}}{7}\\
&=&\frac{42\sqrt{7}-18\sqrt{7}}{7}
&=&\frac{24\sqrt{7}}{7}
\end{eqnarray}\)

よって

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{CE:EF}}&=&\frac{18\sqrt{7}}{7}:\frac{24\sqrt{7}}{7}\\
&=&\color{blue}{3:4}
\end{eqnarray}\)

さて、なんでこの比を出したかというと、
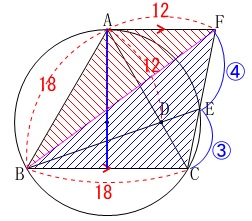いきなり四角形\(\,\mathrm{ABEF}\,\)と\(\,\mathrm{△BCE}\,\)の比較は難しいと判断したので、
　\(\,\mathrm{\color{red}{△ABF}}\,\)と\(\,\mathrm{\color{blue}{△BEF}}\,\)と\(\,\mathrm{\color{blue}{△ACE}}\,\)
3つの三角形に分けようと考えたからです。

そこで、先に辺の比を出しておきました。

では面積比を出しましょう。

\(\,\mathrm{△ABF}\,\)と\(\,\mathrm{△BCF}\,\)は高さが同じなので底辺の比が面積比になります。

　\(\begin{eqnarray}
\mathrm{△ABF}:\mathrm{△BCF}&=&\mathrm{AF:BC}\\
&=&12:18\\
&=&\color{red}{2:3}
\end{eqnarray}\)

また、\(\,\mathrm{△BEF}\,\)と\(\,\mathrm{△BCE}\,\)は高さが同じなので底辺の比が面積比になります。

　\(\begin{eqnarray}
\mathrm{△BEF}:\mathrm{△BCE}&=&\mathrm{EF:CE}\\
&=&\color{blue}{4:3}
\end{eqnarray}\)
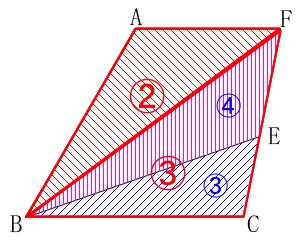\(\,\mathrm{△BCF}\,\)の\(\,\color{blue}{⑦}\,\)と\(\,\color{red}{③}\,\)の最小公倍数（公倍数なら何でも良いです）をとって、

　\(\,\mathrm{△BCF=}\,\color{magenta}{\fbox{\(\,\color{magenta}{21}\,\)}}\)

とすると、

　\(\begin{eqnarray}\displaystyle
\mathrm{△ABF}&=&\frac{2}{3}\times \color{magenta}{\fbox{\(\,\color{magenta}{21}\,\)}}\\
&=&\color{magenta}{\fbox{\(\,\color{magenta}{14}\,\)}}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
\mathrm{△BEF}&=&\frac{4}{7}\times \color{magenta}{\fbox{\(\,\color{magenta}{21}\,\)}}\\
&=&\color{magenta}{\fbox{\(\,\color{magenta}{12}\,\)}}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
\mathrm{△BCE}&=&\frac{3}{7}\times \color{magenta}{\fbox{\(\,\color{magenta}{21}\,\)}}\\
&=&\color{magenta}{\fbox{\(\,\color{magenta}{9}\,\)}}
\end{eqnarray}\)
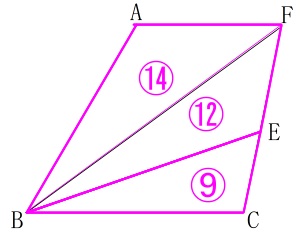よって

　\(\hspace{10pt}\mathrm{(四角形ABEF):△BCE}\\
=(\mathrm{△ABE+△AEF}):\mathrm{△BCE}\\
=(14+12):9\\
=\underline{　26:9　}
\)

6.規則性の応用

\(\,\large{6}\,\)は規則性の問題です。

〈操作〉と書いてある方法がルールです。

　\(\,1\,\)から\(\,m\,\)までの自然数が書かれたカードが下に行くほど大きくなるように重ねてある。
　上から\(\,2\,\)番目のカードを一番下に移動させ、一番上のカードは取り除く。

簡単に言うと、

　上から\(\,1,2,3,\cdots\,,m\,\)の順に重ねてあり、
　\(\,1\,\)番上のカードを取り、\(\,2\,\)番目を\(\,1\,\)番下に回すことを繰り返す、

ということです。

　\(\,m\,\)は\(\,3\,\)以上の自然数

というのは考えなくて良いように問題が設定されています。

ルールになれるために練習問題を用意してくれていますので、実際にやってみましょう。

(1)
\(\,m=8\,\)のとき、つまり最初\(\,8\,\)枚あって、残りが\(\,4\,\)枚になるまで繰り返します。

このときに気がつかなければならないのは、

　\(\,1\,\)回の操作で減るカードは\(\,1\,\)枚だけ

ということです。

\(\,8\,\)枚のカードを残り\(\,4\,\)枚まで繰り返すということは、
\(\,4\,\)回操作を行うと言うことです。

\(\,4\,\)回くらいの操作は時間はかからないから実際にやってみて、という練習です。

\(\,Ⅱ図\,\)で\(\,m=7\,\)で残り\(\,3\,\)枚までの操作が書いてあります。
同じようにやれば良いだけですよ。

ここでは左から上にある数字を表しています。
赤の数字は次の〈操作〉で取り除かれる数字。
青の数字は次の〈操作〉で下にまわる数字です。

　\(\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline
　最初　 & \color{red}{1} & \color{blue}{2} & 3 & 4 & 5 & 6 & 7 & 8\\ \hline
　1回目の後　 & \color{red}{3} & \color{blue}{4} & 5 & 6 & 7 & 8 & 2 & \\ \hline
　2回目の後　 & \color{red}{5} & \color{blue}{6} & 7 & 8 & 2 & 4 & & \\ \hline
　3回目の後　 & \color{red}{7} & \color{blue}{8} & 2 & 4 & 6 & & & \\ \hline
　4回目の後　 & \color{magenta}{2} & 4 & 6 & \color{magenta}{8} & & & &\\ \hline
\end{array}\)

（答え）
　一番上　\(\,\underline{　2　}\,\)
　一番下　\(\,\underline{　8　}\,\)　

(2)
(1)の練習で気がついて欲しいのは、

　一回の操作で奇数が\(\,1\,\)から小さい順に1つずつ消えていく

ということです。

\(\,m=31\,\)、つまり\(\,1\,\)から\(\,31\,\)までの自然数があって、
残ったカードが\(\,16\,\)枚になるまで〈操作〉を繰り返すので、

　〈操作〉を\(\,15\,\)回行う

ということになります。

\(\,1\,\)から\(\,31\,\)までの自然数には\(\,16\,\)個の奇数があるので、
操作を\(\,15\,\)回行うと奇数が\(\,15\,\)個なくなっています。

並んでいる枚数は変わっていますが上からと下からの\(\,3\,\)枚だけを並べると

　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
　操作前　& 1 & 2 & 3 & \cdots & 29 & 30 & 31 \\ \hline
　1回後　& 3 & 4 & 5 & \cdots & 30 & 31 & 2 \\ \hline
　2回後　& 5 & 6 & 7 & \cdots & 31 & 2 & 4 \\ \hline
　\cdot　& \cdot & \cdot & \cdot & \cdots & \cdot & \cdot & \cdot \\ \hline
　\cdot　& \cdot & \cdot & \cdot & \cdots & \cdot & \cdot & \cdot \\ \hline
　14回後　& 29 & 30 & 31 & \cdots & 24 & 26 & 28 \\ \hline
　15回後　& \color{magenta}{31} & 2 & 4 & \cdots & 26 & 28 & \color{magenta}{30} \\ \hline
\end{array}\)

（答え）

　一番上　\(\,\underline{　31　}\,\)
　一番下　\(\,\underline{　30　}\,\)

(3)
\(\,m=294\,\)において、残りが\(\,73\,\)枚になるまで〈操作〉を繰り返します。

〈操作〉の回数は　\(294-73=221\)　回です。

同じように\(\,294\,\)個の自然数を並べて、
奇数を抜いていきますが、

　\(\,294\,\)までの自然数に奇数は\(\,147\,\)個

なので\(\,148\,\)回目からは奇数を抜き取るわけではありません。

\(\,147\,\)回までは奇数を抜き出し、\(\,148\,\)回目からは、

偶数のうち、\(\,2\times (奇数)\,\)を抜き取ります。

どういうことかというと、\(\,147\,\)回で奇数を全部抜き出した状態では、

　\(\,2,4,6,8,\,\cdots \,,\,290,292,294\,\)

が残っています。
この偶数を表し方を変えると、

　\(2\times 1\,,\,2\times 2\,,\,2\times 3\,,\,2\times 4\\
\cdots\\
2\times 145\,,\,2\times 146\,,\,2\times 147\)

の\(\,147\,\)個の偶数が並んでいます。

この後\(\,74\,\)回の〈操作〉を行いますが、
次に取り除く数字は、奇数番目の偶数です。

しかし、\(\,294=2\times 147\,\)なので偶数は\(\,147\,\)個ありますが、

　\(2\times (奇数)\)は\(\,74\,\)個

なので

　\(\,294\,\)を取り除くのが\(\,221\,\)回目

となります。

上から\(\,3\,\)枚、下から\(\,3\,\)枚を並べてみると、
　\(\,221\,\)回目には\(\,\color{red}{294}\,\)を取り除き、
　\(\,\color{blue}{4}\,\)を下に移動させるので

　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
　操作前　& 1 & 2 & 3 & \cdots & 292 & 293 & 294\\ \hline
　\cdot　& \cdot & \cdot & \cdot & \cdots & \cdot & \cdot & \cdot \\ \hline
　147回後　& 2 & 4 & 6 & \cdots & 290 & 292 & 294\\ \hline
　148回後　& 6 & 8 & 10 & \cdots & 292 & 294 & 4\\ \hline
　\cdot　& \cdot & \cdot & \cdot & \cdots & \cdot & \cdot & \cdot \\ \hline
　\cdot　& \cdot & \cdot & \cdot & \cdots & \cdot & \cdot & \cdot \\ \hline
　219回後　& 290 & 292 & 294 & \cdots & 280 & 284 & 288\\ \hline
　220回後　& \color{red}{294} & \color{blue}{4} & 8 & \cdots & 284 & 288 & 292\\ \hline
　221回後　& \color{magenta}{8} & 12 & 16 & \cdots & 288 & 292 & \color{magenta}{4}\\ \hline
\end{array}\)

（答え）
　一番上　\(\,\underline{　8　}\,\)
　一番下　\(\,\underline{　4　}\,\)

ながめているだけでは分からないでしょう。
自分で手を動かして、数字の動きを確認してみて下さい。

\(\,2019\,\)年京都府前期の問題は以上です。

⇒　2019年京都府公立高校(前期)入試の数学問題の解説

前半と配点はそれほど変わりませんが、やっている内容は倍以上です。
\(\,\large{6}\,\)で説明を簡単にしかしていませんが、作業量はかなりありますよ。

時間配分を考えて、手を止めないようにすることです。

⇒　京都府公立高校入試数学の過去問と解答解説

\(\,2018\,\)年の規則性と見比べてみると分かりますが、少し簡単（作業的に楽）になっています。