2019年(平成31年度)大阪府公立高校入試の数学B問題の解説

2019年(平成31年度)に大阪府で行われた公立高校入試の数学B問題の解説です。
中学であつかう数学の基本を幅広く、少し応用した問題がそろっていますが、
分野や単元ごとにムラのない基本を身につけている人に取ってはそれほど時間のかかる問題はありません。

問題は大阪府で公開してくれています。

⇒　2019年大阪B問題

応用された問題や計算力を問う問題は多くないのでちゃちゃっと済ませましょう。

1.小問集合

\(\,1\,\)は(1)から(9)まであります。

数と式の計算

(1)
　\(\hspace{10pt}4^2\color{red}{-}(\color{blue}{-}6)\div 2\\
=16+3\\
=\underline{　19　}\)

符号の（－）と引き算の（－）を見分けましょう。

かけ算割り算が先で、足し算引き算が後です。

(2)
　\(\hspace{10pt}2(5a-3b)-7(a-2b)\\
=10a-6b-7a+14b\\
=\underline{　3a+8b　}\)

（かっこ）を外すときが一番ミスしやすいので、
\(\,2\,\)行目は飛ばさない方が良いです。

(3)
　\(\hspace{10pt}18xy^3\div (-3y)^2\\
=18xy^3\div 9y^2\\
\displaystyle =\frac{18xy^3}{9y^2}\\
=\underline{　2xy　}\)

割り算は逆数のかけ算にするとすべての文字式計算が楽になります。
が、ここでは必要ありませんね。
\(\,3\,\)行目は省略しても良いでしょう。

(4)
　\(\hspace{10pt}(\sqrt{7}+2\sqrt{5})(\sqrt{7}-2\sqrt{5})\\
=(\sqrt{7})^2-(2\sqrt{5})^2\\
=7-20\\
=\underline{　-13　}\)

公式　
　\(\color{red}{(a+b)(a-b)=a^2-b^2}\)
を利用しました。

見た瞬間に気がつかなければ、地道に展開しても良いですよ。
展開だけなのでその方がはやいです。

　\(\hspace{10pt}(\sqrt{7}+2\sqrt{5})(\sqrt{7}-2\sqrt{5})\\
=(\sqrt{7})^2-2\sqrt{35}+2\sqrt{35}-(2\sqrt{5})^2\\
=7-20\\
=\underline{　-13　}\)

度数分布表の最頻値と整数の性質

(5)
最頻値は一番度数の多い値のことです。

ただし、度数分布表では「階級値」をその階級の値と見なします。

度数が一番多いのは
　\(\,110\,\mathrm{g}\,\)以上\(\,120\,\mathrm{g}\,\)未満の階級
なので最頻値はこの階級値で
　
　\(\,\underline{　115\,\mathrm{g}　}\,\)

(6)
\(\,a,b\,\)ともに負の数のとき、つねに負になる式を選びます。

「つねに」成り立つということは、具体的な数値でも成り立たなければおかしいので、適当に\(\,a,b\,\)を決めてやればすぐに答えは出てきます。

　\(a=-1\,,\,b=-2\,\)のとき、

　ア　\(ab=(-1)\times (-2)=2\)
　イ　\(\color{red}{a+b}=(-1)+(-2)=\color{red}{-3}\)
　ウ　\(-(\color{red}{a+b})=-(\color{red}{-3})=3\)
　エ　\((a-b)^2=\{-3-(-2)\}^2=(-1)^2=1\)

負になるのは\(\,a+b\,\)で、

（答え）　\(\,\underline{　イ　}\,\)

「つねに」というときは、具体的に選んだ数字で成り立たない場合が1つでもあればダメです。

方程式と確率

(7)
正方形の長さを変えた長方形の面積の方程式を立てれば良いだけです。

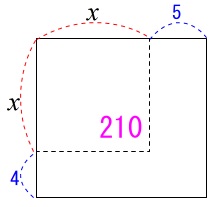
\(\begin{eqnarray}
(x+4)(x+5)&=&210\\
x^2+9x+20&=&210\\
x^2+9x-190&=&0\\
(x-10)(x+19)&=&0\\
x&=&10\,,\,-19
\end{eqnarray}\)

\(\,x\,\)は長さなので\(\,x\,＞\,0\,\)だから

　\(x=\underline{　10　}\)

(8)
\(\,\mathrm{A}\,\)の箱には　\(\,2,4,6\,\)
\(\,\mathrm{B}\,\)の箱には　\(\,1,3,5,7,9\,\)

のカードが1枚ずつ入っています。

\(\,\mathrm{A,B}\,\)から\(\,1\,\)枚ずつ取り出して、

　大きい方の数字を\(\,a\,\)

とするとき\(\,\color{red}{a}\,\)が\(\,3\,\)の倍数になる確率です。

樹形図ですぐに終わります。
ここでは表にしておきます。

　赤字が\(\,\mathrm{A}\,\)から取り出した数字
　青字が\(\,\mathrm{B}\,\)から取り出した数字
　大きい方の数字を中の数字で表します。

とします。

　\(\begin{array}{|c|c|c|c|c|c|} \hline
&　\color{blue}{1}　&　\color{blue}{3}　&　\color{blue}{5}　&　\color{blue}{7}　&　\color{blue}{9}　\\ \hline
　\color{red}{2}　& 2 & \color{magenta}{3} & 5 & 7 & \color{magenta}{9}\\ \hline
　\color{red}{4}　& 4 & 4 & 5 & 7 & \color{magenta}{9}\\ \hline
　\color{red}{6}　& \color{magenta}{6} & \color{magenta}{6} & \color{magenta}{6} & 7 & \color{magenta}{9}\\ \hline
\end{array}\)

よって\(\,a\,\)が\(\,3\,\)の倍数になる確率は

　\(\displaystyle \underline{　\frac{7}{9}　}\)

2点を通る直線の切片の求めかた

(9)
　\(\,m:y=x^2\,\)
　\(\displaystyle \,n:y=\frac{1}{4}x^2\)

\(\,\mathrm{A}\,\)は\(\,m\,\)上の点で\(\,x\,\)座標が\(\,2\,\)なので

　\(\,y=(2)^2=4\,\)

だから　\(\color{red}{\mathrm{A}\,(\,2\,,\,4\,)}\)

\(\,\mathrm{A}\,\)は\(\,n\,\)上の点で\(\,x\,\)座標が\(\,-3\,\)なので

　\(\displaystyle y=\frac{1}{4}(-3)^2=\frac{9}{4}\)

だから　\(\displaystyle \color{blue}{\mathrm{B}\,\left(\,-3\,,\,\frac{9}{4}\,\right)}\)

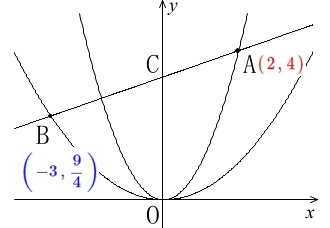
\(\ell\,\)は\(\,2\,\)点\(\,\mathrm{A,B}\,\)を通る直線で、

　\(\displaystyle \left(\,-3\,,\,\frac{9}{4}\,\right)\)
　\(\,(\hspace{10pt}2\,,\hspace{4pt}4\hspace{6pt})\,\)

から傾きが

　\(\hspace{10pt}\displaystyle \frac{4-\frac{9}{4}}{2-(-3)}\\
\displaystyle =\frac{\frac{7}{4}}{5}\\
\displaystyle =\frac{7}{20}\)

このとき\(\,\ell\,\)は

　\(\displaystyle y=\frac{7}{20}x+b\)

とおけて、この切片\(\,b\,\)が求める\(\,\mathrm{C}\,\)の\(\,y\,\)座標です。

この直線は\(\,\mathrm{A\,(2,\,4\,)}\,\)を通るので、

　\(\begin{eqnarray}\displaystyle
4&=&\frac{7}{20}\times (2)+b\\
4&=&\frac{7}{10}+b\\
b&=&4-\frac{7}{10}\\
&=&\frac{40-7}{10}\\
&=&\underline{　\frac{33}{10}　}
\end{eqnarray}\)

\(\,\large{1}\,\)は以上です。

2.規則性から導く1次関数と1次方程式

パイプ椅子を\(\,1\,\)直線上に\(\,1\,\)列に並べる問題ですが、
パイプ椅子で無くても線分でも同じです。

　パイプ椅子\(\,1\,\)個だと\(\,40\,\)の長さ
　パイプ椅子が\(\,1\,\)個増えると\(\,\mathrm{OP}\,\)は\(\,90\,\)増える

というのが条件です。
（単位は\(\,\mathrm{cm}\,\)ですが省略します。）

(1)
図\(\,1\,\)をもっと簡単にすると、
椅子の後部と次の椅子の前の間隔は\(\,50\,\)ですが関係ありません。

椅子が\(\,1\,\)個増えると\(\,90\,\)増えるということです。

①
椅子の個数を\(\,x\,\)として、\(\,\mathrm{OP}\,\)の長さを\(\,y\,\)とします。　

関数では\(\,x,y\,\)が何を表しているかをしっかり理解しておくことが大切ですね。

椅子の個数が\(\,1\,\)個増えると\(\,90\,\)ずつ増えます。

　\(\,x=4\,\)　のとき椅子は\(\,3\,\)個増えるので

\(\,y=40+90\times 3=\underline{　310　（ア）}\,\)

　\(\,x=7\,\)　のとき椅子は\(\,6\,\)個増えるので

　\(\,y=40+90\times 6=\underline{　580　（イ）} \,\)

②
①の規則性からも分かるように、

\(\,\mathrm{OP}\,\)の長さは、\(\,1\,\)個目の\(\,40\,\)に、
　椅子の個数より\(\,1\,\)個少ない\(\,90\,\)を加える

ので、

　\(\begin{eqnarray}
y&=&40+90\times (x-1)\\
&=&90x-50
\end{eqnarray}\)

(答え)　\(\underline{　y=90x-50　}\)

③
\(\,\mathrm{OP}\,\)が\(\,1660\,\)となるときとは聞かずに、
\(\,y=1660\,\)のときの\(\,x\,\)を聞いてきています。

何も考えず②で求めた関数に代入すれば良いだけですね。

　\(\begin{eqnarray}
1660&=&90x-50\\
90x&=&1660+50\\
&=&1710\\
x&=&\underline{　19　}
\end{eqnarray}\)

(3)
条件は

　\(\,\mathrm{O}\,\)から椅子を\(\,90\,\)の間隔で\(\,23\,\)個並べて、
　\(\,200\,\)のすき間を空けて、
　\(\,\mathrm{Q}\,\)から椅子を\(\,a\,\)の間隔で\(\,16\,\)個並べると\(\,3490\,\)

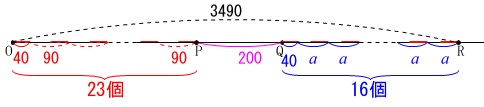
ということです。

①②のことから

　\(\begin{eqnarray}
\mathrm{\color{red}{OP}}&=&40+90\times (23-1)\\
&=&40+90\times 22\\
&=&40+1980\\
&=&\color{red}{2020}
\end{eqnarray}\)

　\(\begin{eqnarray}
\mathrm{\color{blue}{QR}}&=&40+a\times (16-1)\\
&=&\color{blue}{40+15a}
\end{eqnarray}\)

なので条件から方程式を立てて解くと

　\(\begin{eqnarray}
\color{red}{2020}+\color{magenta}{200}+\color{blue}{40+15a}&=&3490\\
2260+15a&=&3490\\
15a&=&3490-2260\\
&=&1230\\
a&=&\underline{　82　}
\end{eqnarray}\)

\(\,a\,\)の値を求めるだけなのでここまでです。

後半の方が問題数は少ないですが応用された問題があり長くなるのでここで区切ります。

⇒　2019年大阪府公立高校入試の数学B問題の解説【後半】　

\(\,\large{3}\,\)は平面図形の基本と応用問題

\(\,\large{4}\,\)は空間図形の基本と応用問題

となっています。

⇒　大阪府公立高校入試2018(平成30年度) 数学B問題の解説(問1)

問題構成は\(\,2018\,\)年と同じでした。