2019年大阪府公立高校入試の数学B問題の解説【後半】

2019年(平成31年度)に大阪府で行われた公立高校入試の数学B問題の問3問4の解説です。
3は平面図形の角度から相似の証明と線分の長さ、4は空間図形の基本用語の確認から立体の体積までの応用です。
計算量だけ見ても前半2問の倍くらいになりますので、ながめているだけでは答えは出ません。

問題は大阪府で公開してくれています。

⇒　2019年大阪B問題

\(\,\large{3}\,\),\(\,\large{4}\,\)ともに計算量は多いですが、高いレベルでの計算力が必要なわけではありません。
一つひとつ処理していけば最後までたどり着けます。
ただし、一気に答えが出る問題ばかりではないので手を動かさないと先には進めません。

3.平面図形

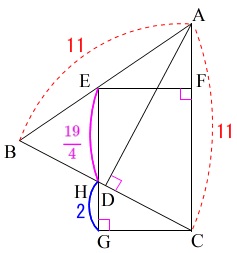
条件は

　\(\,\mathrm{AB=AC=11}\,\)
　\(\,\mathrm{EGCF}\,\)は長方形
　\(\,\mathrm{AC}\,\)　⊥　\(\,\mathrm{BC}\,\)

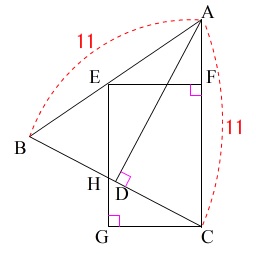
三角形の内角の和

(1)
　\(\,\mathrm{∠AEF}=a^{\circ}\,\)とするとき、
　\(\,\mathrm{∠EAF}\,\)を\(\,a\,\)を用いて表します。
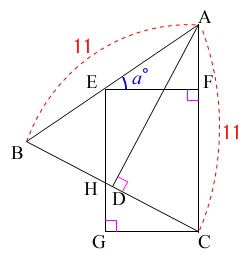\(\,\mathrm{△AEF}\,\)は直角三角形なので、

　\(\begin{eqnarray}
\mathrm{∠EAF}&=&90^{\circ}-\mathrm{∠AEF}\\
&=&90^{\circ}-a^{\circ}\\
&=&\underline{　90-a　}　(度)
\end{eqnarray}\)

三角形の内角の和を利用しただけです。

三角形の内角の和は\(\,180^{\circ}\,\)だから

　\(\mathrm{∠AFE}=90^{\circ}\)

のとき、残りの2つの角の和が\(\,90^{\circ}\,\)になるので

　\(\begin{eqnarray}
\mathrm{∠AEF+∠EAF}&=&90^{\circ}\\
\mathrm{∠EAF}&=&90^{\circ}-\mathrm{∠AEF}
\end{eqnarray}\)

となります。
直角三角形の場合、直角以外の\(\,2\,\)角の和が\(\,90^{\circ}\,\)になるというのは当たり前ですよね。

相似の証明

(2)
相似の証明です。

先ずは図の中で証明を終わらせておくことです。
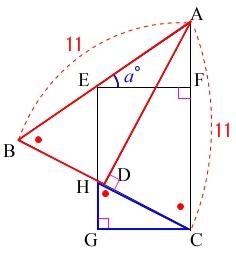\(\,\mathrm{△ABC}\,\)が二等辺三角形であることと、
\(\,\mathrm{EGCF}\,\)が長方形であることを利用すれば1つ角が等しいことが言えて、
後は仮定から直角を両方の三角形が持つことをいえば終わりです。

(証明)
　\(\,\mathrm{△ABD}\,\)　と　\(\,\mathrm{△CHG}\,\)　において

仮定から

　\(\,\mathrm{∠ADB=∠CGH=90^{\circ}}\,　･･･①\)

\(\,\mathrm{△ABC}\,\)は二等辺三角形なので

　\(\mathrm{∠ABD=\color{red}{∠ACD}}　･･･②\)

また\(\,\mathrm{EGCF}\,\)は長方形なので\(\,\mathrm{EG\,/\!/\,FC}\,\)だから、
錯角が等しいことから

　\(\mathrm{∠CHG=\color{red}{∠ACD}}　･･･③\)

②③から

　\(\,\mathrm{∠ABD=∠CHG　･･･④}\,\)

①④から

　\(\,2\,\)組の角がそれぞれ等しい

ので

　\(\,\mathrm{△ABD}\,\)　∽　\(\,\mathrm{△CHG}\,\)
(終わり)

相似を利用した線分の長さの求め方

(3)
長さの条件が加わります。

　\(\,\mathrm{HG=2}\,\)
　\(\,\mathrm{HC=5}\,\)
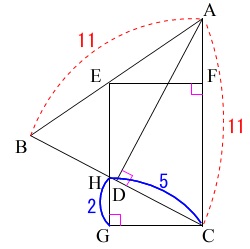①\(\,\mathrm{BD}\,\)の長さを求めます。
(2)の結果を利用しましょう。

　\(\,\mathrm{△ABD}\,\)　∽　\(\,\mathrm{△CHG}\,\)
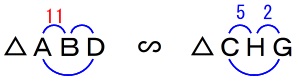より、
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:CH}&=&\mathrm{BD:HG}\\
11:5&=&\mathrm{BD}:2\\
5\times \mathrm{BD}&=&11\times 2\\
\mathrm{BD}&=&\underline{　\frac{22}{5}　(\mathrm{cm})}
\end{eqnarray}\)
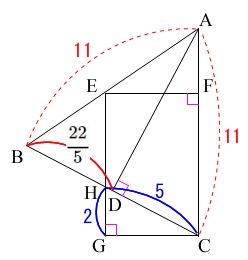すべての長さが出そうですが、
求めたいのは\(\,\mathrm{FC}\,\)の長さなので、
\(\,\mathrm{FC}\,\)か\(\,\mathrm{EG}\,\)が求まりそうになるところでやめておきましょう。

　\(\displaystyle \mathrm{BD}=\frac{22}{5}\)

なので

　\(\begin{eqnarray}\displaystyle
\mathrm{BC}&=&2\times \frac{22}{5}\\
&=&\color{red}{\frac{44}{5}}
\end{eqnarray}\)

このことから

　\(\begin{eqnarray}\displaystyle
\mathrm{BH}&=&\color{red}{\frac{44}{5}}-\color{blue}{5}\\
&=&\color{magenta}{\frac{19}{5}}
\end{eqnarray}\)

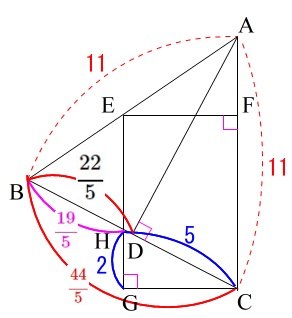何故弧の長さを出しに行っているかというと、方向性が見えているからではありません。
前の問題を無意味にしないために使っているだけです。

必ず意味があるとは限りませんが、その問題以前にある条件は使う、それが基本です。

ここで\(\,\mathrm{FC＝EG}\,\)なので\(\,\mathrm{EG}\,\)を求めれば良いのですが、

　\(\,\mathrm{EG=GH+HE}\,\)

で\(\,\mathrm{GH=\color{blue}{2}}\,\)は問題にある長さだから\(\,\mathrm{HE}\,\)が求められれば\(\,\mathrm{FC}\,\)が分かります。

\(\,\mathrm{EH\, /\!/ \,FC}\,\)なので

\(\,\mathrm{△BHE}\,\)　∽　\(\,\mathrm{△BCA}\,\)
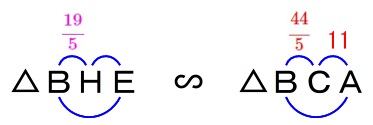なので

　\(\begin{eqnarray}
\mathrm{BH:BC}&=&\mathrm{HE:CA}\\
\frac{19}{5}:\frac{44}{5}&=&\mathrm{HE}:11\\
19:44&=&\mathrm{HE}:11\\
44\times \mathrm{HE}&=&19\times 11\\
\mathrm{HE}&=&\frac{19\times 11}{44}\\
&=&\color{magenta}{\frac{19}{4}}
\end{eqnarray}\)

よって

　\(\begin{eqnarray}
\mathrm{FC}&=&\mathrm{EG}\\
&=&\mathrm{GD+HE}\\
&=&\color{blue}{2}+\color{magenta}{\frac{19}{4}}\\
&=&\underline{　\frac{27}{4}　(\mathrm{cm})}
\end{eqnarray}\)

三平方の定理と考えて進めた場合は大きな数値をあつかう計算が待っています。
（一応やってみましたが、途中でやめました。笑）

問題の誘導に乗れば割ときれいな数値で相似の利用だけで終わりました。

4.空間図形

条件が多いように見えますが、まとめて見るとわかりやすい立体です。

条件

　\(\,\mathrm{ABCD-EFGH}\,\)は四角柱
　\(\,\mathrm{ABCD}\,\)は台形で
　　\(\,\mathrm{BC\,/\!/\,AD}\,\)
　　\(\,\mathrm{∠BCD=∠ADC=90^{\circ}}\,\)
　　\(\,\mathrm{BC=2\,,\,AD=DC=4}\,\)
　\(\,\mathrm{CGHD\,,\,ADHE}\,\)は\(\,1\,\)辺\(\,4\,\)の正方形
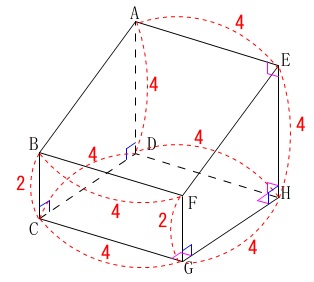つまり、立方体の上部を斜めに切り取った立体です。

(1)
\(\,\mathrm{AD}\,\)の中点を\(\,\mathrm{I}\,\)とするときの位置関係と長さと面積の問題です。

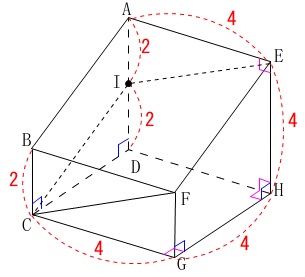
ねじれの位置とは？

①
ねじれの位置にある辺を探します。

辺\(\,\mathrm{AE}\,\)とねじれの位置にあるのは、
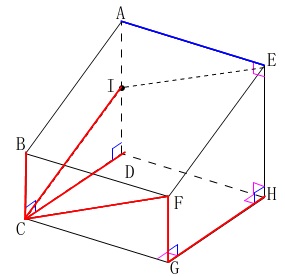同一平面上に無く、平行でも無い直線のことです。
直線なので延長しても交わりを持ってはダメですが、ここでは関係ありません。

　ア　辺\(\,\mathrm{DH}\,\)は平行
　イ　辺\(\,\mathrm{AB}\,\)は交わりを持つ
　ウ　辺\(\,\mathrm{CG}\,\)は平行

なので
(答え)　\(\underline{　エ　}\,\mathrm{辺\,BC}\,\)

四角形の対角線の長さとひし形の面積

②
四角形\(\,\mathrm{EFGH}\,\)の対角線\(\,\mathrm{EG}\,\)の長さを求めます。
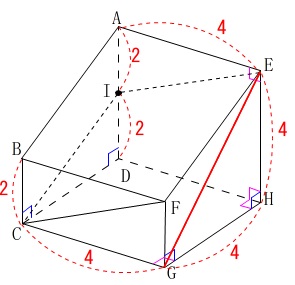\(\,\mathrm{△EGH}\,\)は直角二等辺三角形（三角定規）なので

　\(\mathrm{EH:EG}=1:\sqrt{2}\)

よって

　\(\begin{eqnarray}
\mathrm{EF}&=&\sqrt{2}\times\mathrm{EH}\\
&=&\sqrt{2}\times \color{red}{4}\\
&=&\underline{　4\sqrt{2}　}　(\mathrm{cm})
\end{eqnarray}\)

もちろん、三平方の定理でも良いですよ。

③
四角形\(\,\mathrm{EICF}\,\)の面積を求めます。
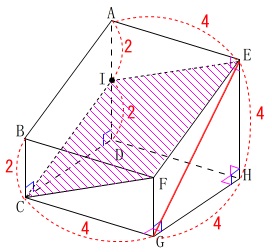問題にも書いてある通り、ひし形です。

抜き出して見てみましょう。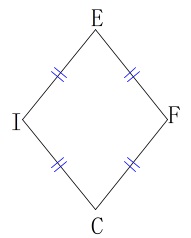ひし形の\(\,1\,\)辺の長さ\(\,\mathrm{IC}\,\)は、
直角三角形\(\,\mathrm{AIE}\,\)の斜辺なので

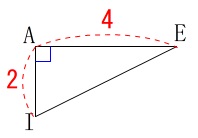
　\(\begin{eqnarray}
\mathrm{IE^2}&=&\mathrm{AI^2+AE^2}\\
&=&2^2+4^2\\
&=&20\\
\mathrm{IE}&=&\color{magenta}{2\sqrt{5}}　(\mathrm{IE}＞0)
\end{eqnarray}\)

また、対角線\(\,\mathrm{IF}\,\)の長さは、正方形\(\,\mathrm{DCGH}\,\)の対角線なので、

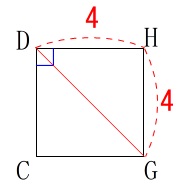
　\(\,\mathrm{IF}=\color{red}{4\sqrt{2}}\,\)

ひし形の対角線の交点を\(\,\mathrm{K}\,\)とすると

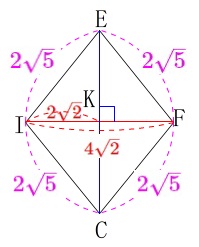
　\(\,\mathrm{IK}=\color{red}{2\sqrt{2}}\,\)

なので三平方の定理から

　\(\begin{eqnarray}
\mathrm{EK^2+IK^2}&=&\mathrm{IE^2}\\
\mathrm{EK}^2+(\color{red}{2\sqrt{2}})^2&=&(\color{magenta}{2\sqrt{5}})^2\\
\mathrm{EK}^2+8&=&20\\
&=&20-8\\
&=&12\\
\mathrm{EK}&=&\color{blue}{2\sqrt{3}}　(\,\mathrm{EK}\,＞\,0\,)
\end{eqnarray}\)

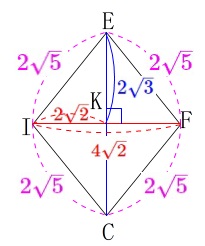
よってひし形\(\,\mathrm{EICF}\,\)の面積は

　\(\hspace{10pt}\color{red}{4\sqrt{2}}\times \color{blue}{2\sqrt{3}}\\
=\underline{　8\sqrt{6}　}　(\,\mathrm{cm^2}\,)\)

ひし形の面積\(\,\mathrm{S}\,\)は対角線の長さを\(\,\color{blue}{a},\color{red}{b}\,\)とすると、

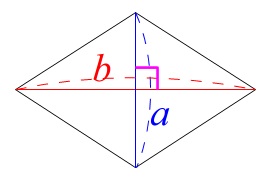
　\(\displaystyle S=\frac{1}{2}\times \color{blue}{a}\times \color{red}{b}\)

ということは算数でやってますよね。

(2)
条件が加わります。

　\(\,\mathrm{H}\,\)から\(\,\mathrm{EF}\,\)に垂線を引いて交点を\(\,\mathrm{J}\,\)とする

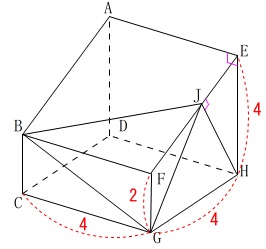
立体の体積は後なので色はつけていません。

垂線の長さの求め方

①
線分\(\,\mathrm{EJ}\,\)の長さを求めます。

垂線\(\,\mathrm{HJ}\,\)を引きましたが、\(\,\mathrm{EJ}\,\)も見る角度を変えると垂線です。

垂線の長さの求め方はいくつもあります。

三平方の定理はすぐに思いつくでしょうが、斜辺と他の\(\,1\,\)辺の長さが分かっていないと使えません。

底辺の分かっている三角形の面積を利用して求めることも多いです。
その場合は底辺の長さと面積が必要になります。

他にも、相似を利用することも多いです。

どれを使うかは自分で決めて良いです。
数学の答えの出し方は1つではありませんよ。

いずれにしても\(\,\mathrm{EJ}\,\)を含む面を抜き出しましょう。
四角形\(\,\mathrm{EFGH}\,\)です。

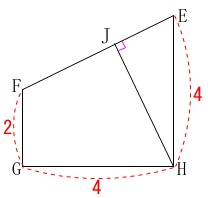さて、何を使いましょう？

いっておきますが試験会場では何が一番近道かなんて考えているヒマはないですよ。
思いついた方法で突っ走った方がはやい場合が多いです。

問題集の解法はいろいろな解法のうち、一番きれいと思える解法が載せてあるだけです。笑

三平方の定理にしては辺の長さが不足しているのですぐには使えません。

補助線を引きますが、有効な補助線は垂線か、平行線がほとんどです。

平行線を引くと相似な三角形が出てくるので相似を利用してみましょう。

\(\,\mathrm{F}\,\)から\(\,\mathrm{EH}\,\)に垂線を引いて\(\,\mathrm{EH}\,\)との交点を\(\,\mathrm{M}\,\)としましょう。

　\(\,\mathrm{△FEM}\,\)　∽　\(\,\mathrm{△HEJ}\,\)

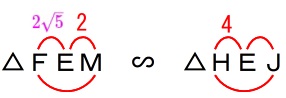
なので

　\(\begin{eqnarray}\displaystyle
\mathrm{FE:HE}&=&\mathrm{EM:EJ}\\
2\sqrt{5}:4&=&2:\mathrm{EJ}\\
2\sqrt{5}\times \mathrm{EJ}&=&4\times 2\\
\mathrm{EJ}&=&\frac{4\times 2}{2\sqrt{5}}\\
&=&\underline{　\frac{4\sqrt{5}}{5}　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)

\(\,\mathrm{△EFH}\,\)の面積を利用して、

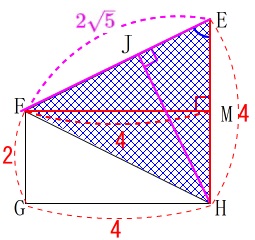
　\(\displaystyle \mathrm{△EFH}=\frac{1}{2}\times \mathrm{\color{red}{FM}}\times \mathrm{\color{red}{EH}}\)
であり、
　\(\displaystyle \mathrm{△EFH}=\frac{1}{2}\times \mathrm{\color{magenta}{EF}}\times \mathrm{\color{magenta}{HJ}}\)
であって、面積は同じなので、

　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times \color{red}{4}\times \color{red}{4}&=&\frac{1}{2}\times \color{magenta}{2\sqrt{5}}\times \mathrm{\color{magenta}{HJ}}
\end{eqnarray}\)

から\(\,\mathrm{\color{magenta}{HJ}}\,\)を求めて\(\,\mathrm{△EHJ}\,\)に三平方の定理を使っても求まります。

それほど時間はかからないのでやってみて下さい。
三角形は転がしても面積は変わらないというのはよく使うので覚えおくと良いです。

線分比を利用した体積の求め方

②
立体\(\,\mathrm{BFGH}\,\)の体積です。
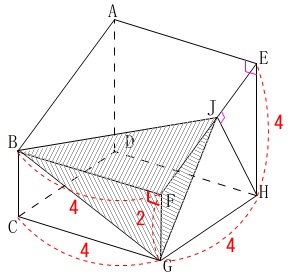立体は三角錐で高さとなるのは垂線になっている\(\,\mathrm{BF}\,\)と分かりますが、
底面積が出ていません。

高さを\(\,\mathrm{BF}\,\)と見ると底面は\(\,\mathrm{△FGJ}\,\)です。
底面となる\(\,\mathrm{△FGJ}\,\)の面積を求めにいきましょう。

①から

　\(\displaystyle \mathrm{EJ}=\color{blue}{\frac{4\sqrt{5}}{5}}\)

なので

　\(\begin{eqnarray}\displaystyle
\mathrm{FJ}&=&\mathrm{FE-EJ}\\
&=&\color{magenta}{2\sqrt{5}}-\color{blue}{\frac{4\sqrt{5}}{5}}\\
&=&\frac{10\sqrt{5}-4\sqrt{5}}{5}\\
&=&\color{red}{\frac{6\sqrt{5}}{5}}
\end{eqnarray}\)

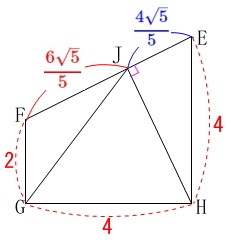\(\,\mathrm{J}\,\)から直線\(\,\mathrm{GF}\,\)に垂線を引いて高さを求めても良いですが、
線分比を利用して面積を出す方が先に思いついたので\(\,\mathrm{△EFG}\,\)の値を利用します。
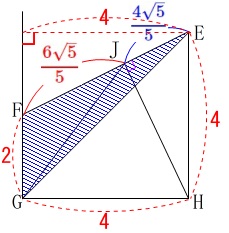\(\,\mathrm{△EFG}\,\)の高さは\(\,\mathrm{GH}\,\)と同じなので、

　\(\begin{eqnarray}
\mathrm{△EFG}&=&\frac{1}{2}\times 2\times 4\\
&=&\color{blue}{4}
\end{eqnarray}\)

ここで

　\(\begin{eqnarray}
\mathrm{EJ:JF}&=&\color{blue}{\frac{4\sqrt{5}}{5}}:\color{red}{\frac{6\sqrt{5}}{5}}\\
&=&\color{blue}{2}:\color{red}{3}
\end{eqnarray}\)
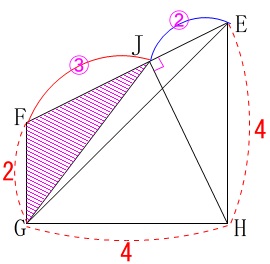なので、

　\(\begin{eqnarray}
\mathrm{△FGJ}&=&\frac{3}{5}\times \mathrm{△EFG}\\
&=&\frac{3}{5}\times \color{blue}{4}\\
&=&\color{magenta}{\frac{12}{5}}
\end{eqnarray}\)

⇒　神奈川県公立高校入試2018の数学問4関数と図形融合問題の解説

底辺の比と面積比については基本的なことで全国の入試であつかわれていますが、
神奈川入試で応用問題が出ているので見ておくと良いでしょう。

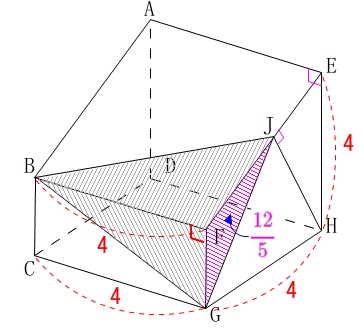
よって求める体積\(\,\mathrm{V}\,\)は、

　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \mathrm{△FGJ}\times \mathrm{BF}\\
&=&\frac{1}{3}\times \frac{12}{5}\times 4\\
&=&\underline{　\frac{16}{5}　} 　(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

ここでは区切りとして途中でいちいち計算していますけど、本番では最後にまとめて計算すれば良いですよ。

これで\(\,2019\,\)年の大阪府公立高校入試\(\,\mathrm{B}\,\)問題はすべて終わりです。

すべてきれいな数値で終わりましたが、
基本的なことは偏り無く出題されています。

⇒　2019年(平成31年度)大阪府公立高校入試の数学B問題の解説

基本を身につけて、それらを応用できるように手を動かすことがポイントになります。

⇒　大阪府公立高校入試2018(平成30年度) 数学B問題の解説(問1)

\(\,2018\,\)年も傾向は同じです。