座標とは位置を表すために使われますが、ここでは数学で使われる座標の使い方を説明しておきます。
さらに中学1年であつかう比例と反比例の関数のグラフの書き方と座標の求め方も解説しておきます。
座標の読み取りと書き方を覚えておかないと入試では関数の問題を捨てることになります。
座標を求める簡単な練習をいくつかしておきましょう。
座標とは
座標とはある点の位置を固定するために基準を決めて表された点のことです。
例えば地球上の地点を示すのに、日本の標準となる明石市は
\(東経 135 度 北緯 34.4 度\)
としますが、これはイギリスのグリニッジ子午線を経度0、赤道を緯度0として、
地球を東西方向一周を360度に分割したとき、
イギリスより東側を東経、西側を西経と180度に分け、
緯度については赤道を0度として北極を北緯90度、
南極を南緯90度としたときの位置関係を示しています。
この基準によって一つの地点には一つの座標が与えられることになります。
逆に一つの座標がわかればその地点がどこに位置するかがわかります。
この座標を数学では原点\(\,(\,0\,,\,0\,)\)を基準として、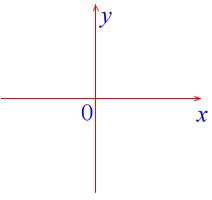
\(x\,軸を右に大きくなるように、\\
y\,軸を上に大きくなるように\)
定めます。
この軸方向は自分で定義しない限り変えることはありません。
中学生はすべて軸同士が垂直になるように統一しておきましょう。
\(\color{red}{x\,軸は右に大きく、\\
y\,軸は上に大きく、\\
垂直に交わる。}\)
\(x\) 軸だけで表す数直線も右に大きく取ることも同じように統一しておきましょう。
空間座標はまだあつかいませんが、これも基本的には統一します。
\(\,x-y-z\,\)の順に反時計回りに設置しますが、高校で確認してください。
点を座標で表し、座標を読み取る
軸を \(x,y\) とする座標を \(x-y\) 座標といいます。
座標は \(\color{red}{(\,x\,,\,y\,)}\) と表します。
左に \(x\) 座標、右に \(y\) 座標を書きます。
いくつか点を具体的に座標で表してみるとわかりやすいです。
練習してみましょう。
例えば、\(x=2\) がわかったとすれば、
\(xy\) 座標の \(x=2\) のどこかです。
これではどこにあるかまでは定まりません。
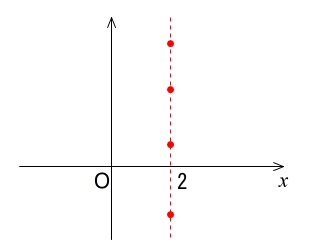
ここで \(y\) 座標が \(3\) だとわかれば、
\(x=2\,であり、y=3\) の位置にあるので1点に定まります。
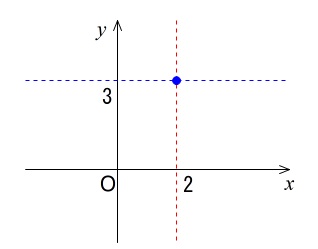
この点を座標 \((\,x\,,\,y\,)\,=\,(\,2\,,\,3\,)\) と表します。
座標を読み取る場合は逆です。
座標の \(x\) 座標を読み取り、\(y\) 座標を読み取り、まとめて座標で書き出すだけです。
座標を表している点から縦に移動して軸と交わったところが \(x\) 座標です。
座標を表している点から横に移動して軸と交わったところが \(y\) 座標です。
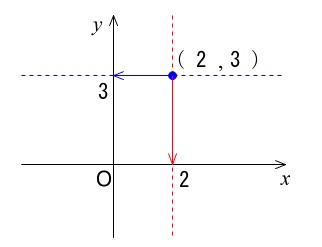
注意してほしいのは、
座標には \(x\) 座標と、 \(y\) 座標がありますが、
「座標」という場合は両方を表して座標といいます。
「座標を求めよ。」と問題にある場合は両方書くように注意してください。
\(x\) 座標だけでは「座標」ではありません。
ところで原点を表す記号は「 \(\mathrm{O}\) 」ですがこれは \(0(ゼロ)\)ではありません。
アルファベットの \(\mathrm{O}\)(オー)です。
原点 \(\mathrm{O}\,(\,0\,,\,0\,)\)
( \(x\) 座標と \(y\) 座標は \(0(ゼロ)\) です。)
座標とグラフ
グラフは座標上に書くことになりますが、
すべてのグラフは座標の集合体です。
だから一気に書くのではなく、いくつか点を取ってつなげば必ず書けます。
中学であつかう関数は四つで、それぞれ最低限の点さえわかれば書くことはできます。
例えば、比例だと原点以外の1点、二年で習う1次関数だと2点、など最低の座標数でグラフは書けます。
しかし、グラフは点の集まりだということを忘れなければ、
複雑なグラフもすべて書くことができるのです。
比例のグラフ
比例のグラフは簡単です。
比例のグラフは原点を通る直線なので、原点以外の1点がわかればすぐに求まります。
しかし、いくつか関数を満たす座標を打ってつなげば書けます。
例えば \(y=2x\) のグラフは、
| \(x\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(-2\) | \(0\) | \(2\) | \(4\) | \(6\) |
この点たちをつなぐことをグラフの書き方の基本にしておいてください。
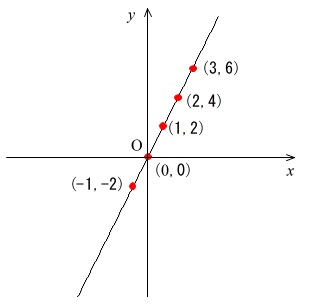
いずれ直線は2点で書けるようになりますが、数点を座標に書き込んで結んで下さい。
時間が多少かかりますが書けないグラフはありません。
※
直線を定規で書くときはできるだけ遠い2点を結ぶとずれが少なくなります。
反比例のグラフ
反比例のグラフは2点を結ぶとかでは定まりません。
いくつか点を決めないと書きにくいです。
おおよその形(概計(がいけい)といいます)はすぐに書けますが、
点を一致させるにはいくつか点が必要です。
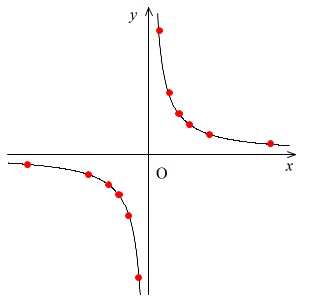
例えば、\(\displaystyle y=\frac{12}{x}\) は反比例です。
反比例のグラフの形は双曲線になります。
しかし、いくつか点を取れば必ず書けます。
\(\,x\,,\,y\,\) ともに整数になる点を取り出してみます。
マイナス側もあるので忘れないようにしてください。
| \(x\) | 1 | 2 | 3 | 4 | 6 | 12 |
| \(y\) | 12 | 6 | 4 | 3 | 2 | 1 |
| \(x\) | -12 | -6 | -4 | -3 | -2 | -1 |
| \(y\) | -1 | -2 | -3 | -4 | -6 | -12 |
これをなめらかにつなげばグラフのできあがりです。
座標を求める問題の解き方
座標を移動させた点の座標を求めてみます。
座標が読み取れているかの確認になりますので手を抜かない方が良いですよ。
問題2 次の点の座標を求めなさい。
(1) 点 \((\,5\,,\,10\,)\) と \(x\) 軸, \(y\) 軸,原点についてそれぞれ対称な点
(2) 点 \((\,4\,,\,-7\,)\) を左へ \(9\) ,上に \(10\) だけ移動した点
(3) 2点 \((\,-6\,,\,7\,)\) ,\((\,4\,,\,3\,)\) の真ん中の点
これから数学をやる上で重要なポイントをお伝えしておきます。
座標も(グラフも)、図形も、頭の中だけで考えないようにしましょう。
どこでも言っているので何度も目にすることだとは思いますが、
グラフや図形を書かないというのは、「わからない」ではなくて、解く気がないのと同じです。
頭の中で考えられるようになったときには、ここにはいないはずです。笑
それまでは、できるだけ「見てわかる」ように書き出してください。
それでも全国トップクラスには入れます。
(1) 点 \((\,5\,,\,10\,)\) と \(x\) 軸, \(y\) 軸,原点についてそれぞれ対称な点
座標を書けば簡単です。
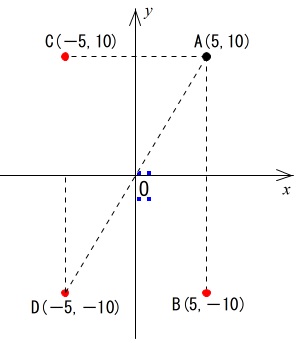
点 \(\,\mathrm{A}\,\) \((\,5\,,\,1\,0)\) の \(x\) 軸に対称な点は \(\,\mathrm{B}\,\) ですが、
縦に動いただけなので、\(x\) 座標は同じで, \(y\) 座標はマイナスになります。
答えは \(\underline{(\,5\,,\,-10\,)}\) 。
これが \(x\) 軸に対称な点の座標です。
同じように \(y\) 軸対称な点は、横に動くだけなので \(\,\mathrm{A}\,\) と \(y\) 座標が同じで \(\underline{(\,-5\,,\,10\,)}\)。
原点対称な点は、\(x\) も \(y\) も反対になるので、 \(\underline{(\,-5\,,\,-10\,)}\)。
対称な点を求められない人は高校生にもいますが座標上で見てください。
数学で単に「対称」と言えば線対称を意味していることも高校生は忘れずに!
(2) 点 \((\,4\,,\,-7\,)\) を左へ \(9\) ,上に \(10\) だけ移動した点
これも座標を書いて考えれば簡単です。
ただ、座標、とか、点、といわれれば、
\(\,(\,a\,,\ b)\,\)の形で答えましょう。
\(\,(\,a\,,\ b)\,\)の中の左側 \(a\) が \(x\) 座標で、右側 \(b\) が \(y\) 座標と決まっています。
覚えておきましょう。
\(( \color{red}{\,x\,座標} , \color{blue}{y\, 座標} )\)
先ず、「左へ9」移動だから \(x\) 座標だけが-側に変化します。
その後「上に10」移動だから \(y\) 座標だけが+側に変化します。
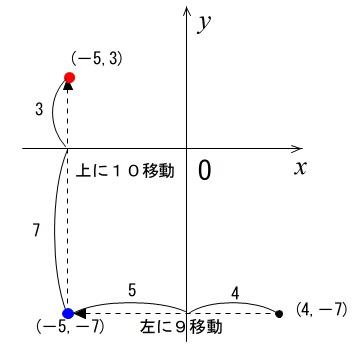
座標から見て、答えは \(\underline{(\,-5\,,\,3)}\,\)。
ね?座標上で動かせば簡単でしょう?
慣れても数字で考えちゃダメですよ。
(3) 2点 \((\,-6\,,\,7\,)\) ,\((\,4\,,\,3\,)\) の真ん中の点
2つの点の真ん中の点を「中点(ちゅうてん)」といいます。
中点の出し方は『覚え太郎』のカードにもあるので計算で一瞬にしてでますが、
やはり座標上で確認しながら出すことを今は心掛けて下さい。
座標に慣れるためと、図を書いて考えるくせを付けてくためです。
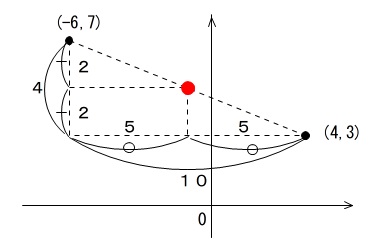
図でわかるように、
\(x\) 座標の差が \(\,10\,\) で半分は \(\,5\,\)
\(y\) 座標の差が \(\,4\,\) で半分は \(\,2\,\)
なのでそれぞれ、半分ずつ動かせば良いだけです。
座標上だと難しくないでしょう?
中点は \(\underline{(\,-1\,,\,5\,)}\)
計算で出すのも簡単ですよ。
\( x\,座標の二つと\,y\,座標の二つをそれぞれ足して\,2\,で割る\)
だけです。
\((\,\color{red}{-6}\,,\,\color{blue}{7}\,)\) と \((\,\color{red}{4}\,,\,\color{blue}{3}\,)\) で、
\(x\) 座標どうしを足すと \(-6+4=-2\)(これを2で割る)
\(y\) 座標どうしを足すと、\(7+3=10\)(これを2で割る)
それぞれを2で割って、中点は \(\underline{(\,-1\,,\,5\,)}\)。
計算でも出せる方が良いです。
圧倒的に時間短縮になりますから。
しかし、座標に慣れるために、それと高校になっても問題の意味がとれるように簡単にで良いから座標で示した方が良いですよ。
座標はこれからずっとついてきます。
ここが始まりになりますが、最後まで約束事は変わりません。
次は比例と反比例の関数を求めてみましょう。
⇒ 比例と反比例の関数の比例定数を決める問題の解き方と座標の求め方
中学の数学、というか高校入試の関数問題は関数決定できるかが大きなポイントになります。
