比例と反比例の関数のグラフの形や座標などのまとめ

中学1年の関数、比例と反比例のグラフの形と座標の名前などのまとめです。
比例は2年以降であつかう関数1次関数の一部だからもう一度やりますが、反比例につながる関数は2，3年ではありません。
難しくはないのですが、忘れていることもあるので復習項目にあげておかなければなりません。

２つの関数　比例と反比例

関数は初めてになりますがむずかしい単元ではありません。
ただ、文章題ではものすごく重要な単元です。
座標という新たな用語のも出てきますので軸や座標の名前を覚えておく必要があります。

そして、グラフというみんなが誤解しているものを始めて習う単元でもあります。
文章題では、ほとんどが比例関係にあるものなので心配しなくても大丈夫です。
全部じゃないですよ。
歯車の問題なんかは反比例ですよね。

⇒　関数が比例しているか反比例しているか？関係式の作り方と見分け方

比例の式の立て方に重点をおいて勉強していれば、理科でも多いに活躍してくれます。
数学でも多くの問題が乗り切れるようになります。

ただ、比例・反比例は関数として、「座標」という新しい言葉が出てくるのでグラフがどうだこうだと難しく考えすぎなんです。
まずは、「関数」とはどういうものかしっかり理解しておくことを優先しておいて下さい。
問題を解く解きに何をすれば良いかが少しは見えてくるでしょう。

関数とは、

　\(\color{red}{\large{\,x\,を決めれば\,y\,が１つ決まる関係}}\)

のことです。

比例のグラフと座標軸

比例は2年生になれば習いますが\(\,1\,\)次関数の特別な形で、原点を通る直線です。

⇒　1次関数とは？傾きや切片、変域などの用語と関数の増加減少

比例の関数は

　\(\color{red}{\large{y=ax}}　\)

となります。

グラフについては座標を使いますので、
\(\,x\,\)と\(\,y\,\)の関数とすると、

　\(\color{red}{\,x\,が増えれば}\\
\color{red}{\,y\,も一定の割合で増えるか}、\color{blue}{減るか}\)

です。

比例のグラフは、原点を通る直線ですが、右上がりと、右下がり両方あります。

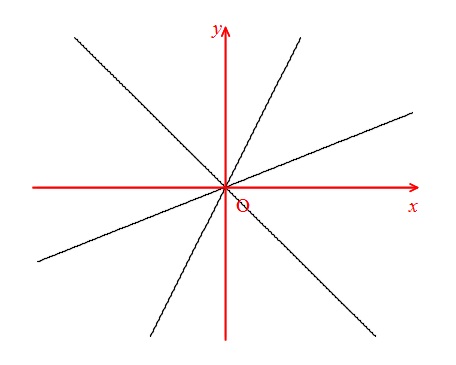
赤い線で示した矢印線を軸といいます。

横の右方向に大きくなるように\(\,x\,\)軸、
縦の上方向に大きくなるよう\(\,y\,\)軸を取るのが習慣となっていますので、
自分で勝手に変えることはしない方が良いです。
２つの軸が交わる点は「原点」です。

⇒　座標とは？比例と反比例の関数のグラフと座標の求め方

反比例のグラフ(双曲線)

反比例の関数は

　\(\color{red}{\displaystyle y=\frac{a}{x}}　\)

です。

反比例は、\(\,xy\,\)座標で考えると、
\(\,x\,\)が増えると、\(\,y\,\)は増えたり、減ったりして、一定ではありません。

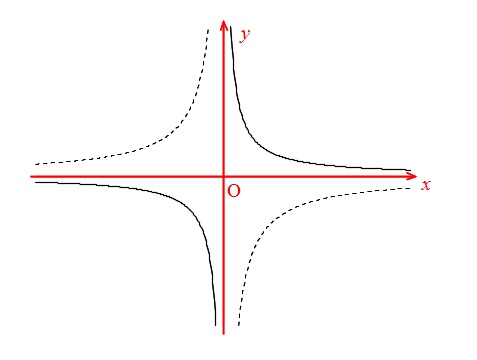
これはグラフを見ればすぐにわかることです。

この関係がよく解っていないとこの分野だけでなく文章題でつまずくのです。

といっても、文章題はほとんどが比例の関係ですので、反比例だけは別物と考えておいた方が取り組みやすいかもしれません。

文章題でも反比例はでますが、グラフで使うのは右上の部分と思っていて良いくらいですね。

グラフの特徴は、

反比例は、双曲線と呼ばれる、\(\,x\,\)軸と\(\,y\,\)軸にどんどん近づく曲線です。

高校の数学では、双曲線は違う定義をしますが、
中学では直角双曲線と呼ばれる、\(\,x\,\)軸と\(\,y\,\)軸を漸近線（ぜんきんせん）とするものだけを学びます。
ややこしいので無視して下さい。（笑）

少しレベルを上げてみると、反比例のグラフ上のある点を取って、

　軸と平行に線を引いてできる長方形をつくると面積が一定になる

⇒　比例と反比例のグラフから三角形,四角形の面積を求める問題の解き方

ということもあるのですが、先ずはグラフの形を覚えておきましょう。

比例と反比例に共通する比例定数

　\(　比例　y=\color{red}{a}x　\)
　\(　反比例　\displaystyle y=\frac{\color{red}{a}}{x}\)
において、
　\(\,\color{red}{a}\,\)を共通で「\(\,\color{red}{比例定数}\,\)」と呼びます。

１次関数だけが違うので再度確認することになりますが、
比例でも、反比例でも「比例定数」と呼ぶことは覚えておきましょう。

⇒　比例と反比例の関数の比例定数を決める問題の解き方と座標の求め方

比例も反比例も関数なので、グラフを書いて考えるようにすると良いですよ。

というか、
関数を考えるときグラフ無しで考えるようになると、高校に進んだとき必ず数学は苦手な科目になっています。

中学の内から関数として考えられる問題は、すべてグラフをイメージしながら、
できれば簡単なグラフを書きながら問題に当たるようにしておきましょう。

比例も反比例もまた例題をあげて説明することにします。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

２年生以上の人は１次関数との違いは見なおしておいてください。

関数の見分け方は \(x\,,\,y\) の関係式を出せばすぐにわかります。

⇒　関数が比例しているか反比例しているか？関係式の作り方と見分け方

比例と反比例の見分け方です。