比例と反比例のグラフから三角形,四角形の面積を求める問題の解き方

比例や反比例の関数問題で、グラフ上の点と関係する三角形や四角形の面積を求める問題の解き方です。
座標を利用することになりますが、求める面積の形が三角形でも四角形でも求め方は簡単です。
比例、反比例だけでなく関数すべて、ひとつの方針で解けるのでややこしいことは考えなくて良いです。

いくつか問題を解きながら説明します。
その中で共通してすることが見えてきますので確認してください。

関数、座標が関係する問題すべて入試まで同じ方法で通用します。

比例や反比例のグラフと面積の求め方の共通点

比例のグラフが直線になります。
反比例のグラフは双曲線という曲線になります。

⇒　比例と反比例の関数のグラフの形や座標などのまとめ

しかし、（高校入試までに限れば、）
　「\(\color{red}{面積を求めなさい。}\)」
という問題で、曲線部分を含む面積を求めるのは、円が関係する問題以外ありません。

だから反比例のグラフ、双曲線を意識する必要は全くありません。

比例でも、反比例でも、二年で習う一次関数でも、三年で習う２次関数でも、

　『三角形か四角形の面積を求める』

ことだけを考えれば良いのです。

四角形も三角形２つに分けられるので、

　『すべて三角形の面積を求める』

といっても良いでしょう。

そもそも、双曲線の囲む面積は普通の高校生でも求められません。
理系に進んだ人だけが求めることができます。

では関数の面積問題では何をすれば良いのか？

　\(\Large{\color{red}{グラフや座標を書き出す！}}\)

それだけです。

比例のグラフと面積を求める問題の解き方

普通は簡単な問題だと図が与えられ「図のように」と書かれますが、
ここでは図を自分で書くことを意識できるようにわざと日本語で書きます。

なので、ここでなれておくと普通のテスト問題や入試問題も簡単に思えてきます。
めんどくさがらずに図を書くクセをつけておきましょう。
中１の比例、反比例の段階でこれができていると後の関数で苦労することはありません。

問題４-(1)
関数 \(y=2x\) 上の点 \((\,2\,,\,4\,)\) を A とする。
点 A から \(y\) 軸に平行な線を引き、\(x\) 軸との交点を B としたとき、
\(\triangle \mathrm{OAB}\) の面積を求めなさい。

まずは後に続く問題を解くための図を書く基本練習です。

　\(y=2x\) は比例で原点を通る直線です。
　点 A \((\,2\,,\,4\,)\) は直線上にあります。
　点 A から \(y\) 軸に平行に線を引きます。

これを図示します。

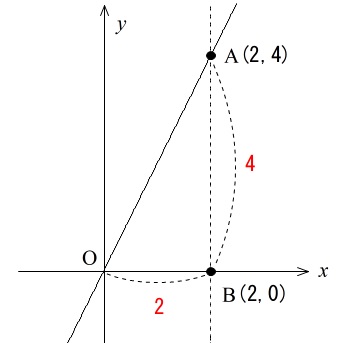
　\(y\) 軸に平行な線は縦の線になるので間違えないようにしましょう。
　\(x\) 軸に平行な線は横の線になります。

重要なポイントは、
　「交点といえる点はすべて座標を書き出しておく。」
ということです。

ムダな点も出てくるかもしれません。
でも、すべての交点が出せれば入試問題のすべてが解けます。

時間がかかりそうな場合があるし、試験時間に限りがあるので実際の試験ではほとんどの人が問題に聞かれた（問われた）点だけを求めようとします。
それでも解ける問題は多いのですが、入試問題ではここが関数での大きな差となります。

このことは２次関数をやって入試レベルの問題解説のときに詳しくします。

今は簡単なのであまり気にしなくても図を書いてみると交点はでています。

\(\triangle \mathrm{OAB}\) の面積は、
\(\,\mathrm{OB}\,\) を底辺、\(\,\mathrm{AB}\,\) を高さとする三角形の面積なので、

　\(\hspace{10pt}\displaystyle \frac{1}{2}\times \mathrm{OB} \times \mathrm{AB}\\
\displaystyle =\frac{1}{2}\times 2 \times 4\\
=\,4\)

次も比例ですが少しややこしくします。笑

問題４-(2)　次の問いに答えよ。
点 \(\,\mathrm{P}\,\) は比例 \(\displaystyle y=\frac{3}{4}x\) のグラフ上の点である。
点 \(\,\mathrm{P}\,\) から \(y\) 軸， \(x\) 軸にそれぞれ平行な直線をひき，
比例 \(\displaystyle y=-\frac{3}{2}x\) のグラフとの交点を \(\,\mathrm{A}\,\) ，\(\,\mathrm{B}\,\) とする。
点 \(\,\mathrm{P}\,\) の \(x\) 座標が \(\,8\,\) のとき，三角形PABの面積を求めよ。

普通はグラフがありますが自分で書きます。

　比例 \(\displaystyle y=\frac{3}{4}x\) のグラフは原点を通る直線です。
　比例 \(\displaystyle y=-\frac{3}{2}x\) のグラフも原点を通る直線です。
　点\(\,\mathrm{P}\,\)の座標は \(x\) 座標が \(8\) なので \(y\) 座標は
　\(\displaystyle y=\frac{3}{4}\times (8)=6\)　
よって点\(\,\mathrm{P}\,\)の座標は \((\,8\,,\,6\,)\) です。

ここまでを図示すると、点\(\,\mathrm{P}\,\) \((\,8\,,\,6\,)\) と、

　\(\,\mathrm{A }\,\)は \(\color{red}{x}\) 座標が同じで、\(\displaystyle y=-\frac{3}{2}x\) で \(\color{red}{x=8}\) のとき

　\(\,\mathrm{B}\,\) は \(\color{blue}{y}\) 座標が同じで、\(\displaystyle y=-\frac{3}{2}x\) で \(\color{blue}{y=6}\) のとき

なので点 \(\,\mathrm{A}\,\) , \(\,\mathrm{B}\,\) も加えて、

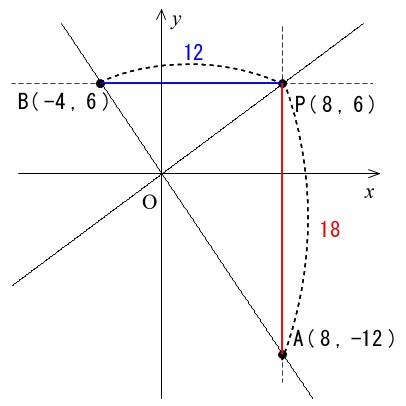
ついでに書き込みしておきましたが、

　\(\mathrm{PA}\) は \(\color{red}{y\,座標の差}\) なので、
　\(\mathrm{PA}=6-(-12)=18\)

　\(\mathrm{PB}\) は \(\color{blue}{x\,座標の差}\) なので、
　\(\mathrm{PB}=8-(-4)=12\)

よって　\(\triangle \mathrm{PAB}\)　の面積は

　\(\displaystyle \frac{1}{2}\times \mathrm{PA} \times \mathrm{PB}\\
\displaystyle =\frac{1}{2}\times 18 \times 12=\underline{108}\)

細かく説明を書いたので長くなりましたが、グラフ上で書き込むのにあまり時間はかかりませんよ。

交点を求める計算はしなくてはなりませんけど、単なる代入です。

ところでこの問題で \(\triangle \mathrm{OAP}\) の面積を求めるときは、

　底辺 \(\mathrm{=PA}\)
　高さ \(=\mathrm{P} の\,x\,座標\)　(\(\mathrm{A} の\,x\,座標も同じ)\)

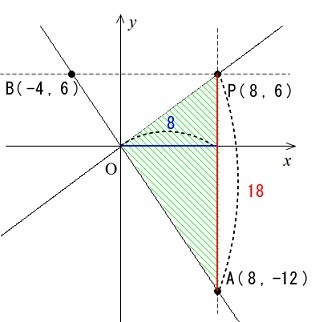
とする三角形の面積を求めれば良いということもみておいてください。
\(\triangle \mathrm{OBP}\) の面積も同様です。

反比例のグラフと面積の求め方

反比例のグラフと面積が関係する問題の解き方も比例のときと同じです。

グラフ、座標上に各点を書き込む、それだけで求めるものは三角形の面積か、四角形の面積です。

反比例の場合、１つ特別な性質を持っています。
よく考えれば当たり前のことなのですが、知らないとなかなか気がつかない性質ですので加えてお伝えしておきます。

問題４－(3)次の問いに答えなさい。
反比例 \(\displaystyle y=\frac{6}{x}\) 上の点P \((\,2\,,\,3\,)\) がある。
点Pから \(y\) 軸と \(x\) 軸に平行な線を引いて、軸との交点をそれぞれ \(\,\mathrm{A}\,\)、\(\,\mathrm{B}\,\) とする。
このとき \(\triangle \mathrm{PAB}\) の面積を求めなさい。
また長方形 \(\mathrm{OAPB}\) の面積を求めなさい。

座標上の双曲線と各点を図に示します。

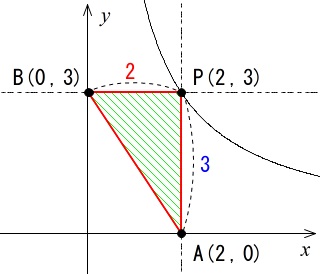
これは実際の試験会場では自分でやることになるので、普段から自分でやらないと意味はありませんよ。

問題集の解答は途中の過程が省かれていますので、
解答にある図をみて自分でやった気にならないことです。

座標が書き込めたら後は簡単ですね。

　\(\begin{eqnarray}
\displaystyle \triangle \mathrm{PAB}&=&\frac{1}{2}\times \mathrm{PA}\times \mathrm{PB}\\
\displaystyle &=&\frac{1}{2}\times 3 \times 2\\
&=&3
\end{eqnarray}\)

四角形 \(\mathrm{OAPB}\) の面積は長方形なので、
　\(\mathrm{PA}\times \mathrm{PB}=3\times 2=6\)

または \(\triangle \mathrm{PAB}\) の面積の2倍（2つ分）なので
　\(2\times \triangle \mathrm{PAB}=2\times 3=6\)
でも求まります。

他の関数との交点とで囲む面積は学年が進んでからで良いですが、
１つだけ反比例が持っている面積の性質をお伝えしておきます。

つねに同じ面積になる反比例の性質

関数は反比例なら何でも良いですが、問題で使った関数を使いましょう。

反比例 \(\displaystyle y=\frac{6}{x}\) 上の点P \((\,2\,,\,3\,)\) から、
軸に平行線を引いてできる長方形の面積は
　\(\mathrm{PA}\times \mathrm{PB}= \color{magenta}{6}\)
でした。

では、関数上の別の点 \((\,1\,,\,6\,)\) から、
軸に平行線を引いてできる長方形の面積を求めてみましょう。

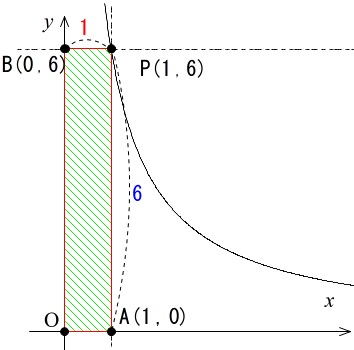
　\((面積)=\mathrm{PA}\times \mathrm{PB}=6\times 1=\color{magenta}{6}\)

です。
この値は先ほどの面積と同じです。

これはたまたまではありません。
同じ反比例のグラフ上の点であればすべて長方形の面積が同じになります。

理由は簡単で、反比例の関数は、
　
　\(\displaystyle \color{red}{y=\frac{a}{x}}\) であり、\(\color{red}{xy=a}\)

でもあります。

これは \(x\) 座標と \(y\) 座標をかけると一定、ということなので、
反比例のグラフ上のすべての点で \(x\) 座標と \(y\) 座標の積が一定、
つまり、
　グラフ上の点から軸に平行な線を引いてできる長方形の面積は常に一定
になるのです。

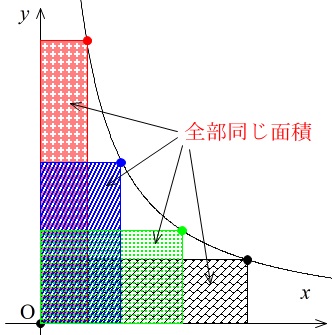
文字を使って証明しておいても良いのですが、
事実だけでも知っておくと便利なこともあるので覚えておくと良いですよ。