奈良県公立高校入試問題2019年(平成31年)度の数学の解説【後半】

2019年(平成31年)度に奈良県で行われた公立高校入試数学問題の解説後半です。
第3問は反比例のグラフの性質と面積を等しく分ける座標を求める問題、第4問は平行四辺形の折り返し問題です。
作図や相似の証明は簡単ですが、線分比の利用になれていないと線分の長さと面積までがわかりにくかったかもしれません。

問題は奈良県も公開してくれています。

⇒　2019年奈良県公立高校入試の数学問題

　\(\color{black}{\fbox{　3　}}\)

関数\(\displaystyle \,y=\frac{\color{red}{a}}{x}\,\)は反比例で、グラフは原点対称の双曲線になります。

また、反比例を表す関数は

　\(xy=\color{red}{a}\)

とも表せるので、どちらの形でも覚えておきましょう。

先ずは比例定数\(\,\color{red}{a}\,\)を決めて座標の\(\,\mathrm{A,B}\,\)を書き込みます。

(1)
曲線上の点が与えられています。

　\(\,\mathrm{A\,(\,2\,,\,3\,)}\,\)
　\(\,\mathrm{B\,(\,-2\,,\,-3\,)}\,\)

どちらを代入しても\(\,\color{red}{a}\,\)は同じ値で求まります。
\(\,\mathrm{A}\,\)を代入して、

　\(\begin{eqnarray}\displaystyle
(3)&=&\frac{a}{(2)}\\
6&=&\color{red}{a}
\end{eqnarray}\)

答え　\(\,a=\underline{　6　}\,\)

(2)
反比例を表す関数は

　\(xy=a\)

でもあるので、

　\(xy=6\)

これは\(\,x\,\)と\(\,y\,\)の積が一定であることを意味しています。

答え　\(\,　ウ　\,\)

グラフでいうと曲線上の点と軸に平行な直線と軸で作る長方形の面積が一定、
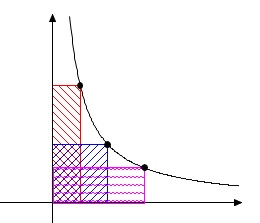（\(\color{red}{\fbox{赤色}}\)、\(\color{blue}{\fbox{青色}}\)、\(\color{magenta}{\fbox{桃色}}\)の長方形の面積は一定です。）
ということですが今は関係ありませんね。笑
(3)
曲線上の点\(\,\mathrm{P}\,\)の座標が\(\,(\,6\,,\,1\,)\,\)のときを考えます。

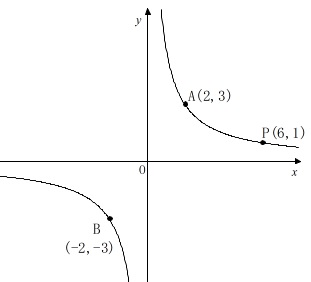
①
1つの点で\(\,x\,\)座標も\(\,y\,\)座標も整数の座標を格子点と呼ぶことにしましょう。
例えば、\(\,(1,1)\,\)や\(\,(4,1)\,\)などは格子点です。

\(\,\mathrm{△OAP}\,\)内部と周上にある格子点の個数を求めます。

格子点の数を求めるときはできるだけ具体的に格子点に\(\,●\,\)を書き込むことです。
注意するのは境界となる直線上の点なので、直線を具体的に求めておくと分かり易くなります。

直線\(\,\mathrm{OA}\,\)は
　\(\,(0,0)\,\)　\(\,(2,3)\,\)
を通る直線なので
　\(\displaystyle \,y=\frac{3}{2}x\,\)

直線\(\,\mathrm{OP}\,\)は
　\(\,(0,0)\,\)　\(\,(6,1)\,\)
を通る直線なので
　\(\displaystyle y=\frac{1}{6}x\)

直線\(\,\mathrm{AP}\,\)は
　\(\,(2,3)\,\)　\(\,(6,1)\,\)
を通る直線なので
　\(\displaystyle \,y=-\frac{1}{2}x+4\,\)

これらの直線を見ながら格子点を書き込むと、

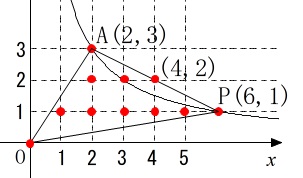
双曲線はここでは関係ありません。

直線\(\,\mathrm{AP}\,\)上に1つ格子点があることに注意すれば、
他は明らかに上下関係は見て取れますね。

答え　\(\,\underline{　11　}　(個)\,\)

②
直線\(\,\mathrm{BP}\,\)と\(\,x\,\)軸との交点を\(\,\mathrm{C}\,\)、
線分\(\,\mathrm{AB}\,\)上の点を\(\,\mathrm{D}\,\)とし、
\(\,\mathrm{△BCD}\,\)と四角形\(\,\mathrm{ADCP}\,\)の面積が等しくなるときの\(\,\mathrm{D}\,\)の座標を求めます。
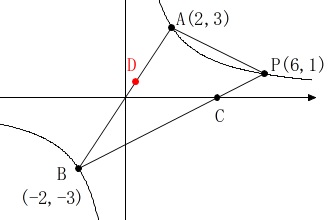四角形が平行四辺形の場合は対角線の交点を通るとき\(\,2\,\)等分しますが、三角形の場合は決まっていません。

\(\,\mathrm{△BCD}\,\)と四角形\(\,\mathrm{ADCP}\,\)の面積が等しくなるのは、
\(\,\mathrm{△BCD}\,\)の面積が\(\,\mathrm{△ABP}\,\)の面積の半分になるときです。

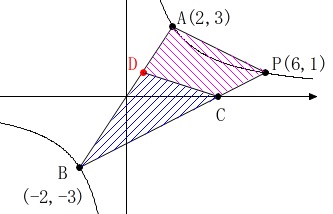
\(\,\mathrm{C}\,\)の座標は分かり易いので直線\(\,\mathrm{AB}\,\)の式を出して座標を設定しても良いですが、
少しややこしくなるので具体的な面積計算で行きます。

どちらにしても\(\,\mathrm{C}\,\)の座標を求めるのに直線\(\,\mathrm{BP}\,\)の式は必要なので先に出しておきましょう。

\(\,\mathrm{B,P}\,\)を通る直線は
　\(\,(\,-2\,,\,-3\,)\,\)
　\(\,(\hspace{8pt}6\,,\hspace{8pt}1\,)\,\)
から傾きが、

　\(\displaystyle \frac{1-(-3)}{6-(-2)}=\frac{1}{2}\)

なので、\(\,(\,-2\,,\,-3\,)\,\)を通ることから

　\(\displaystyle \,y=\frac{1}{2}x+2\,\)

\(\,\mathrm{C}\,\)は\(\,y=0\,\)（\(\,x\,\)軸）のときなので、

　\(\begin{eqnarray}
0&=&\frac{1}{2}x-2\\
x&=&4
\end{eqnarray}\)

よって、\(\,\mathrm{C\,(\,4\,,\,0\,)}\,\)

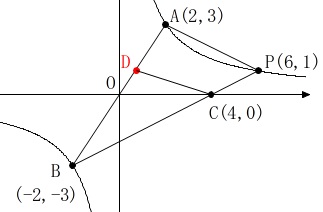三角形を\(\,2\,\)等分するので先に\(\,\mathrm{△ABP}\,\)の面積を求めましょう。

点\(\,\mathrm{A}\,\)から\(\,y\,\)軸に平行線を引いて、\(\,\mathrm{BP}\,\)との交点を\(\,\mathrm{E}\,\)として\(\,\mathrm{AE}\,\)を底辺とする三角形2つの面積として求めるのが普通でしょう。
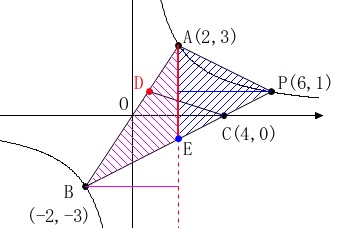直線\(\,\mathrm{BP}\,\)において\(\,x=2\,\)とすると、

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 2-2\\
&=&-1
\end{eqnarray}\)

このことから\(\,\mathrm{E}\,\)の座標は

　\(\mathrm{E}\,(\,2\,,\,-1\,)\)

だから底辺とする\(\,\mathrm{AE}\,\)の長さは\(\,y\,\)座標の差なので

　\(\mathrm{AE}=3-(-1)=\color{red}{4}\)

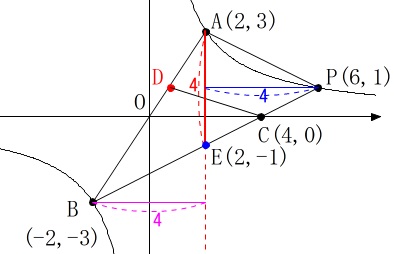2つの三角形の高さは\(\,x\,\)座標の差なので、

　\(\begin{eqnarray}
\mathrm{△ABP}&=&\mathrm{\color{blue}{△APE}+\color{magenta}{△ABE}}\\
&=&\color{blue}{\frac{1}{2}\times 4\times 4}+\color{magenta}{\frac{1}{2}\times 4\times 4}\\
&=&\color{blue}{8}+\color{magenta}{8}\\
&=&16
\end{eqnarray}\)

つまり、\(\,\mathrm{△BCD}\,\)の面積が\(\,\color{red}{8}\,\)となれば\(\,2\,\)等分します。

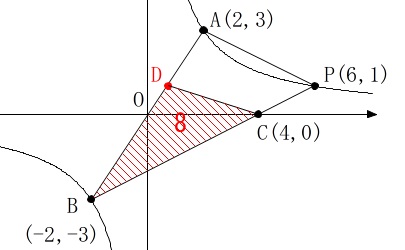
　\(\mathrm{△BCD=△OBC+△OCD}\)

で底辺は\(\,\mathrm{OC=4}\,\)、高さを\(\,\mathrm{B}\,\)の\(\,y\,\)座標の絶対値とすると

　\(\begin{eqnarray}
\mathrm{△OBC}&=&\frac{1}{2}\times 4\times 3\\
&=&6
\end{eqnarray}\)

このことから\(\,\mathrm{△OCD}\,\)の面積が\(\,2\,\)になれば良いことになります。

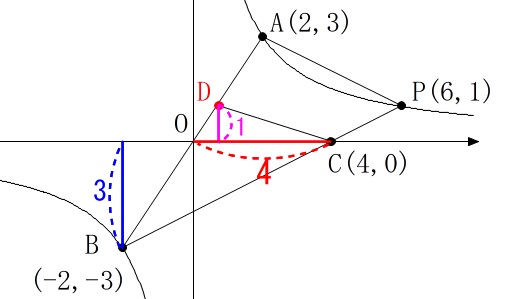
底辺は\(\,\mathrm{OC=4}\,\)で同じなので高さが\(\,\mathrm{D}\,\)の\(\,y\,\)座標で、
\(\,y=1\,\)のときの直線\(\,\mathrm{AB}\,\)上の\(\,\mathrm{D}\,\)を求めれば良いのです。

直線\(\,\mathrm{AB}\,\)の式は\(\displaystyle \,y=\frac{3}{2}x\,\)なので、

　\(\begin{eqnarray}
1&=&\frac{3}{2}x\\
x&=&\frac{2}{3}
\end{eqnarray}\)

よって\(\,\mathrm{D}\,\)の座標は

　\(\displaystyle \,\underline{　\left(\,\frac{2}{3}\,,\,1\,\right)　}\,\)

\(\,\mathrm{△ABP}\,\)の面積を求めるときですが、

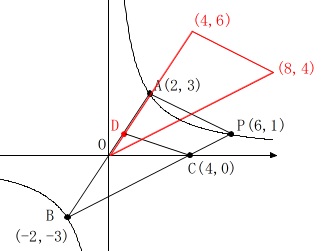
『覚え太郎』会員は
　\(\begin{eqnarray}
\mathrm{△ABP}&=&\left|\frac{4\times 4-6\times 8}{2}\right|\\
&=&\left|\frac{16-48}{2}\right|\\
&=&\left|\frac{-32}{2}\right|\\
&=&16
\end{eqnarray}\)

として良いですよ。
途中の考え方を書けとは書いていないので、採点者には分かりません。笑

\(\color{black}{\fbox{　4　}}\)

平行四辺形\(\,\mathrm{ABCD}\,\)があります。

条件を図に書き込みます。

　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{BC=12}\,\)
　\(\displaystyle \,\mathrm{ED=\frac{1}{2}DC}\,\)
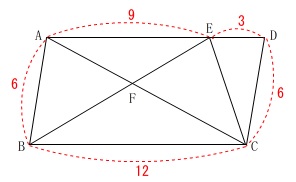平行四辺形なので角度についてもいろいろと言えますが、問題に合わせて進めていくということで長さだけを書き込んでおきました。

(1)
点\(\,\mathrm{E}\,\)を作図します。

長さが\(\,\mathrm{DC}\,\)の半分なので\(\,3\,\)と分かりますが、
作図で考えると\(\,\mathrm{DC}\,\)の中点を探せば良いことになります。

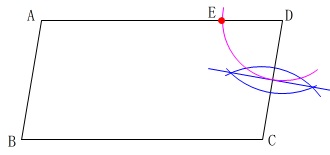
線分\(\,\mathrm{DC}\,\)の垂直二等分線を引いて中点を探し、
同じ半径の円を描いて、\(\,\mathrm{AD}\,\)との交点を\(\,\mathrm{E}\,\)とすれば良いだけです。

(2)
\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△EDC}\,\)を証明します。

図形の証明のポイントになるのは、図の中で証明を終わらせておくことです。
図の中で証明できていないことを文章にできるわけがありません。
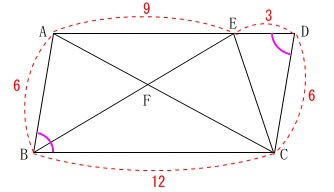平行四辺形の対角は等しいので証明は終わっています。

（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△EDC}\,\)において
平行四辺形の対辺は等しいので
　\(\,\mathrm{AB=DC=6}\,\)　･･･①
また、
　\(\displaystyle \,\mathrm{ED=\frac{1}{2}DC=3}\,\)　･･･②
\(\,\mathrm{BC=12}\,\)であることと①②から
　\(\,\mathrm{AB:ED=6:3=2:1}\,\)　･･･③
　\(\,\mathrm{BC:DC=12:6=2:1}\,\)　･･･④
さらに、　平行四辺形の対角は等しいから、
　\(\mathrm{∠ABC=∠EDC}\)　･･･⑤
③④⑤より
　\(\,2\,\)組の辺の比とその間の角がそれぞれ等しい
ので
　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△EDC}\,\)
（終わり）

（3)
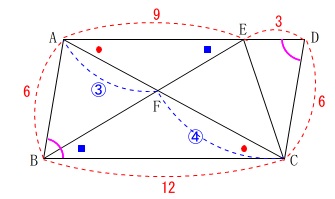
線分\(\,\mathrm{CE}\,\)と線分\(\,\mathrm{AF}\,\)の長さを比較します。

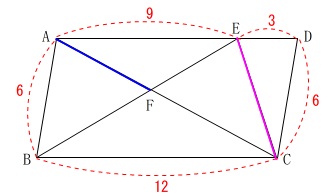
与えられた条件では平行四辺形が定まらないので具体的には長さは求まりません。

しかし、相似な三角形が(2)で示したもの以外にもあるので利用できます。
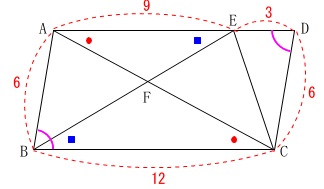平行線の錯角が等しいことから、

　\(\,\mathrm{△FAE}\,\)　∽　\(\,\mathrm{△FCB}\,\)
だから
　\(\,\mathrm{FA:FC=9:12=3:4}\,\)

また、

　\(\,\mathrm{△ABC}\,\)　∽　\(\,\mathrm{△EDC}\,\)
なので、
　\(\,\mathrm{AC：EC=2:1}\,\)

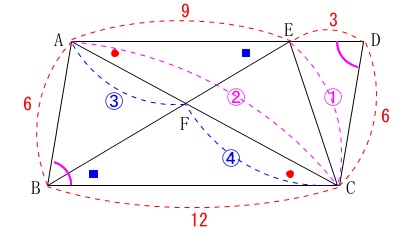
このとき、\(\,\mathrm{CE＝1}\,\)とすると
　\(\displaystyle \,\mathrm{AF=2\times \frac{3}{7}=\frac{6}{7}}\,\)

よって、

　\(\displaystyle \,\mathrm{CE:AF=1:\frac{6}{7}}\,\)

なので

　\(\displaystyle \mathrm{AF=\frac{7}{6}CE}\)

答え　\(\displaystyle \underline{　\frac{7}{6}　}\)　倍

(4)
　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{BC=12}\,\)
に
　\(\,\mathrm{AC=12}\,\)
が条件に加わります。
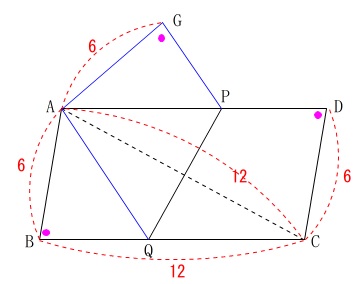頂点\(\,\mathrm{C}\,\)が\(\,\mathrm{A}\,\)に重なるように折り返すので、対称の軸は\(\,\mathrm{PQ}\,\)です。

このとき四角形\(\,\mathrm{AQPG}\,\)の面積を求めます。
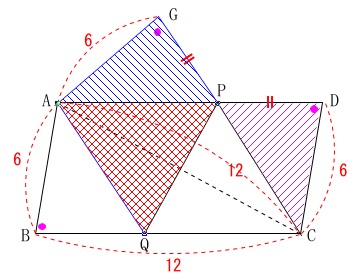面積の出し方はいろいろとありますが、合同を使って簡単に求める方法だけ紹介しておきます。

折り返しの性質から

　\(\,\mathrm{△AGP}\,\)　≡　\(\,\mathrm{△CDP}\,\)

なので、

　\(\begin{eqnarray}\displaystyle
四角形\mathrm{AQPG}&=&\mathrm{\color{blue}{△AGP}+\color{red}{△AQP}}\\
&=&\mathrm{\color{magenta}{△PCD}}+\mathrm{\color{red}{△AQP}}\\
&=&\frac{1}{2}\times (四角形\mathrm{AQPG})
\end{eqnarray}\)

高さは共通で、底辺の和を考えると、

　\(\,\mathrm{\color{red}{AP}+\color{magenta}{PD}=AD}\,\)

なので平行四辺形の面積の半分になります。

\(\,\mathrm{AB}\,\)に平行な線分で切るとそれぞれの平行四辺形が2等分されているので直感的にも分かるでしょう。

ということで平行四辺形\(\,\mathrm{ABCD}\,\)の面積を求めるための高さが必要になります。
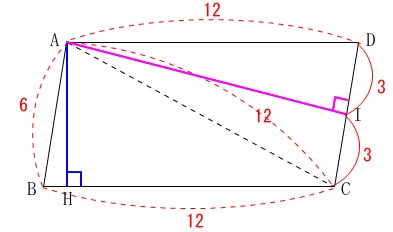\(\,\mathrm{△ABC}\,\)は二等辺三角形で\(\,\mathrm{AH}\,\)を直接求めることもできるのですが、

　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△ACD}\,\)は面積は同じです。

つまり、平行四辺形\(\,\mathrm{ABCD}\,\)の半分になるので、

　\(\,\mathrm{四角形AQPG=\color{blue}{△ABC}=\color{magenta}{△ACD}}\,\)

です。

なので分かり易い\(\,\mathrm{\color{magenta}{△ACD}}\,\)の面積を求めます。

二等辺三角形の頂角から底辺に垂線を引くと底辺の中点に下りるので、

　\(\mathrm{CI=\color{red}{ID}=\color{red}{3}}\)

\(\,\mathrm{△AID}\,\)に三平方の定理を用いて、

　\(\begin{eqnarray}
\mathrm{AI^2+\color{red}{ID}^2}&=&\,\mathrm{AD^2}\,\\
\mathrm{AI^2}+(\color{red}{3}^2)&=&(12)^2\\
\mathrm{AI^2}+9&=&144\\
\mathrm{AI^2}&=&144-9\\
&=&135\\
\mathrm{AI}&=&3\sqrt{15}　(\,\mathrm{AI}\,＞\,0\,)
\end{eqnarray}\)

よって、求める四角形の面積は

　\(\begin{eqnarray}\displaystyle
四角形\mathrm{AQPG}&=&\mathrm{△ACD}\\
&=&\frac{1}{2}\times \mathrm{DC}\times \mathrm{AI}\\
&=&\frac{1}{2}\times 6\times 3\sqrt{15}\\
&=&\underline{　9\sqrt{15}　}　(\mathrm{cm^2})
\end{eqnarray}\)

長さを求めに行こうとして手を動かしているうちに、
分かることがいろいろと出てくるので方針が定まりにくいですが、

　最初から最後までいきなり解法が思いつくわけでは無い。

ということを解答にしてみました。

他にも

　ひし形
　合同な三角形
　
を利用して求めることもできます。
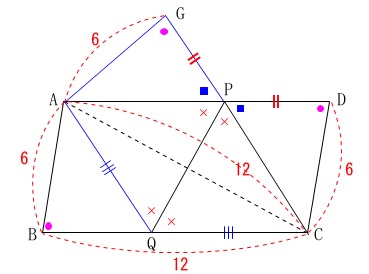折り返された辺と角は等しいことからいろいろなことが言えるので確認してみてください。