滋賀県で2018年(平成30年度)に行われた公立高校入試の数学問題の解説です。
大問は4つですが、第1問の小問集合で10問、後の大問は3問から4問となっていて問題数としては多くはありません。
ただ、後半の問題は配点が高いですが、ながめているだけでは答えは出ません。
どれだけ手を動かすかで差が出る問題となっています。
問題は滋賀県で公開してくれています。
基本確認の小問集合
\(\color{black}{\fbox{ 1 }}\)は正負の数、文字式の計算、方程式、無理数、円柱と球の体積、確率の基本確認です。
正の数負の数と文字式の計算と方程式
(1)
海面を基準に山の高さと湖の底との差を求めます。
海面の高さを\(\,0\,\)
比叡山の山頂を\(\,+848\,\)
琵琶湖の一番深い所を\(\,-19\,\)
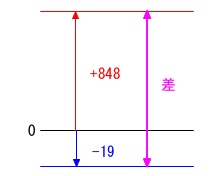単純に引き算すれば差が出ます。
\(\hspace{10pt}+848-(-19)\\
=848+19\\
=\underline{ 867 } (\,\mathrm{m}\,)\)
数直線で横に見ても良いですね。
(2)
\(\displaystyle \hspace{10pt}\frac{2}{3}a+\frac{1}{2}a\\
=\displaystyle \frac{4a+3a}{6}\\
=\displaystyle \underline{ \frac{7a}{6} }\)
分母を一つにして分子の計算に集中するとミスが減ります。
\(\displaystyle \hspace{10pt}\frac{7\color{red}{a}}{6}=\frac{7}{6}\color{red}{a}\)
としても同じ意味です。
\(\,a\,\)は分子にあります。
(3)
連立方程式を解くときの基本的な方針は一文字消去です。
\( \begin{cases}
\hspace{7pt} 2x+y=11 ･･･①\\ \\
\hspace{7pt} 8x-3y=9 ･･･②
\end{cases}\)
どちらの文字を消去しても良いです。
①の\(\,2x\,\)を移項して代入法でも良いですが、加減法で進めます。
\(\,①\times 3+②\,\)によって\(\,y\,\)を消去します。
\(\hspace{14pt}6x+3y=33\\
\underline{+)\,8x-3y=\hspace{4pt}9}\\
\hspace{8pt}14x\hspace{22pt}=42\\
\hspace{39pt}x=3\)
①に代入して
\(\begin{eqnarray}
2\times (3)+y&=&11\\
6+y&=&11\\
y&=&11-6\\
&=&5
\end{eqnarray}\)
よって
\(\underline{ x=3\,,\,y=5 }\)
(4)
文字式でも単なる数値でも、割り算は逆数のかけ算です。
\(\hspace{10pt}(9a^2b-15a^3b)\div 3ab\\
\displaystyle =(9a^2b-15a^3b)\times \frac{1}{3ab}\\
\displaystyle =\frac{9a^2b}{3ab}-\frac{15a^3b}{3ab}\\
=\underline{ 3a-5a^2 }\)
もちろん、そのまま割ってもきれいに割り切れます。
\(\hspace{10pt}(9a^2b-15a^3b)\div 3ab\\
=\underline{ 3a-5a^2 }\)
ただ、分母が残るときのことを考えると、
いつも逆数のかけ算にしておく方が一つの方針で計算を進めることができます。
(5)
\(\,2\,\)次方程式を解きますが、方程式を解くときは左辺にすべての項を集めて右辺を\(\,0\,\)にすることが基本です。
それと、\(\,2\,\)次方程式を解くことと、\(\,2\,\)次方程式の解を求めることは同じことですよ。
\(\begin{eqnarray}
(x-3)(x-5)&=&-1\\
x^2-8x+15+1&=&0\\
x^2-8x+16&=&0\\
(x-4)^2&=&0\\
x&=&\underline{ 4 }
\end{eqnarray}\)
普通なら\(\,2\,\)次方程式の解は\(\,2\,\)個ありますが、ここでは「重解」なので一つです。
⇒ 方程式の解とは？2次方程式の係数と他の解を求める代入問題の解き方
関数の比例定数の決定と2点間の距離およびルートの性質
(6)
①\(\,y\,\)が\(\,x^2\,\)に比例する関数の比例定数を求め、\(\,2\,\)点間の距離を三平方の定理で求めます。
「\(y=ax^2\,\)が\(\,\mathrm{A\,(\,2\,,\,6\,)}\,\)を通る」
\(y=ax^2\,\)に\(\,(\,2\,,\,6\,)\,\)を代入するだけです。
\(\begin{eqnarray}
6&=&a\times (2^2)\\
6&=&4a\\
4a&=&6\\
a&=&\frac{6}{4}=\underline{ \frac{3}{2} }
\end{eqnarray}\)
②
原点\(\,\mathrm{O}\,(\,\color{red}{0}\,,\,\color{blue}{0}\,)\)
と
点\(\,\mathrm{A}\,(\,\color{red}{2}\,,\,\color{blue}{6}\,)\)
の\(\,2\,\)点間の距離です。
公式でももちろん良いですが、座標上では直角三角形を考え三平方の定理を利用することが元になっている公式ですね。
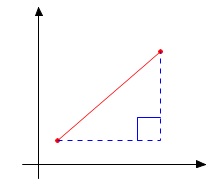
\(\begin{eqnarray}
\mathrm{OA^2}&=&(\color{red}{2}-\color{red}{0})^2+(\color{blue}{6}-\color{blue}{0})^2\\
&=&2^2+6^2\\
&=&4+36\\
&=&40\\
\mathrm{OA}&=&\pm 2\sqrt{10}\\
\end{eqnarray}\)
\(\,\mathrm{OA}\,\)は長さなので\(\,\mathrm{OA\,＞\,0}\,\)
\(\mathrm{OA}=\underline{ 2\sqrt{10 }}\)
(7)
ルートの付いた数が自然数になるには、
ルートの中が平方数
にならなければなりません。
\(\,24\,\)を素因数分解すると
\(2\underline{)\,24}\\
2\underline{)\,12}\\
2\underline{)\hspace{6pt}6}\\
\hspace{15pt}3\)
なのでルートの中だけを見ると
\(\hspace{10pt}24n\\
=\color{red}{2^2}\times \color{blue}{2\times 3\times n}\)
となっているので
\(\color{blue}{2\times 3}\)
の部分を
\(\color{red}{2^2\times 3^2}\)
とすれば良いので
\(n=2\times 3=\underline{ 6 }\)
\(\,24n\,\)を平方数にするのは\(\,n=6\,\)だけでは無く、
\(\,n=6k^2\,(\,k=1\,,\,2\,,\,3\,\cdots)\)
であれば平方数になりますが、
「もっとも小さいもの」
なので\(\,k=1\,\)のときの\(\,n=6\,\)が答えになります。
⇒ ルートのついた無理数を整数や自然数に変える方法と問題の解き方
球の体積と円柱の体積の比較と確率
(8)
半径\(\,r\,\)の半休と、底面の半径が\(\,r\,\)、高さが\(\,2r\,\)の円柱との体積の比較です。
それぞれの体積を\(\,r\,\)を用いて表し、割り算すれば良いだけです。
容器\(\,\mathrm{A}\,\)の半球の体積は
\(\hspace{10pt}\displaystyle \frac{4}{3}\pi r^3\times \frac{1}{2}\\
\displaystyle =\frac{2}{3}\pi\, r^3\)
容器\(\,\mathrm{B}\,\)の円柱の体積は
\(\hspace{10pt}\pi r^2\times 2r\\
=2\pi\, r^3\)
よって、容器\(\,\mathrm{B}\,\)には容器\(\,\mathrm{A}\,\)の
\(\hspace{10pt}\displaystyle 2\pi\,r^3\div \frac{2}{3}\pi\,r^3\\
\displaystyle =2\pi\,r^3 \times \frac{3}{2\pi\,r^3}\\
\displaystyle =\underline{ 3 } (杯分)\)
たまにどっちをどっちで割るかが分からなくなる、という人がいますが、
「\(\,6\,\)は\(\,2\,\)の何倍か？」
と聞かれれば
「\(6\div 2=3\)」
としますよね？
同じように
「容器\(\,\mathrm{B}\,\)は容器\(\,\mathrm{A}\,\)の何倍か？」
と単純な計算と同じ方法で割れば良いだけですよ。
普通の中学生では球の体積や表面積の公式を求めることはできませんので、
球の体積の求め方は公式を覚えるしか方法はありません。
(9)
\(\,1\,\)から\(\,5\,\)の数字を一回ずつ使って二桁の整数を作ります。
\(12\,,\,\color{red}{13}\,,\,14\,,\,15\)
\(21\,,\,\color{red}{23}\,,\,24\,,\,25\)
\(\color{red}{31}\,,\,32\,,\,34\,,\,35\)
\(\color{red}{41}\,,\,42\,,\,\color{red}{43}\,,\,45\)
\(51\,,\,52\,,\,\color{red}{53}\,,\,54\)
二桁の整数は\(\,20\,\)個できますがそのうち「素数」は赤字の\(\,6\,\)個なので求める確率は
\(\displaystyle \frac{6}{20}=\underline{ \frac{3}{10} }\)
⇒ 素数とは？素因数分解の方法と平方根の求め方(ルートの使い方準備)
素数については気をつけることがありますので確認しておいた方が良いですよ。
\(\color{black}{\fbox{ 1 }}\)の小問集合はここまでです。
次は規則性と文字式の問題ですが円周角についても聞かれます。
規則性と文字式による証明
九九の一の位の規則性
この問題は円周上に点を取って九九の答えの一の位を順にたどってできる形を見ます。
問題をながめていてもわかりにくいですが、問題に書いてある通り\(\,4\,\)の段と\(\,6\,\)の段は同じです。
\(\,1\,\)から\(\,6\,\)の段までの図は問題にあるので、\(\,7\,\)から\(\,9\,\)の段までの図を書けば見えてきます。
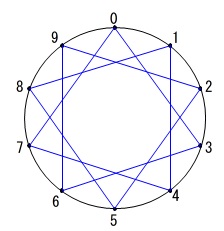
\(\,7\,\)の段の九九の答えは
\(\,\color{blue}{7} 1\color{blue}{4} 2\color{blue}{1} 2\color{blue}{8} 3\color{blue}{5} 4\color{blue}{2} 4\color{blue}{9} 5\color{blue}{6} 6\color{blue}{3}\,\)
これは\(\,3\,\)の段の九九の答えの一の位
\(\,\color{blue}{3} \color{blue}{6} 9 1\color{blue}{2} 1\color{blue}{5} 1\color{blue}{8} 2\color{blue}{1} 2\color{blue}{4} 2\color{blue}{7}\,\)
と逆の順になっていてできあがる形は同じです。
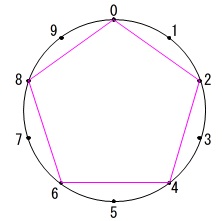
\(\,8\,\)の段の九九の答えは
\(\,\color{magenta}{8} 1\color{magenta}{6} 2\color{magenta}{4} 3\color{magenta}{2} 4\color{magenta}{0} 4\color{magenta}{8} 5\color{magenta}{6} 6\color{magenta}{4} 7\color{magenta}{2}\,\)
これは\(\,2\,\)の段の九九の答えの一の位
\(\,\color{magenta}{2} \color{magenta}{4} \color{magenta}{6} \color{magenta}{8} 1\color{magenta}{0} 1\color{magenta}{2} 1\color{magenta}{4} 1\color{magenta}{6} 1\color{magenta}{8}\,\)
と逆の順になっていてできあがる形は同じです。
すでに気がついていると思いますが、
足して\(\,10\,\)になる九九の答えの一の位は順序は逆になるけど同じ形になっています。
\(\,9\,\)の段も\(\,1\,\)の段の九九と同じ形になるか見ておきます。
\(\,9\,\)の段の九九の答えは
\(\,\color{red}{9} 1\color{red}{8} 2\color{red}{7} 3\color{red}{6} 4\color{red}{5} 5\color{red}{4} 6\color{red}{3} 7\color{red}{2} 8\color{red}{1}\,\)
\(\,1\,\)の段の九九の答えは
\(\,\color{red}{1} \color{red}{2} \color{red}{3} \color{red}{4} \color{red}{5} \color{red}{6} \color{red}{7} \color{red}{8} \color{red}{9}\,\)
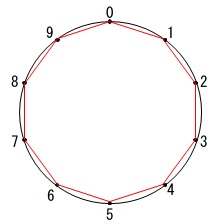同じ形です。
一の位の数が逆になることは数式で示すこともできますが長くなるのでここではやりません。笑
\(\,m\,\)の段と同じ形になる段の数は、
\(\,\underline{ 10-m }\,\)
図を横に並べると\(\,5\,\)の段を真ん中に対称に並んでいることに気がつきますね。
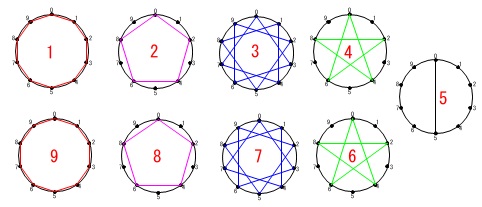
円周を等分したときの円周角
等しい大きさの円周角\(\,10\,\)個の和を求めることになります。
円周角を求めるには中心角から求める方が普通でしょう。
なので１つ分の中心角を求めましょう。
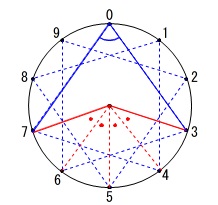点\(\,3\,\)と中心と点\(\,7\,\)とでできる中心角は、\(\,360°\,\)を\(\,10\,\)等分した4つ分なので、
\(\hspace{10pt}360^{\circ}\div 10\times 4\\
=\color{red}{144^{\circ}}\)
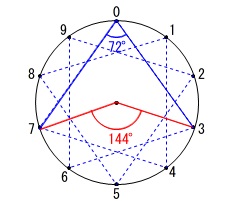
このときの円周角は半分の\(\,\color{blue}{72°}\,\)になるので求める\(\,10\,\)個の角の和は
\(\hspace{10pt}72^{\circ}\times 10\\
=\underline{ 720^{\circ} }\)
中心角ではなく、周に対する円周角が\(\,180°\,\)として、
\(\hspace{10pt}\displaystyle 180^{\circ}\times \frac{4}{10}\times 10\\
=\underline{ 720^{\circ} }\)
『覚え太郎』会員はこちらで求めたと思いますが、どちらでも良いですよ。
規則性と文字式の利用
(3)
これは表を\(\,n\,\)で表せばすぐに分かる規則性問題なので簡単に済ませます。
\(\,1\,\)から\(\,n\,\)までの数字で九九を計算する表で、
四すみの数をたすとどうなるか\(\,n\,\)を用いて表します。
四すみの右下は平方数で\(\,n^2\,\)なので
\(\begin{array}{|c|c|c|c|c|} \hline
\color{red}{1} & 2 & 3 & \cdots & \color{red}{n} \\ \hline
2 & 4 & 6 & & 2n \\ \hline
3 & 6 & 9 & & 3n \\ \hline
\cdots & & & & \\ \hline
\color{red}{n} & 2n & 3n & & \color{red}{n^2} \\ \hline
\end{array}\)
よって、四すみの数の和は
\(\hspace{10pt}\color{red}{1}+\color{red}{n}+\color{red}{n}+\color{red}{n^2}\\
=n^2+2n+1\\
=\underline{ (n+1)^2 }\)
(4)
これも左上の数字を左から\(\,x\,\)番目、上から\(\,y\,\)番目として4つの数を表せば簡単に説明できます。
「
左上の数字は左から\(\,x\,\)番目、上から\(\,y\,\)番目なので、
その九九の答えは\(\,xy\,\)
左上の右横の数は、左から\(\,x+1\,\)番目、上から\(\,y\,\)番目なので
その九九の答えは\(\,(x+1)y\,\)
左上の下の数は、左から\(\,x\,\)番目、上から\(\,y+1\,\)番目なので
その九九の答えは\(\,x(y+1)\,\)
右下の数は、左から\(\,x+1\,\)番目、上から\(\,y+1\,\)番目なので
その九九の答えは\(\,(x+1)(y+1)\,\)
と表すことができます。
\(\begin{array}{|c|c|} \hline
xy & (x+1)y \\ \hline
x(y+1) & (x+1)(y+1) \\ \hline
\end{array}\)
なので４つの数の和は
\(\hspace{10pt}xy+(x+1)y+x(y+1)+(x+1)(y+1)\\
=xy+xy+y+xy+x+xy+x+y+1\\
=4xy+2x+2y+1\\
=2(2xy+x+y)+1\)
このとき\(\,2xy+x+y\,\)は整数なので
\(2(2xy+x+y)\,\)は偶数
よって4つの数の和は奇数である。」
と書いておけば十分でしょう。
文字を使って表にすればすぐに出ますが計算を進めないと
偶数＋奇数＝奇数
の形に持って行けないので手を動かさないと大きな配点だけに差がつきますね。
\(\color{black}{\fbox{ 2 }}\)はここまでです。
⇒ 2018(平成30年度)の滋賀県公立高校入試問題数学の解説【後半】
\(\color{black}{\fbox{ 3 }}\)は図形の移動と面積の変化
\(\color{black}{\fbox{ 4 }}\)は正方形の折り返しによる角度と合同の証明問題です。
円の中心の作図はよく見ておいた方が良いです。
更新はこちらで確認できます。
全国の公立入試の多くで折り返し問題は出ていますので確認しておくと良いですね。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
