2018年(平成30年度)に滋賀県で行われた公立高校入試の数学問題の後半の解説です。
第3問の図形の移動と面積の変化、第4問は正方形の折り返し問題です。
第3問は動点問題と同じように各場面にそれぞれの図を書くことと、
第4問の折り返しは折り返しの軸に対して対称になる線分や角度をしっかり見てとることがポイントです。
問題は滋賀県で公開してくれています。
図形の移動と重なる面積
\(\color{black}{\fbox{ 3 }}\)は図形の移動と長さや面積の変化の問題です。
動点問題と同じように変化のある点を拾い出し、図を書いて考えることがポイントになります。
同じ形の扉なので分かり易いですが、問題の図は扉の影になる部分を黒塗りされているので長さを書き込んだとき見にくいです。笑
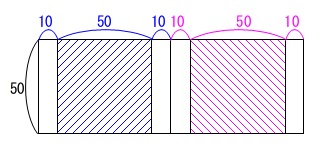 扉で無くても同じなので窓ガラスがある部分だけを抜き出して説明します。
扉で無くても同じなので窓ガラスがある部分だけを抜き出して説明します。
色つきの斜線部分が向こう側が見える範囲です。
問題全体を場合分けしておくと、
①窓の部分が2つに分けられているとき
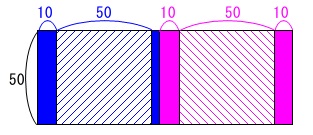
②窓の部分が3つに分けられているとき
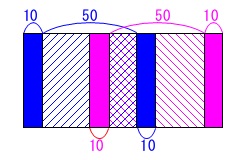
③窓の部分が1つになるとき
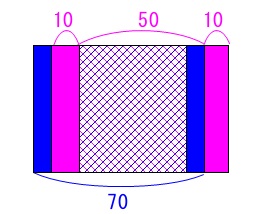
ということが分かれば\(\,\mathrm{P,Q,R}\,\)はあまり気にしなくて大丈夫です。
間隔が等分されるときの長さ
(1)②の状態で3つの窓ガラス部分が等しくなるときです。
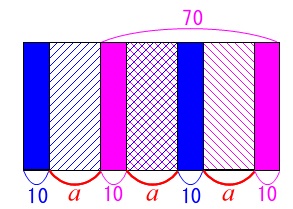
 全体で見るとややこしいですが、扉一枚で見るとわかりやすくなります。
全体で見るとややこしいですが、扉一枚で見るとわかりやすくなります。
扉一枚の横幅は\(\,70\,\)なので
\(\begin{eqnarray}
30+2\color{red}{a}&=&\color{magenta}{70}\\
2a&=&70-30\\
&=&40\\
a&=&\underline{ 20 } (\,\mathrm{cm}\,)
\end{eqnarray}\)
重なりと面積の関係
(2)②の状態、つまり窓ガラス部分が3つに分かれるときです。
左の扉が\(\,\mathrm{20\,cm}\,\)動いたときまでは窓ガラス分は2つです。
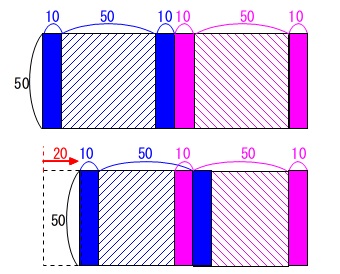 この後向こう側が見える面積は、真ん中の部分\(\,\mathrm{Q}\,\)で重なりが大きくなるので減っていきます。
この後向こう側が見える面積は、真ん中の部分\(\,\mathrm{Q}\,\)で重なりが大きくなるので減っていきます。
\(\,\mathrm{20\,cm}\,\)動いたときの面積は
\(\hspace{10pt}40\times 50\times 2\\
=4000\)
ここから動けばその分面積が減ります。
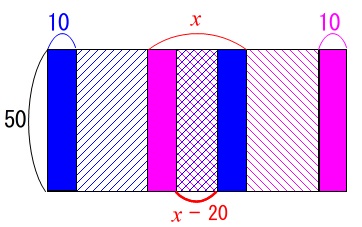 \(\,x\,\)動いたときの窓ガラス\(\,\mathrm{Q}\,\)の重なりの幅は\(\,x-20\,\)なので減る面積は
\(\,x\,\)動いたときの窓ガラス\(\,\mathrm{Q}\,\)の重なりの幅は\(\,x-20\,\)なので減る面積は
\(\hspace{10pt}50\times (x-20)\\
=50x-1000\)
これを\(\,4000\,\)から引いて求める面積\(\,y\,\)と動いた\(\,x\,\)との関係は
\(\begin{eqnarray}
y&=&4000-(50x-1000)\\
&=&5000-50x
\end{eqnarray}\)
②の状態は\(\,\mathrm{60\,cm}\,\)動くまで続くので、
\(\,20\,<\,x\,<\,60\,\)の範囲で面積は傾きが負の\(\,1\,\)次関数として減ることになります。
つまり
②の状態で面積の関係式は\(\,1\,\)次関数で
\(\,y=-50x+5000\,\)
となり、扉が動くとは面積は減る。
というのがこの問題の答えになりますね。
移動する図形と重なりの面積の最小値
(3)
扉が移動して、①の状態から③の状態に変化するまでには、
向こう側が全部見える状態が\(\,\mathrm{10\,cm}\,\)続き
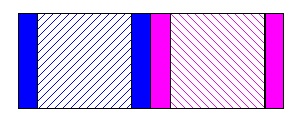 それから扉のガラスの周りの縁の部分がガラス部分をかくして減る状態になります。
それから扉のガラスの周りの縁の部分がガラス部分をかくして減る状態になります。
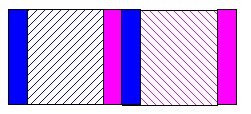 その後あと②の状態になり、
その後あと②の状態になり、
 このときは扉の縁の部分は一定なので面積は変化しないように見えますが、
このときは扉の縁の部分は一定なので面積は変化しないように見えますが、
(2)で説明した通り向こう側が見える面積はガラスの重なり分減ります。
次に、向こう側が見える部分が1つになる③の状態になります。
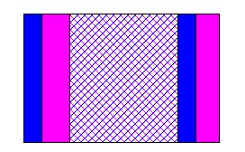 この③のときは扉の縁の重なり分が多くなる分、向こう側が見える部分は増えます。
この③のときは扉の縁の重なり分が多くなる分、向こう側が見える部分は増えます。
つまり、②の状態と③の状態のちょうど境目になるとき向こうが見える部分の面積は最小になります。

\(\hspace{10pt}40\times 50\\
=\underline{ 2000 } (\,\mathrm{cm^2}\,)\)
このとき扉は\(\,\mathrm{60\,cm\,}\,\)動いた状態なので、
(2)の関係式に\(\,x=60\,\)を代入して
\(\begin{eqnarray}
y&=&-50\times (60)+5000\\
&=&-3000+5000\\
&=&\underline{ 2000 }
\end{eqnarray}\)
としても同じ値になります。
移動し始め\(\,\mathrm{10cm}\,\)までの面積の変化の無い部分も含めて、
①②③の状態を\(\,x,y\,\)の関係式にしてグラフにすると分かりますが3つの直線はつながります。
そのグラフの一番下になる\(\,y\,\)座標が面積が最も小さくなる値です。
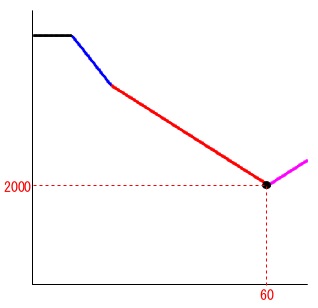
すべての状態を関数にすればすべての状態が変わりますが、この問題では必要無いようです。
ただし、(2)は関係式を出して、「傾きが負の\(\,1\,\)次関数なので減少する」、と理由をつけないと答えにくい問題ですね。
ちなみに関係式は
\(0≦x≦10\) で \(y=5000\)
\(10≦x≦20\) で \(y=-100x+6000\)
\(20≦x≦60\) で \(y=-50x+5000\)
\(60≦x≦70\) で \(y=50x-1000\)
となっています。
\(\color{black}{\fbox{ 3 }}\)は以上です。
動点問題や図形が移動する問題に限った話ではありませんが、
1つひとつ違う場面で図を書いて考えないとつながりませんよ。
次の\(\color{black}{\fbox{ 4 }}\)もその1つです。
正方形の折り返し
\(\color{black}{\fbox{ 4 }}\)の図形問題は与えられた図は見やすいですが、
問題の条件をよく読み、順番に書き込むことをしないと最後まではたどり着けません。
長さは1つも与えられていないので、正方形という条件と折り返した図形の性質のみで考えなくてはなりませんよ。
※
逆に長さは無くても一般的に成り立つのであれば、特定の長さを自分で決めても成り立つということですが、長さを特定せずに一般的に説明していきます。
折り返したとき等しい角と辺
(1)
折り返した図形では、
折り返した角度や辺は、折り返された角や辺と等しい
という性質を使います。
日本語で見るとわかりにくいかもしれませんが図で見るとすぐに分かります。
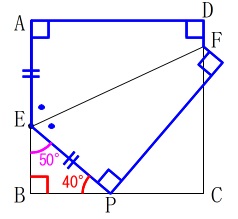 等しい角はたくさんありますが、
等しい角はたくさんありますが、
\(\mathrm{∠AEF=∠PEF}\)
だけで答えは出ます。
問題の条件にある\(\,∠\mathrm{BPE}=40^{\circ}\,\)から
\(∠\mathrm{BEP}=50^{\circ}\)
なので
\(\begin{eqnarray}
∠\mathrm{AEP}&=&180^{\circ}-50^{\circ}\\
&=&130^{\circ}
\end{eqnarray}\)
よって
\(\begin{eqnarray}
∠\mathrm{FEP}&=&130^{\circ}\div 2\\
&=&\underline{ 65^{\circ} }
\end{eqnarray}\)
差がつきやすい問題ですがここまでは確実にとっておきたいですね。
中心角の作図方法
(2)
\(\,\mathrm{∠PQG}\,\)が\(\,\mathrm{∠PHG}\,\)の②倍になる\(\,\mathrm{Q}\,\)を作図します。
\(\,\mathrm{P}\,\)は(1)で\(\,\mathrm{EF}\,\)を軸に折り返した\(\,\mathrm{A}\,\)が\(\,\mathrm{BC}\,\)上に重なる点です。
ここまででもややこしく感じますが、\(\,\mathrm{D}\,\)を\(\,\mathrm{P}\,\)に重なるように折り返したときの軸が\(\,\mathrm{GH}\,\)です。

中心角が円周角の\(\,2\,\)倍になることから、円の中心が\(\,\mathrm{Q}\,\)になることに気がつけば簡単に作図できます。
円の中心は1つの弦の垂直二等分線上にあります。
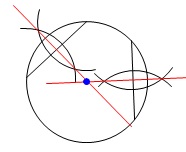 他の弦の垂直二等分線との交点を円の中心と決めることができますがここでは必要ありません。
他の弦の垂直二等分線との交点を円の中心と決めることができますがここでは必要ありません。
\(\,\mathrm{GH}\,\)上に中心\(\,\mathrm{Q}\,\)を作図することになるので、
1つの弦の垂直二等分線と\(\,\mathrm{GH}\,\)の交点が\(\,\mathrm{R}\,\)です。
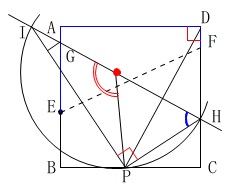 直線\(\,\mathrm{AH}\,\)で直角三角形\(\,\mathrm{IPH}\,\)を作り、
直線\(\,\mathrm{AH}\,\)で直角三角形\(\,\mathrm{IPH}\,\)を作り、
\(\,\mathrm{IP}\,\)の垂直二等分線と\(\,\mathrm{PH}\,\)の垂直二等分線との交点でも良いですが、
\(\,\mathrm{△IPH}\,\)を作る必要も無く、
\(\,\mathrm{PH}\,\)の垂直二等分線と\(\,\mathrm{GH}\,\)の交点が\(\,\mathrm{R}\,\)です。
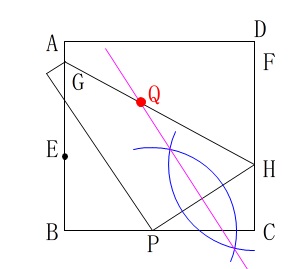
この垂直二等分線上に円の中心があるということは、(3)を考える上で重要なポイントになるのかな?笑
(2)においては、角度が\(\,2\,\)倍ということから、
円周角と中心角の関係
に気がつけば作図自体は簡単で、配点が\(\,7\,\)点は大きいですね。
合同の証明は図の中で完成させるのが基本
(3)
三角形の合同の証明です。
合同や相似の証明は図の中で示せていないと文章にすることはできません。
ただ、この問題は条件をつなぎ合わせる応用問題ですので簡単では無かったでしょう。
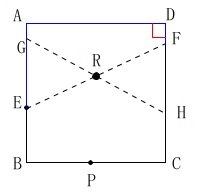 \(\,\mathrm{A}\,\)を\(\,\mathrm{P}\,\)に重ねたときの折り目が\(\,\mathrm{EF}\,\)です。
\(\,\mathrm{A}\,\)を\(\,\mathrm{P}\,\)に重ねたときの折り目が\(\,\mathrm{EF}\,\)です。
\(\,\mathrm{D}\,\)を\(\,\mathrm{P}\,\)に重ねたときの折り目が\(\,\mathrm{GH}\,\)です。
つまり、
\(\,\mathrm{EF}\,\)は線分\(\,\mathrm{AP}\,\)の垂直二等分線
\(\,\mathrm{GH}\,\)は線分\(\,\mathrm{DP}\,\)の垂直二等分線
になっているので、
点\(\,\mathrm{R}\,\)は\(\,\mathrm{△APD}\,\)の外接円の中心です。
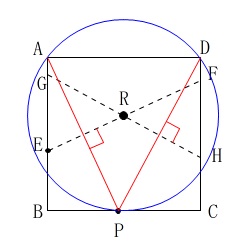 このとき、\(\,\mathrm{DR}\,\)は円の半径で、
このとき、\(\,\mathrm{DR}\,\)は円の半径で、
\(∠\mathrm{SAD}=90^{\circ}\)
であることから\(\,\mathrm{DS}\,\)は円の直径です。
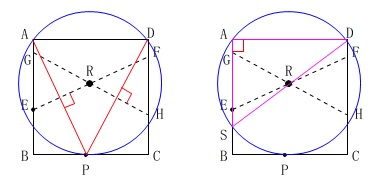 四角形\(\,\mathrm{ABCD}\,\)は正方形なので、
四角形\(\,\mathrm{ABCD}\,\)は正方形なので、
\(\,\mathrm{AB}\,/\!/\,\mathrm{DC}\,\)
だから錯角は等しくなるので
\(\mathrm{\color{blue}{∠RES}=\color{blue}{∠RFD}}\)
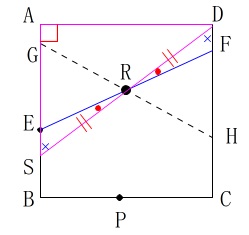 よって対頂角が等しいことも加えて合同が言えます。
よって対頂角が等しいことも加えて合同が言えます。
(錯角2つでも良いです。)
証明の例を書いておきます。
(証明)
\(\,\mathrm{△ESR}\,\)と\(\,\mathrm{△FDR}\,\)において
\(\,\mathrm{EF}\,\)は線分\(\,\mathrm{AP}\,\)の垂直二等分線
\(\,\mathrm{GH}\,\)は線分\(\,\mathrm{DP}\,\)の垂直二等分線
であることから
\(\,\mathrm{R}\,\)は\(\,\mathrm{△ADP}\,\)と\(\,\mathrm{△ASD}\,\)の外接円の中心で、
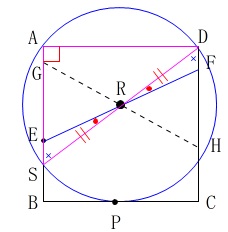
\(\,\mathrm{\color{magenta}{SR}=\color{magenta}{DR}}\,\) ・・・①
また正方形\(\,\mathrm{ABCD}\,\)の対辺は平行で、
平行線の錯角は等しいので
\(\mathrm{\color{blue}{∠RSE}=\color{blue}{∠RDF}}\) ・・・②
対頂角は等しいので
\(\mathrm{\color{red}{∠ERS}=\color{red}{∠FRD}}\) ・・・③
①②③より
\(\,1\,\)組の辺とその両端の角がそれぞれ等しい
ので
\(\,\mathrm{△ESR}\,\) ≡ \(\,\mathrm{△FDR}\,\)
(終わり)
(2)で利用した中心の作図は単なる作図問題ではなく、
(3)の誘導になっていたということですね。
分かってしまえば簡単ですが、合同の証明でここまで結論が遠いとなかなか気がつかなかったのではないでしょうか。
(1)(2)の折り返しで何が等しいかを図にしっかり書き込んでいるかどうかがポイントですね。
2018年度の滋賀県公立入試の数学問題はここまでです。
⇒ 滋賀県公立高校入試問題2018(平成30年度)数学の解説
前半は基本的な計算や公式利用の問題でした。
後半は基本からその基本の組み合わせとなる応用になっているのでかなり差がつく問題と言えます。
一つひとつの問題をその場しのぎの答えをだすということで終わらせてしまうと、
後の問題につながらないようになっていますので、
各問ごとに全体を通じて何が言えるかをおさえておく練習をしておいた方が良いですね。
\(\,2019\,\)年以降の滋賀県の数学問題も解説を追加更新しますので見ておくと良いですよ。
