滋賀県で行われた公立高校入試2019年(平成31年)度の数学問題の解説です。
小問集合の計算問題から、グラフや図の読み取りをしっかりやらないと答えまでたどり着かない応用問題が並びます。
ポイントは読み取った条件から次の条件につなげるように手を動かすことです。
問題は滋賀県が公開してくれています。
1.小問集合
\(\color{black}{\fbox{ 1 }}\)は正負の数、式の計算、方程式、関数、確率、図形の基本性質から作図までの基本問題が\(\,12\,\)問あります。
小問集合ですが基本的な計算問題と標準から応用と言える問題がありますので、
目標点数に合わせて全問を見渡してあまり時間をかけずにすませておくと良いでしょう。
正負の数の性質と文字式の計算
(1)
正の数と負の数の基本です。
最高気温と最低気温の差が\(\,\color{blue}{19}\,\)℃で、
最高気温が\(\,\color{red}{15}\,\)℃です。
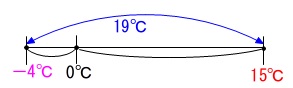 最低気温は、最高気温から\(\,\color{blue}{19}\,\)℃低い温度となります。
最低気温は、最高気温から\(\,\color{blue}{19}\,\)℃低い温度となります。
\(\hspace{10pt}\color{red}{15}-\color{blue}{19}\\
=\underline{ -4 } ℃\)
数直線上で見ればすぐに分かりますね。
差を上下で見たい人は自分で縦に気温を書いて比べて下さい。
(2)
文字式の計算です。
\(\hspace{10pt}\displaystyle \frac{1}{4}a-\frac{5}{6}a+a\\
\displaystyle =\frac{3a-10a+12a}{12}\\
\displaystyle =\underline{ \frac{5a}{12} }\)
分数計算では分母を1つにすると分子の計算に集中できるのでミスが減ります。
『覚え太郎』会員は当たり前にやっていると思いますけど。笑
答え\(\,\displaystyle \frac{5\color{red}{a}}{12}\,\)の分子の\(\,\color{red}{a}\,\)は横に書いても問題ありません。
答え \(\displaystyle \underline{ \frac{5}{12}\,a }\)
ただし、分数係数の横にある文字\(\,a\,\)が分子にあることは忘れないようにしましょう。
方程式と無理数の計算
(3)
連立方程式を解くだけです。
移項して代入法でも良いですが加減法で簡単に終わらせましょう。
\( \begin{cases}
\hspace{7pt} x-2y=7 ・・・①\\ \\
\hspace{7pt} 4x+3y=6 ・・・②
\end{cases}\)
連立方程式を解くときの基本は一文字消去です。
\(\,y\,\)を消しても良いですが、\(\,y\,\)を消去するには方程式を両方変形しなければならないので\(\,x\,\)を消します。
どちらでも良いですよ。
\(\,①\times 4-②\,\)から
\(\hspace{12pt}4x-8y=28\\
\underline{-)\,4x+3y=6}\\
\hspace{19pt}-11y=22\\
\hspace{40pt}y=-2\)
この\(\,y=-2\,\)を①に代入して
\(\begin{eqnarray}
x-2(-2)&=&7\\
x+4&=&7\\
x&=&7-4\\
&=&3
\end{eqnarray}\)
代入するときは正の数負の数関係なく(かっこ)をつけておくとミスが減ります。
答え \(\,\underline{ x=3\,,\,y=-2 }\,\)
(4)
無理数の分母の有理化と足し算です。
\(\hspace{10pt}\displaystyle \sqrt{27}+\frac{12}{\sqrt{3}}\\
\displaystyle =3\sqrt{3}+\frac{12\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}\\
\displaystyle =3\sqrt{3}+\frac{12\sqrt{3}}{3}\\
=3\sqrt{3}+4\sqrt{3}\\
=\underline{ 7\sqrt{3} }\)
ルートの中が同じ場合だけルートの前の整数部分の足し算引き算ができます。
暗算でできる計算ですが、素因数分解、有理化ともに慎重にやった方が良いですよ。
計算ミス1つで\(\,4\,\)点マイナスです。
(5)
\(\,2\,\)次方程式を解くときは因数分解から試すと良いですね。
方程式では左辺にすべての項を集めて、右辺を\(\,0\,\)にしてから解くのが基本です。
\(\begin{eqnarray}
\color{red}{2x^2+4x-7}&=&\color{blue}{x^2-2}\\
\color{red}{2x^2+4x-7}\color{blue}{-x^2+2}&=&0\\
x^2+4x-5&=&0\\
(x-1)(x+5)&=&0\\
x&=&\underline{ 1\,,\,-5 }
\end{eqnarray}\)
因数分解できないとき解の公式利用です。
(6)
文字式の計算です。
割り算は逆数のかけ算としてあつかうのがはやいです。
\(\hspace{10pt}14x^2y\color{red}{\div (-7y)^2}\times 28xy\\
\displaystyle =\frac{14x^2y\times 28xy}{\color{red}{(-7y)^2}}\\
\displaystyle =\frac{14x^2y\times 28xy}{49y^2}\\
=\underline{ 8x^3 }\)
割り算の直後の文字式を分母に回します。
分数線を1つしか書いていませんが、分けて書いても良いですよ。
\(\hspace{10pt}14x^2y\div (-7y)^2\times 28xy\\
\displaystyle =14x^2y\times \frac{1}{(-7y)^2}\times 28xy\\
\displaystyle =14x^2y\times \frac{1}{49y^2}\times 28xy\\
=\underline{ 8x^3 }\)
ただし、この場合は分母と分子をはっきりと分けるために、
\(\hspace{10pt}14x^2y\div (-7y)^2\times 28xy\\
\displaystyle =\frac{14x^2y}{1}\times \frac{1}{(-7y)^2}\times \frac{28xy}{1}\\
\displaystyle =\frac{14x^2y}{1}\times \frac{1}{49y^2}\times \frac{28xy}{1}\\
=\underline{ 8x^3 }\)
分母を\(\,1\,\)として分母と分子をはっきり分けた方がわかりやすいです。
関数の座標と確率
(7)
放物線の座標を求めます。
関数\(\,y=-7x^2\,\)と\(\,y\,\)座標が\(\,-28\,\)と分かっているので代入するだけです。
\(\begin{eqnarray}
-28&=&-7x^2\\
4&=&x^2\\
x&=&\underline{ \pm 2 }
\end{eqnarray}\)
 同じ\(\,y\,\)の値に対し、\(\,x\,\)は2つあるので注意しましょう。
同じ\(\,y\,\)の値に対し、\(\,x\,\)は2つあるので注意しましょう。
(8)
確率です。
樹形図で良いですが、色によって玉の数が違うので玉を一つひとつ区別します。
白玉は文字の色を白にすると見えないので黒数字のままにしておきます。
青玉\(\,3\,\)個を\(\,\color{blue}{1},\color{blue}{2},\color{blue}{3}\,\)
白玉\(\,2\,\)個を\(\,4,5\,\)
赤玉\(\,1\,\)個を\(\,\color{red}{6}\,\)
として考えます。
取り出した玉は袋にもどして二回目をとるので同じ玉を取り出すこともあります。
\(\begin{array}{|c|c|c|c|c|} \hline
\color{blue}{1} & \color{blue}{1} & \color{blue}{●} & 4 & \color{blue}{1} & \color{red}{●}\\ \hline
\color{blue}{1} & \color{blue}{2} & \color{blue}{●} & 4 & \color{blue}{2} & \color{red}{●}\\ \hline
\color{blue}{1} & \color{blue}{3} & \color{blue}{●} & 4 & \color{blue}{3} & \color{red}{●}\\ \hline
\color{blue}{1} & 4 & \color{red}{●}& 4 & 4 &\\ \hline
\color{blue}{1} & 5 & \color{red}{●}& 4 & 5 & \\ \hline
\color{blue}{1} & \color{red}{6} & & 4 & \color{red}{6} &\\ \hline
\color{blue}{2} & \color{blue}{1} & \color{blue}{●} & 5 & \color{blue}{1} & \color{red}{●}\\ \hline
\color{blue}{2} & \color{blue}{2} & \color{blue}{●} & 5 & \color{blue}{2} & \color{red}{●}\\ \hline
\color{blue}{2} & \color{blue}{3} & \color{blue}{●} & 5 & \color{blue}{3} & \color{red}{●}\\ \hline
\color{blue}{2} & 4 & \color{red}{●}& 5 & 4 &\\ \hline
\color{blue}{2} & 5 & \color{red}{●}& 5 & 5 & \\ \hline
\color{blue}{2} & \color{red}{6} & & 5 & \color{red}{6} &\\ \hline
\color{blue}{3} & \color{blue}{1} & \color{blue}{●} & \color{red}{6} & \color{blue}{1} &\\ \hline
\color{blue}{3} & \color{blue}{2} & \color{blue}{●} & \color{red}{6} & \color{blue}{2} &\\ \hline
\color{blue}{3} & \color{blue}{3} & \color{blue}{●} & \color{red}{6} & \color{blue}{3} & \\ \hline
\color{blue}{3} & 4 & \color{red}{●}& \color{red}{6} & 4 &\\ \hline
\color{blue}{3} & 5 & \color{red}{●}& \color{red}{6} & 5 & \\ \hline
\color{blue}{3} & \color{red}{6} & & \color{red}{6} & \color{red}{6} &\\ \hline
\end{array}\)
青玉が\(\,2\,\)回出る確率は
\(\displaystyle \frac{9}{36}=\underline{ \frac{1}{4} } \) \(\color{black}{ \fbox{(a)} }\)
青玉と白玉が\(\,1\,\)回ずつ出る確率は、
青→白 または 白→青の場合があるので
\(\displaystyle \frac{12}{36}=\underline{ \frac{1}{3} } \) \(\color{black}{\fbox{ (b) }}\)
したがって、青玉と白玉が1回ずつ出る場合の方が起こりやすい。
答え \(\,\underline{ イ } \,\) \(\color{black}{\fbox{ (c) }}\)
\(\displaystyle \frac{1}{4}=\frac{3}{12}\)
\(\displaystyle \frac{1}{3}=\frac{4}{12}\)
分母をそろえると分子の大きさで大小比較が簡単にできます。
相似を利用した線分の長さと作図
(9)
相似を利用した線分の長さと作図です。
作図は三平方の定理(三角定規の比)を逆に利用した方法です。
\(\,\mathrm{△ABC}\,\)は二等辺三角形なので、\(\,2\,\)辺が等しいことと同時に底角が等しくなることは最初に図に書き込んでおくと良いですよ。
①
\(\,\mathrm{BD}\,\)の長さを求めます。
条件
\(\,\mathrm{AB=9}\,\)
\(\,\mathrm{BC=6}\,\)
\(\,\mathrm{BE=3}\,\)
\(\,\mathrm{∠BAC=∠BDE}\,\)
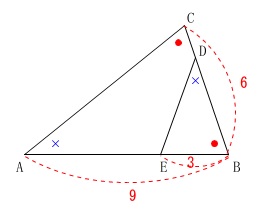 \(\,2\,\)組の角がそれぞれ等しいので相似が言えますが、
\(\,2\,\)組の角がそれぞれ等しいので相似が言えますが、
相似を証明する必要はありません。
\(\,\mathrm{△ABC}\,\) ∽ \(\,\mathrm{△DEB}\,\)
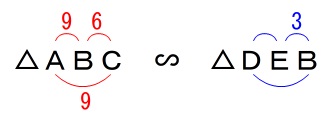 比例式を立てればすぐに答えです。
比例式を立てればすぐに答えです。
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{BC}:\color{blue}{EB}}&=&\mathrm{\color{red}{AC}:\color{blue}{DB}}\\
\color{red}{6}:\color{blue}{3}&=&\color{red}{9}:\mathrm{\color{blue}{DB}}\\
6\times \mathrm{DB}&=&3\times 9\\
\displaystyle \mathrm{DB}&=&\frac{3\times 9}{6}\\
\displaystyle &=&\underline{ \frac{9}{2} }
\end{eqnarray}\)
②
\(\,\mathrm{BC}\,\) ∥ \(\,\mathrm{FG}\,\) となるように、
\(\,\mathrm{△AFG}\,\)の面積が\(\,\mathrm{△ABC}\,\)の面積の半分になる、
\(\,2\,\)点\(\,\mathrm{E,F}\,\)を\(\,\mathrm{AB,AC}\,\)上に作図します。
\(\,\mathrm{BC}\,\) ∥ \(\,\mathrm{FG}\,\)のとき
\(\,\mathrm{△ABF}\,\)と\(\,\mathrm{△ABC}\,\)は相似になるので、
面積比が\(\,\color{red}{1}:\color{blue}{2}\,\)
なので
線分比は\(\,\color{red}{1}:\color{blue}{\sqrt{2}}\,\)
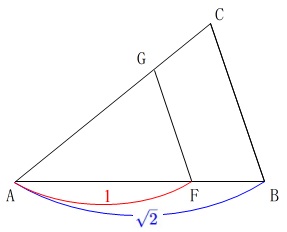
となれば良いということですが、直角二等辺三角形の三角定規の辺の比を利用します。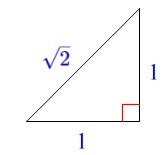
といってもすぐには思いつかないかもしれませんが、\(\,\mathrm{AB}\,\)を直径とする円を利用します。
中心が知りたいので\(\,\mathrm{AB}\,\)の垂直二等分線を引いて、
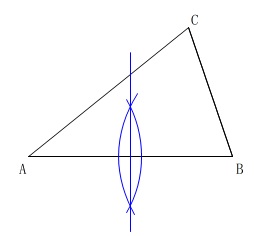 \(\,\mathrm{AB}\,\)との交点を中心とする円を書き、
\(\,\mathrm{AB}\,\)との交点を中心とする円を書き、
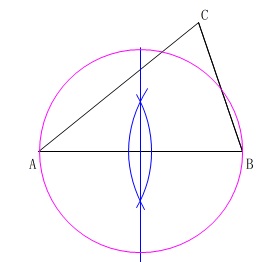
円と垂直二等分線との交点の交点を頂点とする直角二等辺三角形で辺の比を利用します。
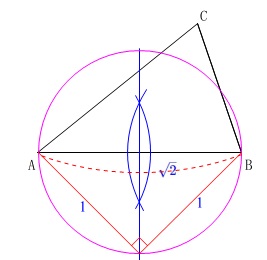 ポイントはここですが、
ポイントはここですが、
そのときに\(\,\mathrm{A}\,\)を中心とする円を書けば、
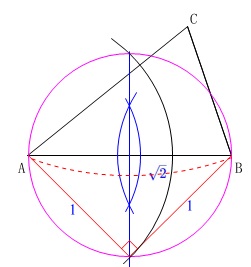
辺の比が\(\,1:\sqrt{2}\,\)となる線分比になり、
\(\,\mathrm{△AFG}\,\)の面積が\(\,\mathrm{△ABC}\,\)の半分になります。
理由を書く必要はないので、作図としては
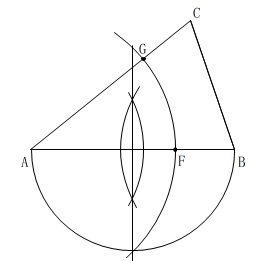 問題は斜め向いているだけです。
問題は斜め向いているだけです。
説明すると長くてややこしそうに見えますが、
面積比が\(\,1:2\,\)なら相似比が\(\,1:\sqrt{2}\,\)で、
直角二等辺三角形の辺の比を利用して円を書く、それだけです。
\(\color{black}{\fbox{ 1 }}\)は問題数が多いのでここで区切ります。
⇒ 滋賀県公立高校入試2019年数学第2問データの活用問題の解説
\(\color{black}{\fbox{ 2 }}\)はデータの活用です。
(更新頻度が落ちていますが時間があるとき更新します、)
⇒ 2019年(平成31年)度滋賀県公立高校入試の数学第3問の解説
\(\color{black}{\fbox{ 3 }}\)は一度に解決しようとすると難しく感じますが、一つひとつ見ていけばわかりやすいです。
⇒ 2019年(平成31年)度滋賀県公立高校入試の数学第4問の解説
\(\color{black}{\fbox{ 4 }}\)は正多角形の問題です。
対称性を見抜けば計算も楽に終わります。
更新はこちらで確認できます。
