2019年愛知県公立高校入試A日程の数学問題と解説【第3問】

2019年(平成31年度)に愛知県で行われた公立高校入試、全日制課程Aの数学問題と第3問の解説です。
第3問は平面図形の問題ですがすぐに公式で答えが出るという基本問題ではなく、少し応用された問題なので少し時間を要します。
この第3問で差がつきやすいですが、逆に差をつける側にまわれば良いだけですよ。

問題は愛知県が公表してくれています。

⇒　2019年度A日程数学問題

　\(\,\large{3}\,\)

(1)(2)(3)とありますがつながりはありませんので、別問題として一つ一つ解いていけば良いですよ。

弧の長さと中心角

(1)
角度を求める問題です。
手がかりとなるのは円の半径と弧の長さだけです。

　円の半径\(\,5\,\)
　弧の長さ\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{ＣＤ}}=2\,\pi}\,\)

弧の長さと中心角は比例するので比例式を利用します。

半径\(\,5\,\)の円周は\(\,10\,\pi\,\)なので、
\(\,2\,\pi\,\)に対する中心角\(\,\mathrm{∠COD}\,\)との関係は

　\(\,\mathrm{10\,\pi:2\,\pi=360^{\circ}:∠COD}\,\)

よって、

　\(\,\mathrm{∠COD=72^{\circ}}\,\)
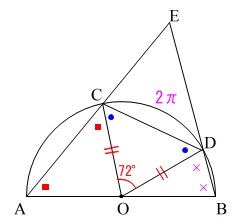さらに、半径は常に等しいから\(\,\mathrm{△COD}\,\)は二等辺三角形なので、

　\(\begin{eqnarray}\displaystyle
\mathrm{∠ODC}&=&\mathrm{∠OCD}\\
&=&\frac{180-72}{2}\\
&=&54　(度)
\end{eqnarray}\)

実はこの角度は\(\,\mathrm{∠AEB}\,\)（\(\,\mathrm{∠CED}\,\)）と同じになるのですが簡単に説明しておきます。
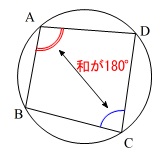内接する四角形の対角の和は\(\,180°\,\)になります。

これが分からない人は『覚え太郎』からやり直しておくと良いですよ。

⇒　中学数学を短期攻略する『覚え太郎』

よく見かける事実なので詳しい説明は省略します。

このとき内接する四角形の1つの外角は対角に等しくなります。
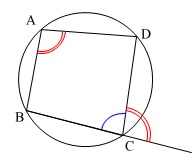このことから、図の角度を\(\,\color{red}{a},\color{magenta}{b},x\,\)を用いて表すと、
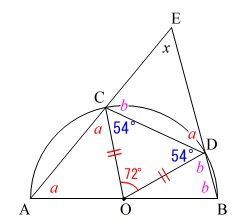角度の関係式は、直線の表す角度から

　\(\color{red}{a}+\color{blue}{54^{\circ}}+\color{magenta}{b}=180^{\circ}　･･･①\)

また、\(\,\mathrm{△ABE}\,\)の内角の和も\(\,180°\,\)なので

　\(\color{red}{a}+x+\color{magenta}{b}=180^{\circ}　･･･②\)

①②を見比べるだけで

　\(x=\color{blue}{54^{\circ}}\)

は分かると思いますが一応計算しておきます。

①から

　\(\begin{eqnarray}
\color{red}{a}+\color{magenta}{b}&=&180^{\circ}-54^{\circ}\\
&=&126^{\circ}
\end{eqnarray}\)

②から

　\(\begin{eqnarray}
x+\color{red}{a}+\color{magenta}{b}&=&180^{\circ}\\
x&=&180^{\circ}-(\color{red}{a}+\color{magenta}{b})\\
&=&180^{\circ}-126^{\circ}\\
&=&\underline{　54^{\circ}　}
\end{eqnarray}\)

説明ほど時間のかかる問題ではありません。

次に行きましょう。

六角形の辺の長さと面積

(2)
ややこしそうな六角形がありますが、内角がすべて同じなので、
少し計算量は増えますが長さや面積は簡単に出ます。

条件を書き出しておきます。

　六角形\(\,\mathrm{ABCDEF}\,\)の内角はすべて等しい。
　\(\,\mathrm{AB=AF=4}\,\)
　\(\,\mathrm{ED=3}\,\)
　\(\,\mathrm{FE=2}\,\)
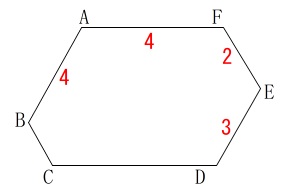（見やすくするために、長さは合わせていません。）

六角形の内角はすべて\(\,\color{red}{120°}\,\)です。
内角がすべて等しいということは、外角もすべて等しくなります。

外角の和は常に\(\,360°\,\)なので、

　\(\begin{eqnarray}
　(1つの外角)&=&\frac{360^{\circ}}{6}\\
&=&60^{\circ}
\end{eqnarray}\)

よって内角はすべて\(\,120°\,\)になります。

あれこれ考えるより三角定規を利用しましょう。
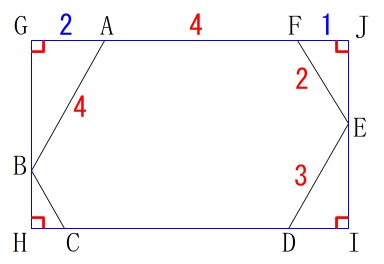四すみの直角三角形はすべて三角定規です。

それぞれの長さは、

　\(\mathrm{AG}=\color{blue}{2}\,,\,\displaystyle \mathrm{GB}=\color{magenta}{2\sqrt{3}}\,\)
　\(\mathrm{FJ}=\color{blue}{1}\,,\,\mathrm{JE}=\color{magenta}{\sqrt{3}}\)
　\(\displaystyle \mathrm{DI}=\color{blue}{\frac{3}{2}}\,,\,\displaystyle \mathrm{EI}=\color{magenta}{\frac{3\sqrt{3}}{2}}\)
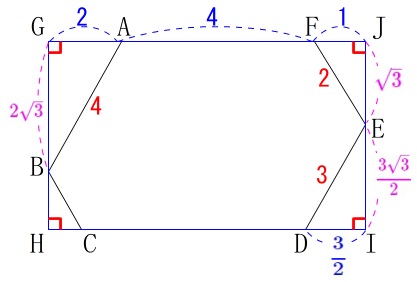\(\,\mathrm{GH=JI}\,\)から

　\(\begin{eqnarray}\displaystyle
\mathrm{GB+BH}&=&\mathrm{JE+EI}\\
\color{magenta}{2\sqrt{3}}+\mathrm{BH}&=&\color{magenta}{\sqrt{3}}+\color{magenta}{\frac{3\sqrt{3}}{2}}\\
\mathrm{BH}&=&\color{magenta}{\frac{\sqrt{3}}{2}}
\end{eqnarray}\)

このとき、\(\,\mathrm{BH:CH=\sqrt{3}:1}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{BH}:\mathrm{CH}&=&\sqrt{3}:1\\
\frac{\sqrt{3}}{2}:\mathrm{CH}&=&\sqrt{3}:1\\
\sqrt{3}\times\,\mathrm{CH}&=&\frac{\sqrt{3}}{2}\\
&=&\color{blue}{\frac{1}{2}}
\end{eqnarray}\)
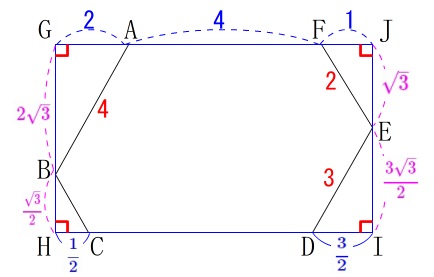今度は\(\,\mathrm{GJ=HI}\,\)から

　\(\begin{eqnarray}\displaystyle
\mathrm{GA+AF+FJ}&=&\mathrm{HC+\color{red}{ＣＤ}+DI}\\
\color{blue}{2}+\color{blue}{4}+\color{blue}{1}&=&\color{blue}{\frac{1}{2}}+\mathrm{\color{red}{ＣＤ}}+\color{blue}{\frac{3}{2}}\\
\mathrm{\color{red}{ＣＤ}}&=&\underline{　5　}
\end{eqnarray}\)

面積はいろいろな計算方法が考えられますが、
長方形から四隅の直角三角形を引けば良いでしょう。

　\(\begin{eqnarray}\displaystyle
\mathrm{JI}&=&\mathrm{JE+EI}\\
&=&\sqrt{3}+\frac{3\sqrt{3}}{2}\\
&=&\color{red}{\frac{5\sqrt{3}}{2}}
\end{eqnarray}\)
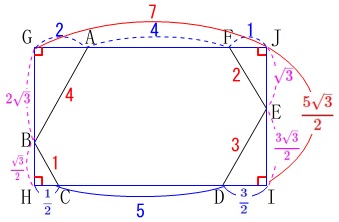長方形\(\,\mathrm{GHIJ}\,\)の面積\(\,\mathrm{\color{red}{S}}\,\)は

　\(\begin{eqnarray}
\color{red}{\mathrm{S}}&=&\mathrm{GJ}\times \mathrm{JI}\\
&=&7\times \frac{5\sqrt{3}}{2}\\
&=&\color{red}{\frac{35\sqrt{3}}{2}}
\end{eqnarray}\)

これから4つの直角三角形の面積を引いても良いです。
ここでは相似比を利用して計算しておきます。
左下の\(\,\mathrm{\color{red}{△BCH}}\,\)の面積は

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{△BCH}}&=&\frac{1}{2}\times \mathrm{CH}\times \mathrm{BH}\\
&=&\frac{1}{2}\times \color{blue}{\frac{1}{2}}\times \color{magenta}{\frac{\sqrt{3}}{2}}\\
&=&\color{red}{\frac{\sqrt{3}}{8}}
\end{eqnarray}\)
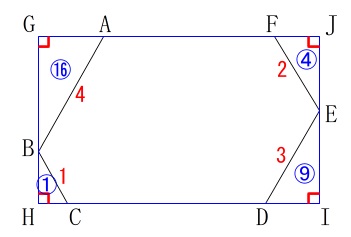ここで4つの直角三角形は、
　
　相似比　\(\,\color{red}{1}:\color{red}{2}:\color{red}{3}:\color{red}{4}\,\)

なので

　面積比　\(\color{blue}{1}:\color{blue}{4}:\color{blue}{9}:\color{blue}{16}\)

面積比1に相当する\(\,\mathrm{△BCH}\,\)の面積は求めてあるので、
直角三角形4つ分の面積の和\(\,\mathrm{\color{blue}{T}}\,\)は、

　\(\begin{eqnarray}
\mathrm{\color{blue}{T}}&=&\color{red}{\frac{\sqrt{3}}{8}}\times (1+4+9+16)\\
&=&\frac{\sqrt{3}}{8}\times 30\\
&=&\color{blue}{\frac{15\sqrt{3}}{4}}
\end{eqnarray}\)

よって求める六角形の面積は、長方形から4つの直角三角形を引けば良いので、

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{S}}-\mathrm{\color{blue}{T}}&=&\color{red}{\frac{35\sqrt{3}}{2}}-\color{blue}{\frac{15\sqrt{3}}{4}}\\
&=&\frac{70\sqrt{3}-15\sqrt{3}}{4}\\
&=&\underline{　\frac{55\sqrt{3}}{4}　}　(\mathrm{cm^2})
\end{eqnarray}\)

他にも、\(\,\mathrm{BC}\,\)と\(\,\mathrm{FE}\,\)などが平行
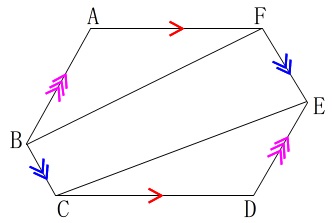になることなどを利用しても求まりますが後があるので省略します。
長さを三角定規の比から出せれば、
台形\(\,\mathrm{BCEF}\,\)の高さ\(\,\mathrm{BF}\,\)は三平方の定理から分かるので、
三角形2つ\(\,\mathrm{△ABF}\,\)と\(\,\mathrm{△CDE}\,\)の面積を加えてみて下さい。

円の面積と回転体の体積比較

(3)
円と接線の位置関係をしっかり理解していれば、

　円の面積　\(\pi\,r^2\)
　球の体積　\(\displaystyle \frac{4}{3}\,r^3\)
　円錐の体積　\(\displaystyle \frac{1}{3}\,\pi\,r^2\,h\)

を利用するだけです。

相似に関する問題が少ないな、と思いながら解いているとここにありました。

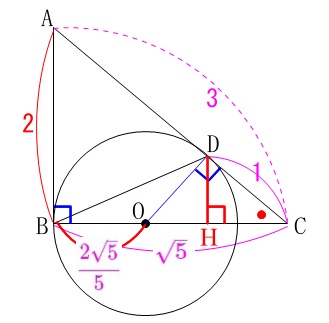
条件です。

　\(\,\mathrm{AB,AC}\,\)は円\(\,\mathrm{O}\,\)の接線
　\(\,\mathrm{AB=2}\,\)
　\(\,\mathrm{AC=2}\,\)
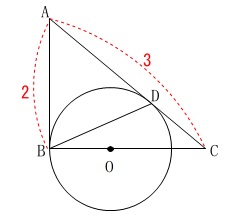円の外にある\(\,1\,\)点から\(\,2\,\)本の接線を引くと、

　接点までの距離は等しくなり、半径とは垂直になる

ことが分かります。

さらに、\(\,\mathrm{AD,AC}\,\)の長さは分かっているので

　\(\begin{eqnarray}
\mathrm{AC}&=&\mathrm{AD+DC}\\
\color{red}{3}&=&\color{blue}{2}+\mathrm{DC}\\
\mathrm{DC}&=&\color{magenta}{1}
\end{eqnarray}\)

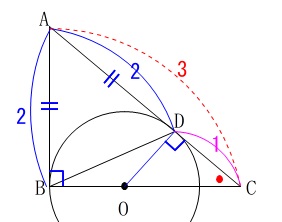
①
円\(\,\mathrm{O}\,\)の面積を求めますが、相似な三角形から半径が求まります。

　\(\,\mathrm{∠BCA}\,\)は共通の角で、
　\(\,\mathrm{∠ABC=∠ODC=90^{\circ}}\,\)

　\(\,2\,\)組の角がそれぞれ等しいので

　\(\,\mathrm{△CBA}\,\)　∽　\(\,\mathrm{△CDO}\,\)

三平方の定理から

　\(\begin{eqnarray}
\mathrm{AB^2+BC^2}&=&\mathrm{AC^2}\\
2^2+\mathrm{BC^2}&=&3^2\\
\mathrm{BC^2}&=&9-4\\
&=&5\\
\mathrm{BC}&=&\color{magenta}{\sqrt{5}}　(\mathrm{BC}＞0)
\end{eqnarray}\)
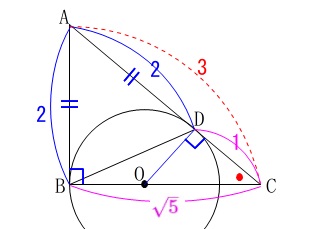よって円\(\,\mathrm{O}\,\)の半径\(\,\mathrm{OD}\,\)は相似比から求めることができます。

　\(\begin{eqnarray}\displaystyle
\mathrm{AB:OD}&=&\mathrm{BC:DC}\\
\color{blue}{2}:x&=&\color{magenta}{\sqrt{5}}:\color{magenta}{1}\\
\sqrt{5}x&=&2\\
x&=&\frac{2}{\sqrt{5}}
\end{eqnarray}\)

円\(\,\mathrm{O}\,\)の半径がでました。

有理化しても良いですが円の面積を求めるときに\(\,2\,\)乗するのでそのままにしておきます。

②で球の体積を求めるときに必要になるので、
無理数の処理に慣れていない場合は有理化しておきましょう。

　\(\displaystyle \frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}\)

求める円\(\,\mathrm{\mathrm{O}}\,\)の面積\(\,\mathrm{\mathrm{S}}\,\)は、

　\(\begin{eqnarray}\displaystyle
\mathrm{S}&=&\pi\,\left(\frac{2}{\sqrt{5}}\right)^2\\
&=&\underline{　\frac{4}{5}\,\pi　}　(\mathrm{cm^2})
\end{eqnarray}\)

②
回転体の体積比較です。

1つは円錐2つ分、もう1つは円を直径を軸に回転させるので球です。

どちらも軸は\(\,\mathrm{BC}\,\)です。
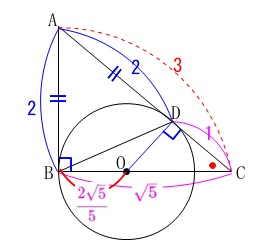長さは①で求めているのでそのまま利用します。

回転体の見取り図を簡単に考えておきましょう。

\(\,\mathrm{△DBC}\,\)を\(\,\mathrm{BC}\,\)を軸として回転させると円錐2つ分になります。

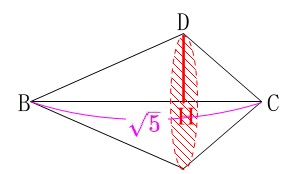このときの底面の半径\(\,\mathrm{DH}\,\)は、
　\(\,\mathrm{△CDH}\,\)　∽　\(\,\mathrm{△CAB}\,\)

で相似比が　\(\mathrm{CD:CD}=1:3\)　なので、

　\(\begin{eqnarray}
\mathrm{\color{red}{DH}}&=&\frac{1}{3}\times \mathrm{AB}\\
&=&\frac{1}{3}\times 2\\
&=&\color{red}{\frac{2}{3}}
\end{eqnarray}\)

よって\(\,\mathrm{△DBC}\,\)の回転体の体積\(\,\mathrm{V_1}\,\)は

　\(\begin{eqnarray}\displaystyle
\mathrm{V_1}&=&\frac{1}{3}\times \pi\,\left(\color{red}{\frac{2}{3}}\right)^2\times \color{magenta}{\sqrt{5}}\\
\end{eqnarray}\)

球の体積との比較なので後で割り算することになるので、この計算はしなくて良いですが一応やっておきます。

　\(\begin{eqnarray}\displaystyle
\mathrm{V_1}&=&\frac{1}{3}\times \pi\,\left(\color{red}{\frac{2}{3}}\right)^2\times \color{magenta}{\sqrt{5}}\\
&=&\frac{4\sqrt{5}}{27}\,\pi
\end{eqnarray}\)

2つの円錐を1つの円錐として計算していますが、説明しておきます。
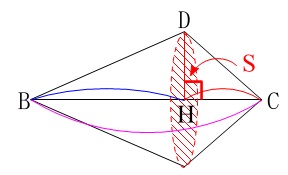　\(\,\mathrm{△DBC}\,\)の回転体の体積は、

底面積\(\,\mathrm{S}\,\)で、高さが\(\,\mathrm{\color{blue}{BH}}\,\)と\(\,\mathrm{\color{red}{CH}}\,\)の2つの円錐の合わさった立体で、

　\(\begin{eqnarray}
\mathrm{V_1}&=&\frac{1}{3}\times \mathrm{S}\times \,\mathrm{\color{blue}{BH}}+\frac{1}{3}\times \mathrm{S}\times \mathrm{\color{red}{HC}}\\
&=&\frac{1}{3}\times \mathrm{S}\times (\,\underline{\mathrm{\color{blue}{BH}+\color{red}{HC}}}\,)\\
&=&\frac{1}{3}\times \mathrm{S}\times \underline{\mathrm{\color{magenta}{BC}}}
\end{eqnarray}\)

となるので1つの円錐として計算しても同じなのです。

次に球の体積です。

　半径は\(\displaystyle \color{magenta}{\frac{2\sqrt{5}}{5}}\)

なので円\(\,\mathrm{O}\,\)の回転体である球の体積\(\,\mathrm{V_2}\,\)は

　\(\begin{eqnarray}\displaystyle
\mathrm{V_2}&=&\frac{4}{3}\times \,\pi\,\times\left(\frac{2\sqrt{5}}{5}\right)^3\\
&=&\frac{4}{3}\times \,\pi\,\times\left(\frac{8\times 5\sqrt{5}}{125}\right)\\
&=&\frac{32\sqrt{5}}{75}\,\pi
\end{eqnarray}\)

よって、\(\,\mathrm{V_1}\,\)は\(\,\mathrm{V_2}\,\)の

　\(\begin{eqnarray}\displaystyle
\mathrm{\frac{V_1}{V_2}}&=&\frac{4\sqrt{5}}{27}\,\pi\div \frac{32\sqrt{5}}{75}\,\pi\\
&=&\frac{4\sqrt{5}}{27}\,\pi\times \frac{75}{32\sqrt{5}\,\pi}\\
&=&\frac{1}{9}\times \frac{25}{8}\\
&=&\underline{　\frac{25}{72}　}　(倍)
\end{eqnarray}\)

　（問題はこれで終わりです。）　←　問題用紙に書いてあります。

解説は以上です。

もっと詳しくしても良いのですが長くなるのでやめておきます。
いろいろな知識を問われているので良い復習になる問題です。

じっくり取り組んでおくと良いですね。

⇒　愛知県公立高校入試2019年A日程の数学問題と解説

　\(\,\large{1}\,\)　は計算主体の小問集合です。

⇒　愛知県公立高校入試2019年A日程の数学問題と解説【第2問】

　\(\,\large{2}\,\)　は文字式や確率の小問集合です。

⇒　愛知県の公立高校入試数学過去問の問題と解答解説

\(\,2020\,\)年の問題解説やB日程問題の解説もしてあります。