愛知県公立高校入試2019年A日程の数学問題と解説【第2問】

2019年(平成31年度)に愛知県で行われた公立高校入試、全日制課程Aの数学問題と第2問の解説です。
第2問は規則性と文字式、合同な図形、確率、関数とグラフの読み取り問題の集合です。
それほどややこしい計算があるわけではありませんので、第3問に時間を残せるように手際よく処理したい所です。

問題は愛知県が公表してくれています。

⇒　2019年度A日程数学問題

　\(\,\large{2}\,\)

(1)
奇数の並びと、その積が書かれた規則性の読み取り問題です。
文字式を使って方程式を立てればすぐに終わります。

　\(\,1\,\)段目は奇数の並び
　\(\,2\,\)段目は一つの奇数とその次の奇数の積

が並んでいます。

\(\color{black}{\fbox{　ア　}}\)と\(\color{black}{\fbox{　イ　}}\)は連続する2つの奇数なので、

　ア：\(\,\color{red}{2n-1}\,\)
　イ：\(\,\color{blue}{2n+1}\,\)

と整数\(\,n\,\)を用いて文字式で表すと、
その積　\(\,(\color{red}{2n-1})(\color{blue}{2n+1})\,\)　が\(\,899\,\)だから

　\(\begin{eqnarray}
(\color{red}{2n-1})(\color{blue}{2n+1})&=&899\\
4n^2-1&=&899\\
4n^2&=&900\\
n^2&=&225\\
\end{eqnarray}\)

自然数の並びだから\(\,n\,\)は正の整数として問題ないので、

　\(n=15\)

このとき、

　\(\hspace{10pt}\color{red}{2n-1}\\
=2\times 15-1\\
=\underline{　29　}　\color{black}{\fbox{ア}}\)

　\(\hspace{10pt}\color{blue}{2n+1}\\
=2\times 15+1\\
=\underline{　30　}　\color{blue}{\fbox{イ}}\)

\(\,225\,\)は素因数分解すると

　\(225=3^2\times 5^2\)

です。（素因数分解は自分でやりましょう。）
『覚え太郎』会員は基礎編で\(\,16\,\)の平方数まで覚えているので素因数分解するまでもありませんね。

それと、\(\color{black}{\fbox{ア}}\)と\(\color{black}{\fbox{イ}}\)ですが、

　ア：\(\,a\,\)
　イ：\(\,a+2\,\)

とおいても結果は同じですが、因数分解するとき

　\(\begin{eqnarray}
a(a+2)&=&899\\
a^2+2a-899&=&0\\
(a-29)(a+31)&=&0
\end{eqnarray}\)

と、定数項が素数の大きな積になります。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

\(\,2\,\)連続奇数の表し方は覚えておいた方が何かと楽ですよ。

⇒　数学の問題と会話できるようになる『覚え太郎』

自分で言うのもなんですが、オススメです。笑

(2)
正方形が2つ重なる、これも良くある問題です。

『覚え太郎』会員は「平行と合同」のカード【合同発見シリーズ】を見直しておいて下さい。

条件を図に書き込んで等しい角度を示します。
長さは具体的には必要無いので、辺については等しいことだけ分かるようにすれば良いだけですよ。
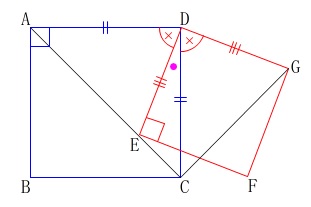共通になっている\(\,\mathrm{\color{magenta}{∠EDC}}\,\)があることに気がつけば合同の証明は簡単です。

先ずは合同の証明をします。

　\(\,\mathrm{△AED}\,\)と\(\,\mathrm{△CGDF}\,\)で
正方形の\(\,1\,\)辺になっているので
　\(\,\mathrm{ＡＤ=ＣＤ}\,\)　･･･①
　\(\,\mathrm{ＥＤ=ＧＤ}\,\)　･･･②
正方形の4つの角は皆等しく\(\,90°\,\)で、
共通の\(\,\mathrm{\color{magenta}{∠EDC}}\,\)を引いた角も等しくなるので
　\(\begin{eqnarray}
\mathrm{\color{red}{∠ADE}}&=&\mathrm{∠ADC-\color{magenta}{∠EDC}}\\
&=&90^{\circ}-\color{magenta}{∠\mathrm{EDC}}　･･･③
\end{eqnarray}\)

　\(\begin{eqnarray}
\mathrm{\color{blue}{∠CDG}}&=&\mathrm{∠EDG-\color{magenta}{∠EDC}}\\
&=&90^{\circ}-\color{magenta}{∠\mathrm{EDC}}　･･･④
\end{eqnarray}\)
③④より
　\(\,\mathrm{\color{red}{∠ADE}=\color{blue}{∠CDG}}\,　･･･⑤\)
①②⑤から
　\(\underline{　2辺とその間の角　}\)がそれぞれ等しい
ので、
　\(\,\mathrm{△AED　≡　△CGD}\,\)

ここまではすぐに終わりますので、後は角度を求めるだけですが、
合同が示されたので\(\,\mathrm{∠DCG}\,\)は\(\,\mathrm{∠DAE}\,\)と等しいことが分かります。

合同な図形の対応する辺と角はそれぞれ等しいからですよ。　
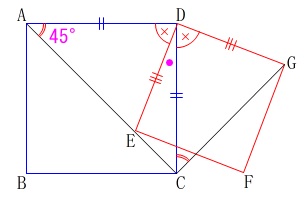辺\(\,\mathrm{AC}\,\)は正方形の対角線なので、
　
　\(\mathrm{∠CAD}=45^{\circ}\)

よって、

　\(\begin{eqnarray}
\mathrm{∠DCG}&=&\mathrm{∠DAE}\\
&=&\underline{　45^{\circ}　}
\end{eqnarray}\)

答え　\(\color{black}{\fbox{　Ⅰ　}}\)　\(\,\underline{　90　}\,\)　\(\color{black}{\fbox{　Ⅱ　}}\)　\(\,\underline{　45　}\,\)

こんなところで時間をかけている場合ではありません。
先に行きます。

(3)
さいころ２つの出目の積だけコマを進める問題です。

このような問題は、どのような動きをするか確認してからです。

あちこちの高校入試で出ていますが、2018年度の神奈川県の公立入試なんかが良い練習になりますよ。

⇒　神奈川県公立入試2018年(平成30年)の数学問5確率問題の解説

この問題だと、\(\,\mathrm{A}\,\)をスタート位置としてコマを順番に回していくと、

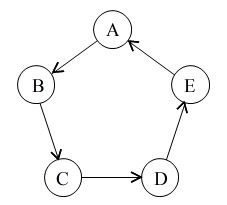
例えば、
コマが\(\,\mathrm{B}\,\)に止まるのは出目の積が

　\(\,1,6,11,16,21,26,31,36\,\)

のときで、\(\,5\,\)で割って\(\,1\,\)余る数の場合です。

（さいころの出目の積で出てこない数字もあります。）

同じ様に

　\(\,\mathrm{C}\,\)に止まるのは\(\,5\,\)で割って\(\,2\,\)余る数の場合
　\(\,\mathrm{D}\,\)に止まるのは\(\,5\,\)で割って\(\,3\,\)余る数の場合
　\(\,\mathrm{E}\,\)に止まるのは\(\,5\,\)で割って\(\,4\,\)余る数の場合
　\(\,\mathrm{A}\,\)に止まるのは\(\,5\,\)で割って\(\,0\,\)余る数の場合
（\(\,5\,\)で割って\(\,0\,\)余るというのは、\(\,5\,\)で割り切れる、ということです。）

この中では、さいころの出目の積だと\(\,5\,\)で割り切れる数が一番多くなりますが一応確認しておきましょう。

さいころ２つの場合は樹形図よりは表の方が見やすいですね。

大小どちらでも良いですが、大を赤、小を青で出目表を書くと
（表の中の数字はその積です。）

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\color{red}{1} & 1 & 2 & 3 & 4 & \color{magenta}{5} & 6 \\ \hline
\color{red}{2} & 2 & 4 & 6 & 8 & \color{magenta}{10} & 12 \\ \hline
\color{red}{3} & 3 & 6 & 9 & 12 & \color{magenta}{15} & 18 \\ \hline
\color{red}{4} & 4 & 8 & 12 & 16 & \color{magenta}{20} & 24 \\ \hline
\color{red}{5} & \color{magenta}{5} & \color{magenta}{10} & \color{magenta}{15} & \color{magenta}{20} & \color{magenta}{25} & \color{magenta}{30} \\ \hline
\color{red}{6} & 6 & 12 & 18 & 24 & \color{magenta}{30} & 36 \\ \hline
\end{array}\)

これをどこに止まるか記号で示してみると

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\color{red}{1} & B & C & D & E & \mathrm{\color{magenta}{A}} & B \\ \hline
\color{red}{2} & C & E & B & D & \mathrm{\color{magenta}{A}} & C \\ \hline
\color{red}{3} & D & B & E & C & \mathrm{\color{magenta}{A}} & D \\ \hline
\color{red}{4} & E & D & C & B & \mathrm{\color{magenta}{A}} & E \\ \hline
\color{red}{5} & \mathrm{\color{magenta}{A}} & \mathrm{\color{magenta}{A}} & \mathrm{\color{magenta}{A}} & \mathrm{\color{magenta}{A}} & \mathrm{\color{magenta}{A}} & \mathrm{\color{magenta}{A}} \\ \hline
\color{red}{6} & B & C & D & E & \mathrm{\color{magenta}{A}} & B \\ \hline
\end{array}\)

数えれば答えが出ます。

　答え　\(\,\underline{　ア　}\,\)　確率は　\(\displaystyle \underline{　\frac{11}{36}　}\)

きれいな計算だけで数学の答えが求まるわけではありません。
特に、場合の数や確率は調べ尽くす、という気持ちを持っておかないと答えは簡単でも、答えまでたどり着けない問題が増えてきていますよ。

(4)
電話料金の基本料金を変えてあります。
プランが3つありますので、通話する時間によってお得なプランを探そうという問題です。

　\(\,\mathrm{X}\,\)：\(\,30\,\)分まで通話料金は\(\,0\,\)円ですが、基本料金は\(\,1200\,\)円

\(\,1\,\)分も通話しなくても\(\,1200\,\)円がかかるプランです。

　\(\,\mathrm{Y}\,\)：\(\,60\,\)分まで通話料金は\(\,0\,\)円ですが、基本料金は\(\,2000\,\)円

\(\,1\,\)分も通話しなくても\(\,2000\,\)円かかりますますが、
ある程度通話する人にとっては\(\,\mathrm{X}\,\)プランよりも安くなります。

　\(\,\mathrm{Z}\,\)：通話時間関係なしに\(\,2800\,\)円

基本料金は\(\,\mathrm{X,Y}\,\)に比べて高いですが、通話時間がかなり多い人はこのプランの方が安くなります。

通話時間によってお得なプランが違います。
それを見比べてみようというのが問題です。

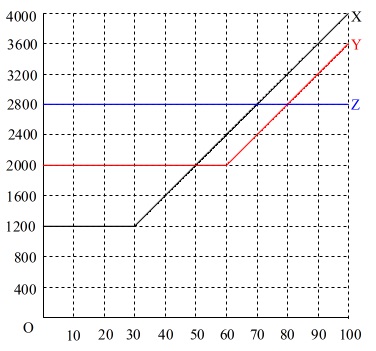
グラフですべて解決します。

①
プラン\(\,\mathrm{X}\,\)は\(\,30\,\)分までは\(\,1200\,\)円で一定、
それ以上通話時間があれば\(\,1\,\)分あたり\(\,40\,\)円追加されるので、
通話時間\(\,x\,\)と支払う料金\(\,y\,\)との関係は、
\(\,0≦x≦100\,\)においてグラフにすると
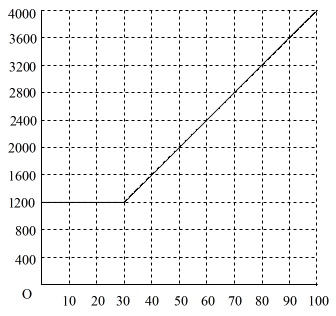これが答えです。

②
\(\,\mathrm{Y}\,\)プランが一番安い通話時間を求めます。

3つのプランのグラフを書いて、一番下になる部分が求める通話時間になります。

①で\(\,\mathrm{X}\,\)のグラフは書きました。
\(\,\mathrm{Y}\,\)と\(\,\mathrm{Z}\,\)の料金グラフを書き足します。

\(\,\mathrm{Y}\,\)プランは、
　\(\,60\,\)分まで\(\,2000\,\)円で一定で、
　その後\(\,1\,\)分ごとに\(\,40\,\)円ずつ料金が増します。

\(\,\mathrm{Z}\,\)プランは、
　\(\,2800\,\)円で料金は一定です。
この中で\(\,\mathrm{Y}\,\)プランが最も安い通話時間は、\(\,\mathrm{Y}\,\)プランが一番下になる部分で、

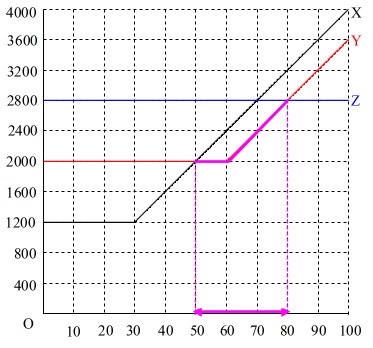
　\(\,\underline{　50　}\,\)分から\(\,\underline{　80　}\,\)分の間の通話時間