愛知県公立高校入試2019年A日程の数学問題と解説

愛知県で2019年(平成31年度)に行われた公立高校入試、全日制課程Aの数学問題と解説です。
大問は3問あり、第1問および第2問は小問集合、第3問は図形の総合問題です。
試験時間は45分ですが、時間が足りないと感じる人は時間配分に気をつけましょう。
第1問は基本問題の9問なのでできるだけ時間をかけずに済ませたい所です。

問題は愛知県が公表してくれています。
（昨年より公表が遅かったので解説が後になってしまいました。）

⇒　2019年度A日程数学問題

大問は\(\,3\,\)問ですが、内容は中学数学全部といって良いくらいバランスとボリュームのある問題なのできれいな解答を求めるより、思いついた方法が出てくれば突っ走って計算を素早く、確実にチャチャっと済ませましょう。

　\(\,\large{1}\,\)

(1)
計算の順序は（かっこ）の中からです。

　\(\hspace{10pt}8-(2-5)\\
=8-(-3)\\
=8+3\\
=\underline{　11　}\)

(2)
通分します。
『覚え太郎』会員は普通にしていることでしょうから何度も言うことになってクドいですが、
分数計算は分母を一つにすると分子の計算に集中できます。

　\(\hspace{10pt}\displaystyle \frac{5x+3}{3}-\frac{3x+2}{2}\\
\displaystyle =\frac{\color{red}{2}(5x+3)-\color{red}{3}(3x+2)}{\color{blue}{6}}\\
\displaystyle =\frac{10x+6-9x-6}{6}\\
\displaystyle =\underline{　\frac{x}{6}　}\)

答えは　\(\displaystyle \underline{　\frac{1}{6}\,x}　\)　でも同じですが、\(\,x\,\)は分子にあるので注意しておいて下さい。

多項式なら分子、単項式なら文字を横、と分けるより、いつも分子に文字式をおいておく方が分かり易いですが、どちらでも良いです。

(3)
無理数の計算です。
展開すれば良いだけですが、ルートの中は最も小さい数で答えるのが普通です。

　\(\hspace{10pt}\sqrt{3}(\sqrt{5}-3)+\sqrt{27}\\
=\sqrt{15}-3\sqrt{3}+3\sqrt{3}\\
=\underline{　\sqrt{15}　}\)

これ以上ルートの中は小さくならないので終わりです。

(4)
文字式の計算です。
割り算は逆数のかけ算なので割り算部分を分母に回して、いつも通り計算を進めましょう。

　\(\hspace{10pt}12x^2y\times (-3y)^2\color{red}{\div (2xy)^2}\\
\displaystyle =\frac{12x^2y\times (-3y)^2}{\color{red}{(2xy)^2}}\\
\displaystyle =\frac{12x^2y\times 9y^2}{4x^2y^2}\\
=\underline{　27y　}\)

(5)
方程式を解く基本は左辺にすべての項を集めて、右辺を\(\,0\,\)にすることです。
その後は左辺を因数分解できるか先に試しておきましょう。
できなければ解の公式ですが、すべてを解の公式で解こうとするのは効率悪いです。

　\(\begin{eqnarray}
(x+3)(x-8)+4(x+5)&=&0\\
x^2-5x-24+4x+20&=&0\\
x^2-x-4&=&0
\end{eqnarray}\)

因数分解できないので解の公式です。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-1)\pm \sqrt{(-1)^2-4\times 1\times (-4)}}{2}\\
&=&\frac{1\pm \sqrt{1+16}}{2}\\
&=&\frac{1\pm \sqrt{17}}{2}
\end{eqnarray}\)

解の公式については必ず使えるようになっておきましょう。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

解の公式の求め方は後回しで良いです。
公式は使えることが先でいいですよ。

(6)
文字式の関係を不等式で表します。

「切り取ることができる」

ということなので、もとのリボンの長さの方が長い、というだけです。

　\(\,x\,\mathrm{cm}\,\)のリボンから、
　\(\,15\,\mathrm{cm}\,\)のリボンを\(\,a\,\)本

切り取ることができるので、

　\(\,\underline{　x\,≧\,15a　}\,\)

(7)
変化の割合を求めます。

　\(\displaystyle \,\color{red}{(変化の割合)=\frac{　(\,y\,の増加量)　}{　(\,x\,の増加量)　}}\,\)

なので、\(\,x\,\)が\(\,4\,\)から\(\,6\,\)まで増加するときの\(\,y\,\)の増加量を求めれば良いのです。

関数は\(\displaystyle \,y=\frac{1}{2}x^2\,\)なので、

\(\,x=4\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (4)^2\\
&=&8
\end{eqnarray}\)

\(\,x=6\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (6)^2\\
&=&18
\end{eqnarray}\)

座標にすると分かり易いです。

　\(\,(\,\color{red}{4}\,,\,\color{blue}{8}\,)\,\)　\(\,(\,\color{red}{6}\,,\,\color{blue}{18}\,)\,\)

\(\,x\,\)の増加量は、\(\,\color{red}{6}-\color{red}{4}=\color{red}{2}\,\)

\(\,y\,\)の増加量は、\(\,\color{blue}{18}-\color{blue}{8}=\color{blue}{10}\,\)

よって変化の割合は

　\(\hspace{10pt}\displaystyle \frac{10}{2}=\underline{　5　}\)

増加量を求めるとき、引く方向は\(\,x\,\)と\(\,yで\,\)そろえないと符号が反対になるので気をつけましょう。
簡単なグラフを書けば、傾きの正負がはっきり見て取れるので確認すると良いです。

(8)
相対度数とは度数合計に対する割合のことです。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

度数分布表の中で説明していますので確認して下さい。

ここでは、

　\(\,7.4\,\)秒以上\(\,7.8\,\)秒未満の階級の相対度数が\(\,\color{red}{0.15}\,\)

度数合計は\(\,1\,\)年生の\(\,\color{blue}{120}\,\)人です。

よって、度数は

　\(\color{blue}{120}\times \color{red}{0.15}=\underline{　18　(人)}\)

(9)
相似な図形の長さを求める、よくある問題です。

条件

　\(\,\mathrm{AB}\, /\!/ \,\mathrm{EF}\, /\!/ \, \mathrm{DC}\,\)
　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{DC=4}\,\)
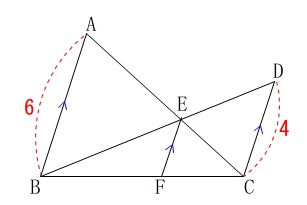平行線の同位角と錯角は等しいので、

　\(\,\mathrm{△ABE}\,\)　∽　\(\,\mathrm{△CDE}\,\)
　\(\,\mathrm{△BEF}\,\)　∽　\(\,\mathrm{△BDC}\,\)
　\(\,\mathrm{△CEF}\,\)　∽　\(\,\mathrm{△CAB}\,\)

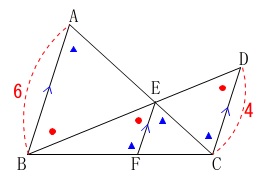
　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{DC=4}\,\)

なので、\(\,\mathrm{△BEF}\,\)と\(\,\mathrm{△BDC}\,\)の相似比は

　\(\,6:4=\color{blue}{3}:\color{blue}{2}\,\)
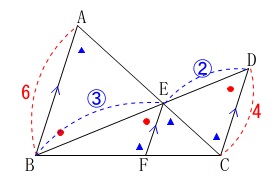このことから\(\,\mathrm{EF}\,\)は\(\,\mathrm{DC}\,\)の\(\displaystyle \,\color{blue}{\frac{3}{5}}\,\)なので、

　\(\begin{eqnarray}\displaystyle
\mathrm{EF}&=&4\times \color{blue}{\frac{3}{5}}\\
&=&\underline{　\frac{12}{5}　}
\end{eqnarray}\)

これは\(\,\mathrm{△CAB}\,\)で見て、

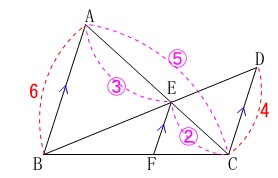
　\(\begin{eqnarray}\displaystyle
\mathrm{EF}&=&6\times \color{magenta}{\frac{2}{5}}\\
&=&\underline{　\frac{12}{5}　}
\end{eqnarray}\)