2020年(令和2年)広島県公立高校入試の数学の問題と解説

2020年(令和2年)に広島県で行われた公立高校入試の数学の問題と解説です。
問題は全分野から偏りなく、基本から標準までの問題で構成されています。
計算力に頼る問題はありませんので見直しまでを30分で終わらせることを目標にしてみてください。

※
広島県の公立高校入試では令和3年（2021年）度の削除項目はありません。
例年通り行うと発表されています。

2020年(令和2年)広島県公立高校入試の数学の問題

問題は広島県で公開されている形で添付しておきます。

⇒　令和２年度広島県公立高校入試の数学の問題

問題は例年通り基本から標準までの問題で大きく６問で構成されています。
平均点は\(\,50\,\)点満点中\(\,28.2\,\)点です。
\(\,2019\,\)年度は平均点が\(\,21.0\,\)点なので、
\(\,100点\,\)満点にすると\(\,14\,\)点以上上がっています。

2020年(令和2年)広島県公立高校入試の数学の解説

\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであります。

少し軽めの問題が多いので一気にいきます。
会員の目標は\(\,20\,\)分、見直しをていねいにしても\(\,30\,\)分で満点です。
（\(\,1\,\)題だけ答えに迷う問題があったので\(\,9\,\)割にしておきます。笑）
基本はできているはずなので手を止めないようにしましょう。

第１問基本の確認小問集合

\(\color{black}{\fbox{1}}\)

文字式を含む計算問題から因数分解、方程式、投影図、関数、確率の\(\,8\,\)題があります。

何もせずに答えが出る問題もありますが、
すべてに対して気を抜かないように自分で手を動かしましょう。
その分解説を簡潔にしておきます。笑

(1)
　\(\hspace{10pt}4+6\div (-3)\\
=4-2\\
=\underline{　2　}\)

割り算が先です。

(2)
　\(\hspace{10pt}4(2x-y)-(7x-3y)\\
=8x-4y-7x+3y\\
=\underline{　x-y　}\)

暗算で答えは出ますが、
\(\,2\,\)行目は省略しない方がミスが減ります。

(3)
因数分解です。

　\(\hspace{10pt}x^2+3x-28\\
=\underline{　(x-4)(x+7)　}\)

(4)
　\(\hspace{10pt}(\sqrt{2}+\sqrt{7})^2\\
=2+2\sqrt{14}+7\\
=\underline{　9+2\sqrt{14}　}\)

これも暗算できるでしょうけど、
確実にやっておきましょう。

(5)
\(\,2\,\)次方程式を解きます。
　\(\hspace{4pt}4x^2+7x+1=0\)
因数分解できないので解の公式ですね。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-7\pm \sqrt{7^2-4\times 4\times 1}}{2\times 4}\\
&=&\frac{-7\pm \sqrt{49-16}}{8}\\
&=&\underline{　\frac{-7\pm \sqrt{33}}{8}　}
\end{eqnarray}\)

(6)
投影図で与えられた図形の展開図を選びます。

図形は四角すいです。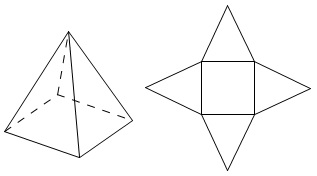展開図は底面の四角形1つと側面の三角形4つでできています。

答え　\(\,\underline{　②　}\,\)

立面図は真横から見た図、
平面図は真上から見た図です。

(7)
\(\,1\,\)辺\(\,x\,\)の正三角形の週の長さ\(\,y\,\)は
　\(\hspace{4pt}y=3x\)
です。

答え　\(\,\underline{　3　}\,\)

\(\,y=ax\,\)の比例定数は\(\,a\,\)のことです。

(8)
さいころ2つの確率です。

樹形図で良いですよ。
表でも同じですが、
2つのさいころの出方は\(\,36\,\)通り。
和が\(\,10\,\)になるのは
　\((\,大,小\,)=(4,6)\,,\,(5,5)\,,\,(6,4)\)
の\(\,3\,\)通りしかありません。

答え　\(\displaystyle \frac{3}{36}=\underline{　\frac{1}{12}　}\)

第２問文章を読み取る小問題集合

標本調査、対角線（三平方の定理）、方程式の\(\,3\,\)題があります。

(1)
国語辞典にある見出し語の総数を推測します。

手順が書いてありますがまとめると、
　\(\,10\,\)ページ分の見出し語を調べた。
　総ページは\(\,1452\,\)ページだった。

選んだページ番号は関係ありません。
平均を出す必要もありません。

調べた\(\,10\,\)ページの合計は\(\,10\,\)個の見出し語の数字を足して
　\(\hspace{10pt}57+43+\cdots +67+60\\
=560\)

この\(\,10\,\)ページ分の見出し語\(\,560\,\)と、
総ページ\(\,1452\,\)ページ分の見出し語の数\(\,x\,\)は比例関係にあると見なします。

　\(\begin{eqnarray}\displaystyle
10:560&=&1452:x\\
10x&=&1452\times 560\\
x&=&1452\times 56\\
&=&81312
\end{eqnarray}\)

これから、
　およそ\(\,81000\,\)語と推測できます。

答え　\(\,\underline{　③　}\,\)

ここでは比例式で求めましたが、
　\(\displaystyle 560\times \frac{1452}{10}=x\)
と比例計算しても良いですよ。

⇒　比例式の応用文章題への利用と便利な比の使い方

（比例関係は時計回りの計算になります。）

(2)
正方形が2つあって線分の長さが\(\,\sqrt{73}\,\)になるものを求めます。

　正方形\(\,\mathrm{ABCD}\,\)の\(\,1\,\)辺は\(\,3\,\)
　正方形\(\,\mathrm{ECFG}\,\)の\(\,1\,\)辺は\(\,5\,\)
（単位は\(\,\mathrm{cm}\,\)ですが省略します。）

\(\,\mathrm{CG=5\sqrt{2}=\color{red}{\sqrt{50}}}\,\)なので、
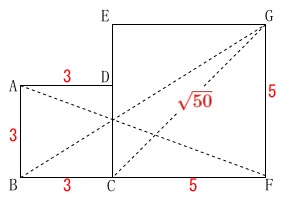それよりも長くなる\(\,\mathrm{AF}\,\)か\(\,\mathrm{BG}\,\)です。

　\(\begin{eqnarray}\displaystyle
\mathrm{AF}&=&\sqrt{3^2+(3+5)^2}\\
&=&\sqrt{9+64}\\
&=&\sqrt{73}
\end{eqnarray}\)

答え　\(\,\mathrm{\underline{　線分\,AF　}}\,\)

\(\,\mathrm{BF}\,\)から計算したとすると

　\(\begin{eqnarray}\displaystyle
\mathrm{BF}&=&\sqrt{5^2+8^2}\\
&=&\sqrt{25+64}\\
&=&\sqrt{89}
\end{eqnarray}\)

となるので\(\,\mathrm{AF}\,\)を後で計算することになります。
（それは私です。）

それぞれの平方を出しておいても良いですが、
　\(\,\mathrm{AB^2=9}\,\)
　\(\,\mathrm{BF^2=64}\,\)
　\(\,\mathrm{FG^2=25}\,\)
としている間に終わるので必要ありません。

(3)
道のりを求めます。

名前は誰でも良いので\(\,\mathrm{A}\,\)さんとなっています。

条件
　\(\,\mathrm{P,R,Q}\,\)の順に各地点があります。
　\(\,\mathrm{P}\,\)から\(\,\mathrm{Q}\,\)まで\(\,5200\,\)。
　\(\,\mathrm{P}\,\)から\(\,\mathrm{R}\,\)まで分速\(\,\mathrm{80}\,\)で移動。
　\(\,\mathrm{R}\,\)から\(\,\mathrm{Q}\,\)まで分速\(\,200\,\)で移動。
　全体で\(\,35\,\)分かかった。
（長さの単位は\(\,\mathrm{m}\,\)ですが省略しています。）
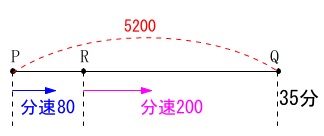\(\,1\,\)次方程式でも連立方程式でもどちらでも良いです。

知っているものは何でも使ってください。

両方やっておきます。

ⅰ)\(\,1\,\)次方程式で解く場合

　\(\,\mathrm{PR}=x\,\)とすると\(\,\mathrm{RQ}=5200-x\,\)とおける。
ただし、\(\,0\,≦\,x\,≦\,5200\,\)とする。
このとき
　\(\displaystyle \frac{x}{80}+\frac{5200-x}{200}=35\)
が成り立つのでこれを解いて
　\(\hspace{10pt}x=1200\)　（適）
よって、
　\(\,\mathrm{P}\,\)地点から\(\,\mathrm{R}\,\)地点まで\(\,1200\,\mathrm{m}\,\)
　\(\,\mathrm{R}\,\)地点から\(\,\mathrm{Q}\,\)地点まで\(\,4000\,\mathrm{m}\,\)
※
道のりなので直線とは限らないので、
求める課程を書く場合、
\(\,\mathrm{PR}\,\)などとしているところは、
「\(\,\mathrm{P}\,\)地点から\(\,\mathrm{R}\,\)地点までの道のり\(\,x\,\mathrm{m}\,\)とする。」
とした方が良いです。

ⅱ)連立方程式で解く場合

　\(\,\mathrm{PR}=x\,\)、\(\,\mathrm{RQ}=y\,\)とする。
ただし、\(\,0\,≦\,x\,≦\,5200\,\)とする。
このとき
　\( \begin{cases}
\hspace{4pt} x+y=5200\\
\hspace{4pt}\displaystyle \frac{x}{80}+\frac{y}{200}=35
\end{cases}\)
が成り立つのでこれを解いて
　\(\hspace{10pt}x=1200\,,\,y=4000\)　（適）
よって、
　\(\,\mathrm{P}\,\)地点から\(\,\mathrm{R}\,\)地点まで\(\,1200\,\mathrm{m}\,\)
　\(\,\mathrm{R}\,\)地点から\(\,\mathrm{Q}\,\)地点まで\(\,4000\,\mathrm{m}\,\)

どっちでも同じでしょう。

第３問度数折れ線と代表値および累積相対度数

\(\color{black}{\fbox{3}}\)
度数分布表と度数折れ線から最頻値と累積相対度数を求め比較します。

度数分布表と度数折れ線が読み取れれば会話はあまり気にしなくて良いです。
「天気予報によると次の日曜日は雨」
が探せたら大丈夫です。

(1)
度数分布表での最頻値は、
　度数が一番多い階級の階級値
になります。

休日の度数が一番多い階級は
　\(\,80\,\)分以上\(\,100\,\)分未満の階級
なので
　最頻値は\(\,\underline{　90　分}\,\)

階級の中央値が階級値です。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

度数分布表から代表値を求める方法は確認しておくと良いです。
新課程では累積度数や(2)の累積相対度数が入ってくるので出番が多くなります。

(2)
度数分布表から書いた度数折れ線を比較したけど、
似たような折れ線になったので度数分布表に戻ります。

日数の合計が違うので度数では比較できないから、
相対度数で比較しています。

待ち時間を\(\,40\,\)分未満に絞って累積相対度数（※）を比べると、
雨が降った休日の累積相対度数は
　\(\hspace{10pt}0.03+0.26\\
=0.29\)
雨が降らなかった平日の累積相対度数は
　\(\hspace{10pt}0.00+0.17\\
=0.17\)

天気予報通りなら、（予報では次の日曜日は雨）
次の日曜日の方が待ち時間が\(\,40\,\)分未満で済む可能性は高くなります。

答え　ア　\(\,\underline{　0.29　}\,\)　イ　\(\,\underline{　0.17　}\,\)　ウ　\(\,\underline{　①　}\,\)

※
累積相対度数とは、
小さい方からその階級までの相対度数の合計のことです。

文字が多くて読むのに疲れますが、
こういった問題は多くなっているので慣れておきましょう。

第４問文字式と証明

連続整数を文字式で扱う問題です。
(1)
【予想】は日本語で書かれていますが、
説明では文字式に換えてくれているのでそのまま計算すれば良いだけです。

連続\(\,4\,\)整数を
　\(n\,,\,n+1\,,\,n+2\,,\,n+3\)
とすると、
（ここから）
大きい方から\(\,1\,\)番目の数と大きい方から\(\,2\,\)番目の数の積から、
小さい方から\(\,1\,\)番目の数と\(\,2\,\)番目の数の積を引くと、
　\(\hspace{10pt}(n+3)(n+2)-n(n+1)\\
=n^2+5n+6-n^2-n\\
=4n+6\\
=n+(n+1)+(n+2)+(n+3)\)
これは連続する4つの整数の和になっている。
（ここまで）
この後「したがって」に続きます。

日本語で長々と書いてあることが文字式だと簡単に済むので便利ですよね。

(2)
連続する\(\,4\,\)整数について成り立つ(1)と違う性質と、
連続する\(\,5\,\)整数についての性質で、
共通する性質を考えます。

どちらも文字式を計算するだけです。

【性質\(\,\mathrm{Ⅰ}\,\)】
\(\,4\,\)連続整数は同じで
　\(\color{red}{n}\,,\,\color{blue}{n+1}\,,\,\color{blue}{n+2}\,,\,\color{red}{n+3}\)

連続する4つの整数について、
　小さい方から\(\,2\,\)番目の数\(\,\color{blue}{n+1}\,\)
と大きい方から\(\,1\,\)番目の数\(\,\color{red}{n+3}\,\)
の積
　\(\hspace{10pt}(\color{blue}{n+1})(\color{red}{n+3})\)
から
　小さい方から\(\,1\,\)番目の数\(\,\color{red}{n}\,\)
と大きい方から\(\,2\,\)番目の数\(\,\color{blue}{n+2}\,\)
の積
　\(\hspace{10pt}\color{red}{n}(\color{blue}{n+2})\)
の差は、
　\(\hspace{10pt}(\color{blue}{n+1})(\color{red}{n+3})-\color{red}{n}(\color{blue}{n+2})\\
=n^2+4n+3-n^2-2n\\
=2n+3\)

これが何の和になっているかです。

　\(\hspace{10pt}2n+3\\
=\color{red}{n}+(\color{red}{n+3})　･･･①\\
=(\color{blue}{n+1})+(\color{blue}{n+2})　･･･②\)

①は
　「小さい方から\(\,1\,\)番目の数と大きい方から\(\,1\,\)番目の数」の和
②は
　「小さい方から\(\,2\,\)番目の数と大きい方から\(\,2\,\)番目の数」の和
になっています。

【性質\(\,\mathrm{Ⅱ}\,\)】
\(\,5\,\)連続整数は
　\(\color{red}{m}\,,\,\color{blue}{m+1}\,,\,m+2\,,\,\color{blue}{m+3}\,,\,\color{red}{m+4}\)
と表すことができて、
　小さい方から\(\,2\,\)番目の数\(\,\color{blue}{m+1}\,\)
と大きい方から\(\,1\,\)番目の数\(\,\color{red}{m+4}\,\)
の積
　\(\hspace{10pt}(\color{blue}{m+1})(\color{red}{m+4})\)
から
　小さい方から\(\,1\,\)番目の数\(\,\color{red}{m}\,\)
と大きい方から\(\,2\,\)番目の数\(\,\color{blue}{m+3}\,\)
の積
　\(\hspace{10pt}m(m+3)\)
の差は
　\(\hspace{10pt}(\color{blue}{m+1})(\color{red}{m+4})-\color{red}{m}(\color{blue}{m+3})\\
=m^2+5m+4-m^2-3m\\
=2m+4\\
=\color{red}{m}+(\color{red}{m+4})　･･･③\\
=(\color{blue}{m+1})+(\color{blue}{m+3})　･･･④\\
=(m+2)+(m+2)　･･･⑤\)

①②と③④⑤で同じ表現になるのは、

　①と③の
　「小さい方から\(\,1\,\)番目の数と大きい方から\(\,1\,\)番目の数の和」
または
　②と④の
　「小さい方から\(\,2\,\)番目の数と大きい方から\(\,2\,\)番目の数の和」

のどちらかですね。
解答を1つに絞るには条件が足りません。
私が解答するなら「または」で両方書いておきます。
何か条件見逃したかな？

このことは何個の連続整数でも一般的に終えることなので、
小さい順に
　\(\,1\,\)番目と最後の整数の和
　\(\,2\,\)番目と最後から\(\,2\,\)番目の整数の和
　\(\,\cdots\,\)
となります。

連続整数を
　\(\color{red}{n}\,,\,\color{blue}{n+1}\,,\,\color{magenta}{n+2}\,,\,\cdots \,\color{magenta}{n+m-2}\,,\,\color{blue}{n+m-1}\,,\,\color{red}{n+m}\)
とすると
　\(\hspace{10pt}(\color{blue}{n+1})(\color{red}{n+m})-\color{red}{n}(\color{blue}{n+m-1})\\
=n^2+nm+n+m-n^2-nm+n\\
=2n+m\\
=\color{red}{n}+(\color{red}{n+m})\\
=(\color{blue}{n+1})+(\color{blue}{n+m-1})\\
=(\color{magenta}{n+2})+(\color{magenta}{n+m-2})\\
=\cdots \)

何をやっているか分からない人は、
見なかったことにしてください。

第５問合同の証明

\(\color{black}{\fbox{5}}\)

合同の証明です。

条件
　\(\,\mathrm{∠AOB=90^{\circ}}\,\)
　\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AC}}\,=\,\stackrel{\large{\frown}}{\mbox{BD}}}\,\)
　\(\,\mathrm{AO}\,\)⊥\(\,\mathrm{CE}\,\)
　\(\,\mathrm{AO}\,\)⊥\(\,\mathrm{DF}\,\)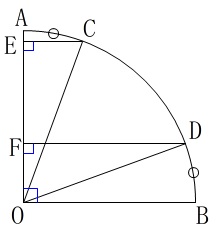証明は図の中で終わらせておく、ですよ。
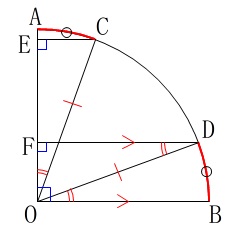平行線の錯角が見えた時点で終わりです。

（証明）
　\(\,\mathrm{△COE}\,\)と\(\,\mathrm{△ODF}\,\)において
仮定から
　\(\,\mathrm{∠OEC=∠DFO=90^{\circ}　･･･①}\,\)
同じ円の半径で等しくなるから
　\(\,\mathrm{CO=OD}　･･･②\)
また、同一長の弧に対する中心角は等しいので
　\(\mathrm{∠COE}=\mathrm{\color{blue}{∠BOD}}　･･･③\)
仮定から
　\(\,\mathrm{FD}\,\)∥\(\,\mathrm{OB}\,\)
だから、錯角は等しく
　\(\mathrm{∠ODF}=\mathrm{\color{blue}{∠BOD}}　･･･④\)
③④から
　\(\mathrm{∠COE=∠ODF}　･･･⑤\)
①②⑤より
　直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
よって、
　\(\,\mathrm{△COE}\,\)≡\(\,\mathrm{△ODF}\,\)
（終わり）

平行線の錯角を使いましたが、
解答例のように\(\,\mathrm{∠AOB=90^{\circ}}\,\)なので、
三角形の内角の和と合わせて考え、適当な角度を引いて
　\(\,\mathrm{∠OCE=∠DOF}\,\)
をいっても良いですよ。

第６問関数の性質と面積

\(\color{black}{\fbox{6}}\)

条件をしっかり抜き出せば普通の関数の問題です。

条件
　放物線は\(\,y=x^2\,\)
　点\(\,\mathrm{A\,(\,2\,,\,4\,)}\,\)
　点\(\,\mathrm{B}\,\)は点\(\,\mathrm{A}\,\)より上にある。
　点\(\,\mathrm{D,C}\,\)は\(\,x\,\)軸に平行で\(\,\mathrm{B}\,\)を通る。
　直線\(\,\mathrm{CA}\,\)と\(\,x\,\)軸の交点\(\,\mathrm{E}\,\)がある。
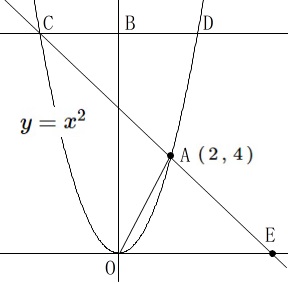\(\,\mathrm{A}\,\)は関数上の定点です。

(1)
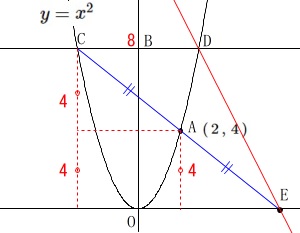
点\(\,\mathrm{E}\,\)の\(\,x\,\)座標が\(\,5\,\)のときの\(\,\mathrm{△AOE}\,\)の面積を求めます。
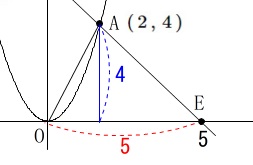他の点に関係なく\(\,\mathrm{A}\,\)は定点なので\(\,\mathrm{E}\,\)の\(\,x\,\)座標が\(\,5\,\)のとき、
\(\,\mathrm{△AOE}\,\)の面積は底辺を\(\,\mathrm{\color{red}{OE}}\,\)、
高さを\(\,\mathrm{A}\,\)の\(\,y\,\)座標\(\,\color{blue}{4}\,\)とみることができるので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△AOE}&=&\frac{1}{2}\times \color{red}{5}\times \color{blue}{4}\\
&=&\underline{　10　}
\end{eqnarray}\)

(2)
直線\(\,\mathrm{DE}\,\)の傾きを求めます。

条件が加わります。

条件
　\(\,\mathrm{CA＝AE}\,\)
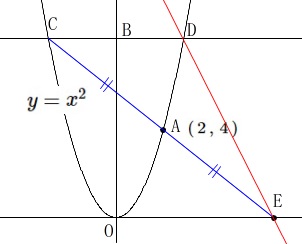点\(\,\mathrm{A}\,\)が線分\(\,\mathrm{CE}\,\)の中点なので、
点\(\,\mathrm{C,B,D}\,\)の\(\,y\,\)座標は\(\,8\,\)であることは確認しておきましょう。
これから具体的に\(\,\mathrm{C,D,E}\,\)の座標を出して、
直線\(\,\mathrm{DE}\,\)傾きを計算しても良いです。
時間は余っているだろうから突っ走っても大丈夫です。

\(\,\mathrm{C,D}\,\)の\(\,x\,\)座標は、
\(\,y\,\)座標が\(\,\color{red}{8}\,\)であることから
　\(\begin{eqnarray}\displaystyle
x^2&=&8\\
x&=&\pm 2\sqrt{2}
\end{eqnarray}\)

これから
　\(\,\mathrm{C}\,\,(\,-2\sqrt{2}\,,\,8\,)\)
　\(\,\mathrm{D}\,\,(\,\color{red}{2\sqrt{2}}\,,\,\color{red}{8}\,)\)
　\(\,\mathrm{E}\,\,(\,\color{blue}{4+2\sqrt{2}}\,,\,\color{blue}{0}\,)\)
です。

よって直線\(\,\mathrm{DE}\,\)の傾きは
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{0}-\color{red}{8}}{\color{blue}{4+2\sqrt{2}}-\color{red}{2\sqrt{2}}}\\
\displaystyle =\frac{-8}{4}\\
=\underline{　-2　}\)

しかし、座標設定した人が多いと思うので\(\,2\,\)通り示しておきます。

ⅰ）点\(\,\mathrm{E}\,\)を\(\,(\,t\,,\,0\,)\,\)とおいた場合

\(\,\mathrm{AE}\,\)間の\(\,x\,\)座標の差は\(\,\color{blue}{t-2}\,\)なので、
\(\,\mathrm{AC}\,\)間の\(\,x\,\)座標の差も\(\,\color{blue}{t-2}\,\)だから
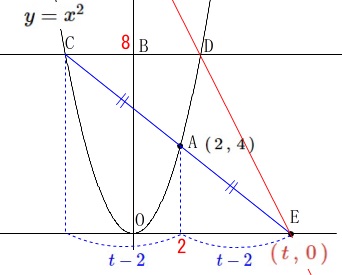点\(\,\mathrm{C}\,\)の\(\,x\,\)座標は
　\(\hspace{10pt}2-(\color{blue}{t-2})=\color{magenta}{4-t}\)

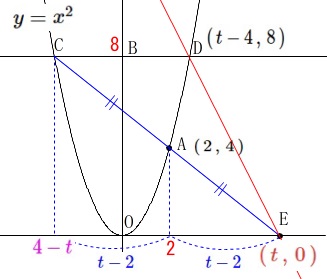
このとき\(\,\mathrm{D}\,\)の\(\,x\,\)座標は、
\(\,\mathrm{C}\,\)と符号が逆になるので
（\(\,y\,\)軸対称だから）
\(\,\mathrm{D}\,\)の座標は
　\(\,\mathrm{D}\,(\,t-4\,,\,8\,)\,\)
よって、
　\(\,\mathrm{D}\,(\,\color{red}{t-4}\,,\,\color{red}{8}\,)\,\)
　\(\,\mathrm{E}\,(\,\color{blue}{t}\,,\,\color{blue}{0}\,)\,\)
を通る直線の傾きは
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{0}-\color{red}{8}}{\color{blue}{t}-(\color{red}{t-4})}\\
\displaystyle =\frac{-8}{4}\\
=\underline{　-2　}\)

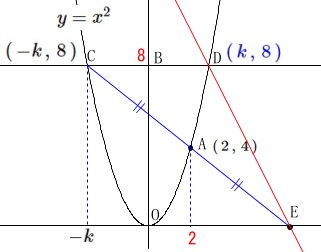
ⅱ）点\(\,\mathrm{D}\,\)の座標を\(\,(\,k\,,\,8\,)\,\)とおいた場合

点\(\,\mathrm{C}\,\)の座標は
　\(\,\mathrm{C}\,(\,-k\,,\,8\,)\,\)
\(\,2\,\)点\(\,\mathrm{AC}\,\)間の\(\,x\,\)座標の差は
　\(2-(-k)=\color{magenta}{k+2}\)
なので\(\,\mathrm{AE}\,\)間の\(\,x\,\)座標の差も\(\,\color{magenta}{k+2}\,\)だから
　\(\,\mathrm{E}\,(\,k+4\,,\,0\,)\,\)
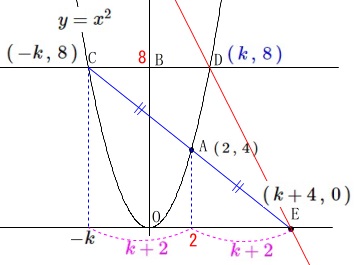よって、求める直線\(\,\mathrm{DE}\,\)の傾きは
　\(\,\mathrm{D}\,(\,\color{red}{k}\,,\,\color{red}{8}\,)\,\)
　\(\,\mathrm{E}\,(\,\color{blue}{k+4}\,,\,\color{blue}{0}\,)\,\)
から
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{0}-\color{red}{8}}{(\color{blue}{k+4})-\color{red}{k}}\\
\displaystyle =\frac{-8}{4}\\
=\underline{　-2　}\)