2018年（平成30年）度に広島県で行われた公立高校入試数学の問題と解説です。
問題は1から6までありますが基本から標準までの問題構成なので一気に説明します。
標準的な問題ではありますが、単純に公式を利用するだけの問題ではないので条件はよく見ておきましょう。
数学の教科書にある基本的な内容を理解しているか確認するには良い問題です。
2018年（平成30年）度広島県公立高校入試の数学の問題
問題は広島県で公開されています。
2018年（平成30年）度広島県公立高校入試の数学の解説
\(\color{black}{\fbox{ 1 }}\)は基本の小問集合ですが配点は大きいです。
式の計算や方程式、図形、近似値、関数の小問集合
\(\color{black}{\fbox{ 1 }}\)
(1)
乗法（かけ算）と除法（割り算）において、
負の数が偶数回のときは積と商は正の数になります。
\(\hspace{10pt}(-56)\div (-8)\\
=\underline{ 7 }\)
もちろん割り算は逆数のかけ算ですべて計算できるので、
\(\hspace{10pt}(-56)\div (-8)\\
\displaystyle =\frac{56}{8} (符号は＋になるのでいらない)\\
=\underline{ 7 }\)
としておくとややこしい計算でも同じように計算できます。
加法（足し算）の＋や減法（引き算）の－が計算途中に入るとそこで計算が途切れるというのは説明はいらないですね。
(2)
文字式の計算です。
展開して同類項をまとめるだけです。
\(\hspace{10pt}2(3x+y)+(4x-y)\\
=6x+2y+4x-y\\
=\underline{ 10x+y }\)
\(\,2\,\)行目の（かっこ）を外す\(\,1\,\)行を書くことでミスは減りますよ。
(3)
無理数の計算ですが展開公式を使うことできれいな数になります。
\(\hspace{10pt}(\sqrt{13}+2)(\sqrt{13}-2)\\
=(\sqrt{13})^2-2^2\\
=13-4\\
=\underline{ 9 }\)
展開公式
\(\color{red}{(a+b)(a-b)=a^2-b^2}\)
を利用しています。
展開は公式を覚えていなくても地道に展開すれば、
\(\hspace{10pt}(\sqrt{13}+2)(\sqrt{13}-2)\\
=(\sqrt{13})^2-2\sqrt{13}+2\sqrt{13}-2^2\\
=13-4\\
=\underline{ 9 }\)
答えは出ますが、公式利用すると計算結果は早く、楽にでますよ。
(4)
\(\,1\,\)次方程式を立式して解を求めます。
等式の関係は、等しいものを並べるだけなので、何が変化していないか考えれば方程式は立式しやすいです。
ここで変化していないのは、「生徒数」と「りんごの総数」です。
生徒数を求めるので生徒数を\(\,x\,\)としてりんごの総数で方程式を立てましょう。
\(\,1\,\)人に\(\,8\,\)個ずつ配ると\(\,8x\,\)のりんごが必要ですが\(\,5\,\)個不足しているので、
りんごの総数は、
\(\color{red}{8x-5} ･･･①\)
また、\(\,1\,\)人に\(\,7\,\)個ずつ配ると\(\,7x\,\)のりんごが必要ですが\(\,9\,\)個余るので、
りんごの総数は、
\(\color{blue}{7x+9} ･･･②\)
りんごの総数は変化していないので、①と②は等しいから
\(\begin{eqnarray}
\color{red}{8x-5}&=&\color{blue}{7x+9}\\
8x-7x&=&9+5\\
x&=&\underline{ 14 } (人)
\end{eqnarray}\)
(5)
数学では単に対称といえば線対称を意味します。
ここでは対称の軸が\(\,\ell\,\)です。
線対称では元の点と移動した点を結んだ線分の垂直二等分線が軸になりますので、
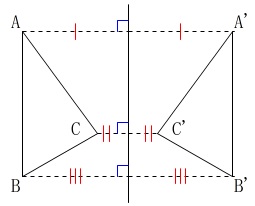
方眼を利用しなくてもコンパスと定規でかけるようになっておくと良いです。
ここでは方眼の目盛りを利用して移動させるだけです。
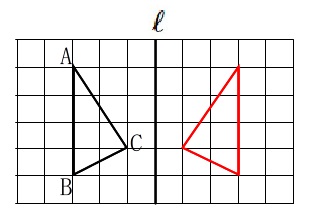
(6)
円錐（すい）の体積です。
錐体の体積\(\,\mathrm{V}\,\)は底面積を\(\,\mathrm{S}\,\)、高さを\(\,h\,\)とすると、
\(\displaystyle \color{red}{\mathrm{V}=\frac{1}{3}\,\mathrm{S}\,h}\)
です。
⇒ 円錐(すい)の表面積や四角錐,五角錐の体積の求め方2019年3月15日
底面の円の半径が\(\,\color{blue}{5}\,\)なので、底面積\(\,\mathrm{S}\,\)は
\(\begin{eqnarray}
\mathrm{S}&=&\pi\,(\color{blue}{5})^2\\
&=&25\,\pi (\mathrm{cm^2})
\end{eqnarray}\)
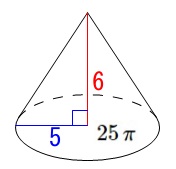
高さも\(\,\color{red}{6}\,\)と問題に書いてくれているので、そのまま公式に代入しましょう。
\(\begin{eqnarray}
\mathrm{V}&=&\frac{1}{3}\times 25\,\pi\times \color{red}{6}\\
&=&\underline{ 50\,\pi } (\,\mathrm{cm^3}\,)
\end{eqnarray}\)
(7)
単なる四捨五入です。
真の値からのズレは「誤差」ですね。
\(\underline{ 36.35\,≦\,a\,＜\,36.45 }\)
⇒ 近似値とは？誤差の大きさと真の値の範囲の表し方(中１資料の活用)
こちらも見ておくと良いでしょう。
⇒ 有効数字とは？桁(けた)数と四捨五入の方法と表し方(中1資料)
四則演算における有効数字の使い方は高校の理科で詳しくやることになります。
ただし、有効数字と誤差そのものは中学の間にしっかり覚えておきましょう。
(8)
決められた\(\,x\,\)の範囲で単調増加する関数を選びます。
簡単に言えば、グラフを見て、
指定された\(\,x\,\)の範囲で、
右に行けば\(\,y\,\)の値が増えている関数
を選ぶということです。
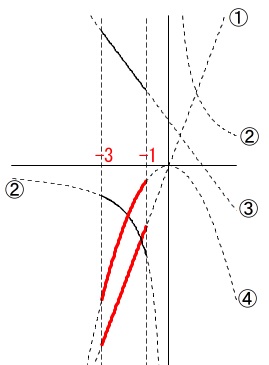\(-3≦x≦-1\)の範囲で右に行けば増加しているのは、
答え \(\underline{ ① と ④ }\)
\(\color{black}{\fbox{ 1 }}\)はここまでですが、
配点が\(\,50\,\)点満点中\(\,16\,\)点分、
\(\,100\,\)点満点で考えると\(\,32\,\)点分ありますよ。
次は \(\color{black}{\fbox{ 2 }}\) です。
確率、1次関数、文字式の利用
\(\color{black}{\fbox{ 2 }}\)
(1)
「確率が同じものを選べ」ということですので、
確率をすべて求めれば答えはすぐに出ます。
①
男子が選ばれる確率は \(\displaystyle\frac{2}{5}\)
女子が選ばれる確率は \(\displaystyle\frac{3}{5}\)
②
表が出る確率は \(\displaystyle\frac{1}{2}\)
裏が出る確率は \(\displaystyle\frac{1}{2}\)
③
\(\color{black}{\fbox{ ● }}\)が取り出される確率は \(\displaystyle\frac{1}{3}\)
\(\color{black}{\fbox{ ★ }}\)が取り出される確率は \(\displaystyle\frac{1}{3}\)
④
\(\,4\,\)の目が出る確率は \(\displaystyle\frac{1}{6}\)
\(\,4\,\)以外の目が出る確率は \(\displaystyle\frac{5}{6}\)
答え \(\,\underline{ ② , ③ }\,\)
(2)
点が移動するときの三角形の面積の変化をグラフに示す問題ですが、
高さが一定なので\(\,1\,\)次関数になります。
底辺\(\,\mathrm{BC}\,\)上の点\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)から\(\,\mathrm{C}\,\)まで移動するときなので、
定義域（\(\,x\,\)の変域）は、
\(0≦x≦15\)
この範囲のグラフを書きます。
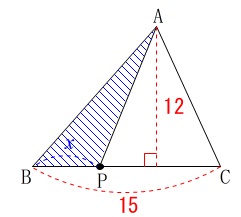点\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)にあるとき\(\,x=0\,\)で三角形にはなりませんが、
そのときの面積\(\,y\,\)は\(\,0\,\)とすると問題に書いてあるので原点からつなげば良いです。
底辺\(\,\mathrm{BP}=x\,\)
高さ\(\,\mathrm{12}\,\)
なので\(\,\mathrm{△ABP}\,\)の面積\(\,y\,\)は、
\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times x\times 12\\
&=&6x (\,0\,≦\,x\,≦\,15\,)
\end{eqnarray}\)
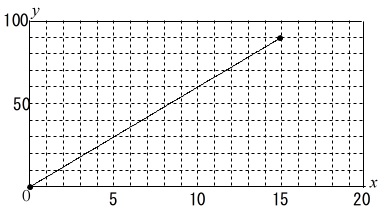
この比例のグラフの一部
\(\,x=0\,\) のとき \(\,y=0\,\)
\(\,x=15\,\) のとき \(\,y=90\,\)
の\(\,2\,\)点を通る線分が答えです。
(3)
数字をこねくり回して元に戻るよくある問題です。
手順通りに文字式を作っていけば自然に求まりますが、
文字式で表せないと話になりません。
⇒ 中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)
ここで扱うのは\(\,2\,\)桁の自然数だけですね。
手順〔\(\,1\,\)〕
思い浮かべた自然数を\(\,\color{red}{x}\,\)とします。
手順〔\(\,2\,\)〕
十の位が\(\,2\,\)の自然数を選びます。
一の位の数を\(\,y\,\)とすると
\(\color{blue}{20+y}\)
手順〔\(\,3\,\)〕
\(\,\color{blue}{20+y}\,\)の各桁の数をたします。
\(\color{magenta}{2+y}\)
手順〔\(\,4\,\)〕
\(\color{magenta}{2+y}\,\)に\(\,\color{red}{x}\,\)を足します。
\(\color{magenta}{2+y}+\color{red}{x}\)
手順〔\(\,5\,\)〕
\(\color{magenta}{2+y}+\color{red}{x}\,\)から\(\,\color{blue}{20+y}\,\)を引きます。
\(\hspace{10pt}(\color{magenta}{2+y}+\color{red}{x})-(\color{blue}{20+y})\\
=\color{red}{x}-18\)
手順〔\(\,6\,\)〕
\(\color{red}{x}-18\,\)に\(\,18\,\)を足します。
\(\hspace{10pt}\color{red}{x}-18+18\\
=\color{red}{x}\)
はい、元の思い浮かべた自然数が出てきました。
あ、【健太さんの説明】では思い浮かべた数を\(\,\color{red}{a}\,\)、\(\,2\,\)桁の数の一の位の数を\(\,\color{blue}{b}\,\)としていますので、
解答では\(\,x,y\,\)ではなく\(\,a,b\,\)に置きかえてください。
\(\color{black}{\fbox{ 2 }}\) は以上です。
次に位行きましょう。
円柱の体積比較と相似
\(\color{black}{\fbox{ 3 }}\)
若葉さんと春香さんが飲料水を入れる容器のことで話し合っていますが、
円柱と傾けたときに中に入る水の容積の問題です。
底面の直径は同じなので底面積は同じです。
高さは高い方が容積は大きくなりますが、水道の蛇口までの高さが邪魔をするので高ければ多く入れることができるとは限りません。
もちろん、入るだけいれて、最後に少し注ぎ足すのなら、高さが高い方が容量は大きいです。
ここでは注ぎ足すことはしないで、斜めのままの状態で入る水の容積を比べます。
体積の比較ですが、断面を見た平面で比較できます。
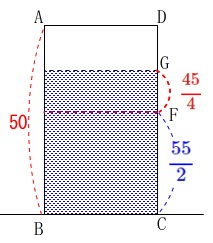
【図と説明】にある条件を抜き出して見ましょう。
\(\,\mathrm{ABCD}\,\)は長方形
\(\,\mathrm{AB=50}\,\)
\(\,\mathrm{AD=30}\,\)
\(\,\mathrm{∠AEB=90^{\circ}}\,\)
\(\,\mathrm{AE=40}\,\)
\(\,\mathrm{AF} \,/\!/\,\mathrm{EB}\,\)
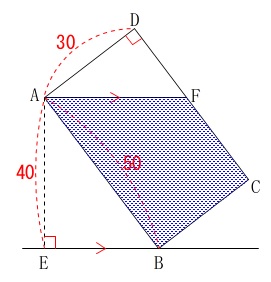\(\,\mathrm{△AEB}\,\)は直角三角形なので、三平方の定理が使えます。
(1)
\(\,\mathrm{BE}\,\)の長さは\(\,\mathrm{△ABE}\,\)に三平方の定理を利用して、
\(\begin{eqnarray}
\mathrm{AE^2+BE^2}&=&\mathrm{AB^2}\\
40^2+\mathrm{BE^2}&=&50^2\\
\mathrm{BE^2}&=&2500-1600\\
&=&900\\
\mathrm{BE}&=&\pm \,30
\end{eqnarray}\)
\(\,\mathrm{BE}\,\)は長さなので\(\,\mathrm{BE\,＞\,0}\,\)だから
\(\mathrm{BE}=\underline{ 30 } (\mathrm{cm})\)
(2)
斜めに注いだ水の入った容器をまっすぐにに起こすと水面はどこになるかです。
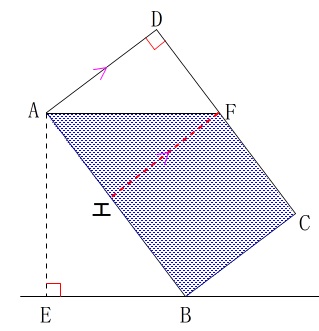\(\,\mathrm{F}\,\)から\(\,\mathrm{AD}\,\)に平行線を引くとエになります。
立て直すと、赤い斜線部分の水が動くと考えると水面の高さは、
赤い部分の水の体積と上の白い部分の体積が同じなので、中間の高さで水平になります。
つまり、\(\,\mathrm{DF}\,\)の中点になります。
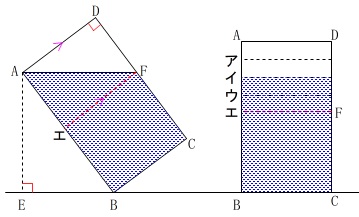
答え \(\,\underline{ イ }\,\)
(3)
容器\(\,a\,\)よりも容器\(\,b\,\)の方が水面が高くなると判断できる理由です。
つまり、底面積が同じなので、
斜めにしなければいけない高さ\(\,50\,\)の容器よりも、
斜めにせずに水が入れることができる高さ\(\,40\,\)の容器の方が
多くの水が入るという理由です。
\(\,\mathrm{△AEB}\,\) ∽ \(\,\mathrm{△ADF}\,\)であることは証明しなくて良い、と書いてあるので相似を使います。
使わないならわざわざ問題に書いたりしませんからね。
線分\(\,\mathrm{BE}\,\)の長さは(1)で求めています。
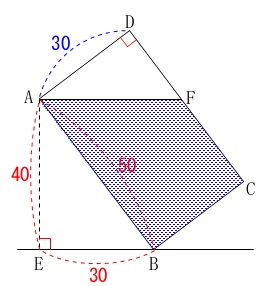\(\,\mathrm{△AEB}\,\) ∽ \(\,\mathrm{△ADF}\,\)なので、
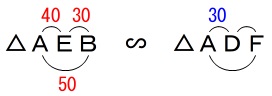比例式から\(\,\mathrm{DF}\,\)を求めます。
\(\begin{eqnarray}\displaystyle
\mathrm{AE:AD}&=&\mathrm{EB:DF}\\
\mathrm{AE} \times \mathrm{DF}&=&\mathrm{AD}\times \mathrm{EB}\\
40\times \mathrm{DF}&=&30\times 30\\
\mathrm{DF}&=&\frac{30\times 30}{40}\\
&=&\color{magenta}{\frac{45}{2}}
\end{eqnarray}\)
このとき\(\,\mathrm{CF}\,\)の長さも分かります。
\(\begin{eqnarray}
\mathrm{CF}&=&\mathrm{DC-DF}\\
&=&50-\color{magenta}{\frac{45}{2}}\\
&=&\color{blue}{\frac{55}{2}}
\end{eqnarray}\)
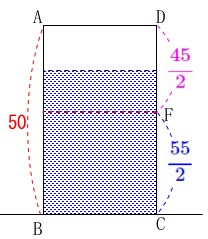
また、(2)で\(\,a\,\)の水面は\(\,\mathrm{DF}\,\)の中点になることが分かっているので、
水面となる\(\,\mathrm{DC}\,\)上の点を\(\,\mathrm{G}\,\)とすると、
\(\begin{eqnarray}\displaystyle
\mathrm{GF}&=&\frac{1}{2}\times \mathrm{DF}\\
&=&\frac{1}{2}\times \frac{45}{2}\\
&=&\color{red}{\frac{45}{4}}
\end{eqnarray}\)
よって、容器\(\,a\,\)に水を注いだ後の水面の高さは、
\(\begin{eqnarray}\displaystyle
\mathrm{CG}&=&\mathrm{CF+FG}\\
&=&\color{blue}{\frac{55}{2}}+\color{red}{\frac{45}{4}}\\
&=&\frac{110+45}{4}\\
&=&\frac{155}{4}
\end{eqnarray}\)
これは容器\(\,b\,\)の高さ\(\,\displaystyle 40=\frac{160}{4}\,\)よりも低いので、
容器\(\,b\,\)の方が容器\(\,a\,\)よりも地面から水面までの高さが高いと判断できます。
\(\color{black}{\fbox{ 3 }}\)は以上です。
次に行きます。
1次関数と連立方程式
\(\color{black}{\fbox{ 4 }}\)
\(\color{black}{\fbox{ 4 }}\)が一番間違えやすい問題かもしれません。
基準になる年度（西暦）を必ず確認しておきましょう。
\(\,\mathrm{A}\,\)国と\(\,\mathrm{B}\,\)国との平均寿命\(\,y\,\)の推移を経過年数\(\,x\,\)として見ていますが、
基準になっているのは\(\,1985\,\)年です。
\(\,x\,\)と\(\,y\,\)の関係は、\(\,x=0\,\)となっているのが\(\,1985\,\)年だということです。
このことさえ忘れずに見ておけば、単なる\(\,1\,\)次関数の問題です。
利用するのは表の\(\,1\,\)と\(\,2\,\)だけです。
表\(\,1\,\)から\(\,\mathrm{A}\,\)国の\(\,x,y\,\)の関係式は、
\(\,2\,\)点\(\,(\,0\,,\,77.8\,)\,(\,24\,,\,82.6\,)\)を通る直線の方程式
で、
\(\,x\,\)の増加量が\(\,24-0=\color{red}{24}\,\)
\(\,y\,\)の増加量が\(\,82.6-77.8=\color{blue}{4.8}\,\)
だから、求める直線の傾きは
\(\displaystyle \frac{\color{blue}{4.8}}{\color{red}{24}}=\frac{1}{5}\)
切片は\(\,77.8\,\)なので
\(\displaystyle y=\frac{1}{5}x+77.8 ･･･①\)
\(\,2030\,\)年は
\(\,2030-1985=45\,\)
から\(\,x=45\,\)に相当するので、
\(\,2030\,\)年の\(\,\mathrm{A}\,\)国の平均寿命は、
\(\begin{eqnarray}\displaystyle y&=&\frac{1}{5}\times (45)+77.8\\
&=&9+77.8\\
&=&86.8
\end{eqnarray}\)
\(\color{black}{\fbox{ ア }}\) \(\,\underline{ 86.8 }\,\)
表\(\,2\,\)から\(\,\mathrm{B}\,\)国の\(\,x,y\,\)の関係式は、
\(\,2\,\)点\(\,(\,3\,,\,74.9\,)\,(\,22\,,\,80.6\,)\)を通る直線の方程式
で、
\(\,x\,\)の増加量が\(\,22-3=\color{red}{19}\,\)
\(\,y\,\)の増加量が\(\,80.6-74.9=\color{blue}{5.7}\,\)
だから、求める直線の傾きは
\(\displaystyle \frac{\color{blue}{5.7}}{\color{red}{19}}=\frac{3}{10}\)
となり、\(\,\displaystyle y=\frac{3}{10}x+b\,\)とおけます。
\(\,(\,3\,,\,74.9\,)\,(\,22\,,\,80.6\,)\)
のどちらかを代入すれば\(\,y\,\)切片の\(\,b\,\)が求まります。
ここでは\(\,(\,3\,,\,74.9\,)\,\)を代入します。
\(\begin{eqnarray}
74.9&=&\frac{3}{10}\times (3)+b\\
749&=&9+10\,b\\
10\,b&=&749-9\\
&=&740\\
b&=&74
\end{eqnarray}\)
よって\(\,\mathrm{B}\,\)国の平均寿命\(\,y\,\)と経過年数\(\,x\,\)との関係は
\(\displaystyle y=\frac{3}{10}x+74 ･･･②\)
\(\color{black}{\fbox{ イ }}\) \(\displaystyle \underline{ y=\frac{3}{10}x+74 }\)
「\(\,\mathrm{B}\,\)国の平均寿命が\(\,\mathrm{A}\,\)国に追いつく」
ということは、
①と②の\(\,y\,\)座標が同じになる
ということです。
連立方程式を解けば答えが出ますが、注意点が1つあります。
\( \begin{cases}
\displaystyle \hspace{7pt} y=\frac{3}{10}x+74\\ \\
\displaystyle \hspace{7pt} y=\frac{1}{5}x+77.8
\end{cases}\)
左辺が等しいので右辺どうしも等しいから、
\(\begin{eqnarray}\displaystyle
\frac{3}{10}x+74&=&\frac{1}{5}x+77.8\\
3x+740&=&2x+778\\
x&=&\color{red}{38}
\end{eqnarray}\)
平均寿命\(\,y\,\)を出す必要はありませんのでこれを答えとしたいところですが、
\(\,x\,\)は\(\,1985\,\)年を基準（始まり）の年度としていますので、
求める答えは
\(\,1985\,\)年の\(\,\color{red}{38}\,\)年後
\(\,1985+38=2023\)
となります。
答え \(\color{black}{\fbox{ ウ }}\) \(\,\underline{ 2023 } \,\)
\(\color{black}{\fbox{ 4 }}\)は以上です。
\(\color{black}{\fbox{ 5 }}\) \(\color{black}{\fbox{ 6 }}\)はグラフと図が与えられているので、問題の条件を書き込めればすぐに終わります。
平行四辺形の成立条件と三角形の面積
\(\color{black}{\fbox{ 5 }}\)
「下の図のように」とグラフが書かれていますが、座標はありません。
問題文にある座標を書き込みましょう。
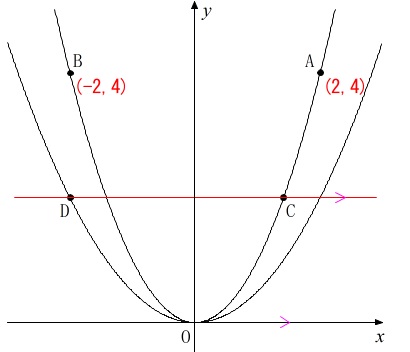
\(\,\mathrm{A\,(\,2\,,\,4\,)\,,\, B\,(\,-2\,,\,4\,)}\,\)
\(\,\mathrm{C}\,\)は\(\,y=x^2\,\)上の点で\(\,0\,＜\,x\,＜\,2\,\)の範囲にある
\(\,\mathrm{C}\,\)を通り\(\,x\,\)軸と平行な直線と\(\displaystyle \,y=\frac{1}{2}x^2\,\)との交点を\(\,\mathrm{D}\,\)
（ただし、\(\,\mathrm{D}\,\)は\(\,x\,\)座標の小さい方）
(1)
四角形\(\,\mathrm{BDCA}\,\)が平行四辺形となるとき、
\(\,\mathrm{BA}\,/\!/\,\mathrm{DC}\,\)なので、
\(\,\mathrm{BA=DC}\,\)
となれば平行四辺形になります。
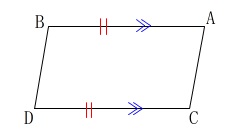四角形が平行四辺形になる条件は5つありますが、
「\color{red}{\(\,1\,\)組の対辺が平行で等しいとき}」
がそのうちの1つですね。
基本編の『覚え太郎』は高校入試では必ず使いますので、完全に覚えておきましょう。
(1)
平行四辺形になる条件から、
\(\,\mathrm{\color{red}{ＡＢ=ＣＤ}}\,\)
となれば良いので、\(\,\mathrm{ＡＢ}\,\)の長さを求めればそれそのまま\(\,\mathrm{ＣＤ}\,\)の長さです。
\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)は\(\,y\,\)座標が同じなので、
「\(\,x\,\)座標の差の絶対値」が長さになりますね。
\(\begin{eqnarray}
ＣＤ&=&ＡＢ\\
&=&2-(-2)\\
&=&\underline{ 4 }
\end{eqnarray}\)
\(\,\mathrm{C}\,\)や\(\,\mathrm{D}\,\)の座標は聞かれていませんので、
この問題では座標を設定する必要がありません。
(2)
\(\,\mathrm{△BDC}\,\)と\(\,\mathrm{△DOC}\,\)の面積が等しくなるときの直線\(\,\mathrm{OD}\,\)の式を求めます。
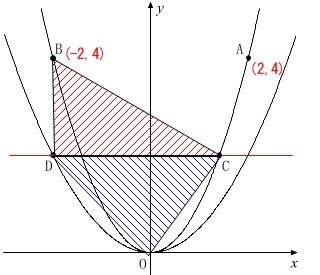\(\,\mathrm{△BDC}\,\)と\(\,\mathrm{△DOC}\,\)は、
\(\,\mathrm{DC}\,\)を共通の底辺
としているので高さが同じなら面積は等しくなります。
高さは\(\,y\,\)座標で見るだけで良いので、
\(\,\mathrm{D}\,\)の\(\,y\,\)座標が、\(\,\mathrm{B}\,\)の\(\,y\,\)座標の半分
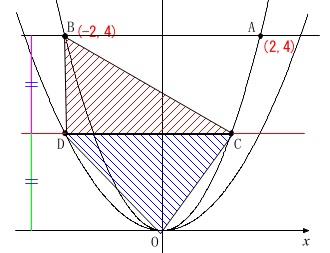
となれば面積は等しくなります。
\(\,\mathrm{B}\,\)の\(\,y\,\)座標が\(\,4\,\)なので、
\(\,\mathrm{D}\,\)の\(\,y\,\)座標は\(\,2\,\)
\(\,\mathrm{D}\,\)は\(\displaystyle \,y=\frac{1}{2}x^2\,\)上の点なので\(\,y=2\,\)を代入して
\(\begin{eqnarray}\displaystyle
2&=&\frac{1}{2}x^2\\
4&=&x^2\\
x&=&\pm 2
\end{eqnarray}\)
\(\,\mathrm{D}\,\)の\(\,x\,\)座標は\(\,y\,\)軸よりも左にあるので、
\(\,x=-2\,\)
このとき\(\,\mathrm{D}\,\)の座標は\(\,(\,-2\,,\,2\,)\,\)となります。
よって、求める\(\,\mathrm{OD}\,\)の式は
\(\,(\,0\,,\,0)\,\)と\(\,(\,-2\,,\,2\,)\,\)
を通る比例です。
\(\,\underline{ y=-x }\,\)
残すは \(\color{black}{\fbox{ 6 }}\) だけです。
円周角と相似
\(\color{black}{\fbox{ 6 }}\)
\(\color{black}{\fbox{ 6 }}\)は円周角と相似の証明です。
\(\,\mathrm{∠AFC=∠CDE}\,\)の証明ですが、相似を証明することと同じです。
広島県の解答では直角三角形を利用した角度によって証明していますが、
垂線\(\,\mathrm{DE}\,\)の条件を与えられた時点で相似が言えるので、どちらでも良いです。
条件をまとめておきます。
条件
線分\(\,\mathrm{BC}\,\)は半円の直径
\(\,\mathrm{\stackrel{\frown}{\mbox{AD}}=\stackrel{\frown}{\mbox{DB}}}\,\)
\(\,\mathrm{DE}\,\) ⊥ \(\,\mathrm{BC}\,\)
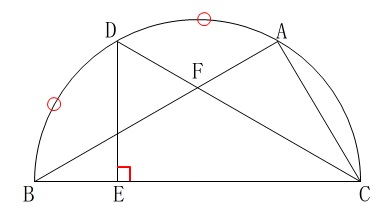これらから次のことが言えます。
\(\,\mathrm{∠BAC=90^{\circ}}\,\)
\(\,\mathrm{∠ACD=∠DCB}\,\)
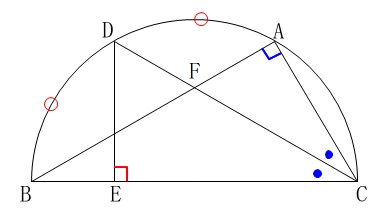それでは理由をつけて証明しておきます。
（証明）
\(\,\mathrm{△AFC}\,\)と\(\,\mathrm{△EDC}\,\)において、
直径\(\,\mathrm{BC}\,\)に対する円周角は\(\,90^{\circ}\,\)なので、
\(\,\mathrm{∠FAC=90^{\circ}}\, ･･･①\)
また仮定から
\(\,\mathrm{∠DEC=90^{\circ}}\, ･･･②\)
①②から
\(\,\mathrm{\color{red}{∠FAC=∠DEC}}\, ･･･③\)
また、\(\,\mathrm{\stackrel{\frown}{\mbox{AD}}=\stackrel{\frown}{\mbox{DB}}}\,\)であることから、
同一長（等しい）の弧に対する円周角は等しくなるので、
年も年も\(\,\mathrm{\color{red}{∠ACF=∠ECD}}\, ･･･④\)
③④より\(\,2\,\)組の角がそれぞれ等しいので
\(\,\mathrm{△AFC}\,\) ∽ \(\,\mathrm{△EDC}\,\)
相似な図形の対応する角は等しいので、
\(\,\mathrm{∠AFC=∠EDC}\,\)
すなわち
\(\,\mathrm{∠AFC=∠CDE}\,\)
（終わり）
「等しい」という場合は「長さが等しい」という意味になります。
この証明の様に相似を利用する場合は記号の順番には気をつけてください。
結論は相似な図形の記号順にはなっていません。
角度が等しいことだけを利用した場合は記号の順番は気にしなくて大丈夫です。
\(\,2018\,\)年の広島県公立高校入試、数学の問題は以上です。
試験時間は\(\,50\,\)分ありますので十分見直しする時間があります。
前半に配点が大きくなっているので見直しをしっかりやって高得点を獲得しましょう。
\(\,2019\,\)年も傾向は同じです。
傾向をつかんだら基本問題を全国の過去問で復習しておくといいですよ。
似たような問題は毎年あちこちの都道府県で見かけます。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
