三重県公立高校入試(2018年)前期選抜試験数学の問題と解説

2018年(平成30年度)に三重県で行われた公立高校入試前期選抜試験数学の問題と解説です。
前期選抜ではすべての公立高校で数学が学科試験にあるわけではなく、
ある程度の数学の力はあると見なされる受験生が受けることになるので、ほんの少し程度をあげて解説しておきます。

問題は三重県で公表してくれています。

⇒　2018年三重県前期選抜数学問題

後期試験よりは少し問題が難しめにはなりますが、
余り複雑に考えず、シンプルに見るとそれほど難しさは感じない問題です。

満点を狙わないのであれば、分かる問題を計算ミスがないように確実にとっていくと良いです。
\(\,50\,\)点満点中\(\color{black}{\fbox{　1　}}\)だけで\(\,18\,\)点(\(\,36\,\)％)ありますからね。

会員対象の解説になりますので少し省略する所がありますがご了承下さい。

式の計算や方程式および円周角と作図

　\(\color{blue}{\fbox{　1　}}\)
(1)
計算順序の確認です。

　\(\hspace{10pt}-9-2\times 4\\
=-9-8\\
=\underline{　-17　}\)

かけ算割り算部分が先ですね。

(2)
割り算は逆数のかけ算です。

　\(\hspace{10pt}\displaystyle (6xy-27y^2)\div \left(-\frac{3}{4}\color{red}{y}\right)\\
\displaystyle =(6xy-27y^2)\times \left(-\frac{4}{\,3\color{red}{y}\,}\right)\\
\displaystyle =6xy\times \left(-\frac{4}{\,3y\,}\right)-27y^2\times\left(-\frac{4}{\,3y\,}\right)\\
\displaystyle =\underline{　-8x+36y　}\)

赤字の\(\,\color{red}{y}\,\)は分子にあるので逆数にすると分母にまわります。

(3)
与式を簡単にしてから最後に代入しましょう。

　\(\hspace{10pt}5(x+2y)-4(2x+3y)\\
=5x+10y-8x-12y\\
=-3x-2y\\
=-3\times (\color{red}{3})-2\times (\color{blue}{-7})\\
=-9+14\\
=\underline{　5　}\)

代入するときは正の数でも負の数でも（かっこ）をつけるようにしておくと計算ミスは減りますよ。

(4)
変化の割合、傾きの関係式です。
\(\,1\,\)次関数では変化の割合と傾きが一致します。

　\(\displaystyle (変化の割合)=\frac{　(\color{red}{\,y\,の増加量})　}{　(\color{blue}{\,x\,の増加量})　}\)

です。
与えられた\(\,1\,\)次関数の傾き(変化の割合)が\(\,\displaystyle \color{magenta}{\frac{3}{2}}\,\)なので、
\(\,x\,\)の増加量が\(\,\color{blue}{5}\,\)のとき、

　\(\begin{eqnarray}
\displaystyle \frac{　(\,\color{red}{\,y\,の増加量)　}\,}{　\color{blue}{5}　}&=&\color{magenta}{\frac{3}{2}}\\
(\color{red}{\,y\,の増加量})&=&\color{magenta}{\frac{3}{2}}\times \color{blue}{5}\\
&=&\underline{　\frac{15}{2}　}
\end{eqnarray}\)

(5)
無理数の有理化と分数の引き算です。

　\(\hspace{10pt}\displaystyle \sqrt{\frac{8}{3}}-\frac{\sqrt{54}}{4}\\
\displaystyle =\frac{2\sqrt{2}}{\sqrt{3}}-\frac{3\sqrt{6}}{4}\\
\displaystyle =\frac{2\sqrt{6}}{3}-\frac{3\sqrt{6}}{4}\\
\displaystyle =\frac{2\sqrt{6}\times 4-3\sqrt{6}\times 3}{12}\\
\displaystyle =\frac{8\sqrt{6}-9\sqrt{6}}{12}\\
\displaystyle =\underline{　\frac{-\sqrt{6}}{12}　}\)

通分は分母を1つにすると分子の計算に集中できます。

答えの\(\displaystyle \,\frac{-\sqrt{6}}{12}\,\)は\(\displaystyle \,-\frac{\sqrt{6}}{12}\,\)でも良いですが、
マイナス(-)は分母にはおかないようにしましょう。

(6)
2次方程式を解くときの基本操作はすべての項を左辺に集めて、
　\(\,(左辺)=0\,\)
にすることです。

　\(\begin{eqnarray}
(2x-1)^2&=&3(x-1)(x+2)+25\\
4x^2-4x+1&=&3(x^2+x-2)+25\\
4x^2-4x+1&=&3x^2+3x-6+25\\
x^2-7x-18&=&0\\
(x+2)(x-9)&=&0\\
x&=&\underline{　-2\,,\,9　}
\end{eqnarray}\)

展開は丁寧にしないとミスしますよ。

(7)
文字式を使える様になることは数学の基本中の基本です。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

十の位の数を\(\,x\,\)とすると、
一の位が\(\,4\,\)なので、
　\(\,\mathrm{A}=10x+4\,\)

各位の数の和が\(\,x+4\,\)で、この\(\,7\,\)倍が\(\,\mathrm{A}\,\)に等しいので、

　\(\begin{eqnarray}
10x+4&=&7(x+4)\\
10x+4&=&7x+28\\
3x&=&24\\
x&=&\color{red}{8}
\end{eqnarray}\)

これが答えではありません。
答えは

　\(\begin{eqnarray}
\mathrm{A}&=&10\times \color{red}{8}+4\\
&=&\underline{　84　}\,\end{eqnarray}\)

問題が聞いている答えは確認しておきましょう。

(8)
条件がありすぎて方針で迷うくらいですが、
素直に円周角の等しい所を見ていけば簡単です。

条件
　\(\,\mathrm{∠BAC=58^{\circ}}\,\)
　\(\,\mathrm{\stackrel{\frown}{\mbox{AD}}=\stackrel{\frown}{\mbox{DB}}}\,\)
　\(\,\mathrm{\stackrel{\frown}{\mbox{CE}}=\stackrel{\frown}{\mbox{EA}}}\,\)

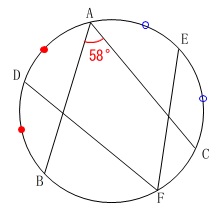
中心が与えられているので中心角にが目が行ってしまいますが、
円に内接している四角形の対角の和が\(\,180^{\circ}\,\)であることを利用すれば必要ありません。

前期試験で数学を課す高校を受験するレベルにある人向けの解説なので、
知っているとして説明していますが、知らない人は『覚え太郎』やった方が良いです。
学校でもやっているとは思うのですが、、、
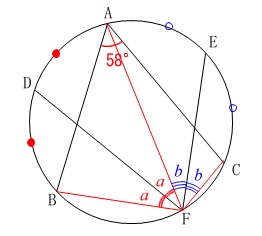四角形\(\,\mathrm{ABFC}\,\)は円に内接しているので、

　\(\mathrm{∠BAC+∠BFC}=180^{\circ}\)
なので
　\(58^{\circ}+2(\color{red}{a}+\color{blue}{b})=180^{\circ}\)

このことから、\(\,\color{red}{a},\color{blue}{b}\,\)は具体的には求まりませんが\(\,\color{red}{a}+\color{blue}{b}\,\)は求まります。

　\(\begin{eqnarray}
58^{\circ}+2(\color{red}{a}+\color{blue}{b})&=&180^{\circ}\\
2(\color{red}{a}+\color{blue}{b})&=&(180-58)^{\circ}\\
&=&122^{\circ}\\
\color{red}{a}+\color{blue}{b}&=&61^{\circ}
\end{eqnarray}\)

よって

　\(\begin{eqnarray}
\mathrm{∠DFE}&=&\color{red}{a}+\color{blue}{b}\\
&=&\underline{　61^{\circ}　}
\end{eqnarray}\)

中心角を利用する方法は自分でチャレンジしてみて下さい。
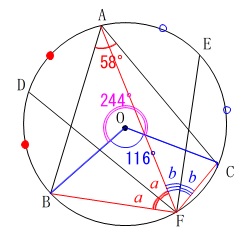中心角が出れば、自然と答えは出てくるでしょう。

いずれにしても、ぼーと問題を見ているだけでは答えは出ません。
手を動かして、少しくらいは『作業』しましょう。
　
(9)
作図問題です。
\(\,\mathrm{BC}\,\)が共通の底辺で三角形の面積を半分にするので、
高さが半分になれば良いということです。

パッと見て、2つ考えられるのではないでしょうか。

1つは中点連結定理を利用して、\(\,\mathrm{AB}\,\)と\(\,\mathrm{AC}\,\)の中点を結んで高さを半分にする。

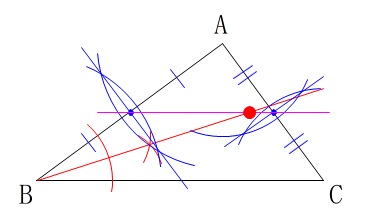
もう一つは、\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)に垂線を引いて、その垂直二等分線を引く。
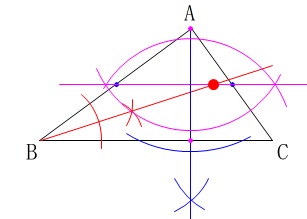後は\(\,\mathrm{△DBC}\,\)となるように辺\(\,\mathrm{DC}\,\)を引くだけです。

どちらも\(\,\mathrm{BC}\,\)を底辺として、高さが半分になるので、
　\(\displaystyle \mathrm{△DBC}=\frac{1}{2}\mathrm{△ABC}\)
を満たしています。
　
\(\color{black}{\fbox{　1　}}\)は以上ですが全体の\(\,36\,\)％ありますので、
配点が\(\,18\,\)点ではなく、配点が\(\,36\,\)％あるということを知っておきましょう。
実は大きい配点なのです。

無理数の性質と相対度数分布表の見方

　\(\color{blue}{\fbox{　2　}}\)

(1)
無理数の値と文字式の計算です。

①
\(\,2\sqrt{7}-3\,\)の整数部分を求めますが、
　\(\sqrt{4}\,＜\,\sqrt{7}\,＜\,\sqrt{9}\)
なので
　\(2\,＜\,\sqrt{7}\,＜\,3\)
とするのは範囲を大きく分けすぎです。

すべての辺を\(\,2\,\)倍すると
　\(4\,＜\,2\sqrt{7}\,＜\,6\)
となるので、\(\,\,2\sqrt{7}\,\,\)の整数部分が\(\,4,5\,\)のどちらか分かりません。

そこで判断するには\(\,\sqrt{7}\,\)が\(\,2.5\,\)を超えるのか超えないのかで、
\(\,2\sqrt{7}\,\)の整数部分が\(\,4\,\)か\(\,5\,\)の違いが分かります。

　\(2.5^2=6.25\,\)なので\(\,2.5^2\,＜\,7＜3^2\,\)

正の平方根で考えて良いので
　\(2.5\,＜\,\sqrt{7}\,＜\,3\)
ここで\(\,2\,\)倍すると
　\(5\,＜\,2\sqrt{7}\,＜\,6\)
このことから全部の辺から\(\,3\,\)を引いて
　\(2\,＜\,2\sqrt{7}-3\,＜\,3\)

よって、
　\(\,2\sqrt{7}-3\,\)の整数部分は\(\,\underline{　2　}\,\)

②
　\(\,無理数=\color{blue}{整数部分}+\color{red}{小数部分}\,\)

①で整数部分は分かったので小数部分\(\,\color{red}{a}\,\)は、
全体から整数部分\(\,\color{blue}{2}\,\)を引けば良いです。

　\(\begin{eqnarray}
a&=&(2\sqrt{7}-3)-\color{blue}{2}\\
&=&\color{red}{2\sqrt{7}-5}
\end{eqnarray}\)

後の計算は代入するだけで良いです。
ちょっと工夫すれば楽にはなりますが、この程度の計算なら力業でも良いでしょう。笑

　\(\begin{eqnarray}
a^2+5a&=&(\color{red}{2\sqrt{7}-5})^2+5(\color{red}{2\sqrt{7}-5})\\
&=&28-20\sqrt{7}+25+10\sqrt{7}-25\\
&=&28-10\sqrt{7}
\end{eqnarray}\)

与式（求値式）を因数分解してみると

　\(a^2+5a=a(a+5)\)
となります。
　\(\begin{eqnarray}
a&=&2\sqrt{7}\color{blue}{-5}\\
a\color{blue}{+5}&=&2\sqrt{7}
\end{eqnarray}\)
なので、
　\(\begin{eqnarray}
a^2+5a&=&a(a+5)\\
&=&(2\sqrt{7}-5)\times 2\sqrt{7}\\
&=&\underline{　28-10\sqrt{7}　}
\end{eqnarray}\)

文字式の代入計算問題は楽になる方法が隠されている場合が多いです。
ただ、この問題は、
両辺平方して無理数部分を消す処理をするのが普通になっている『覚え太郎』会員には、
逆に簡単すぎました。笑

(2)
相対度数分布表と度数折れ線（度数分布多角形）の読み取り問題です。
が、度数折れ線は必要無いのでは？と思える問題です。

簡単なので先に表の空白部分を埋めておきます。

\(\color{black}{\fbox{(あ)}}\)は度数ですが、
　\(\,40\,\)人に対する相対度数が\(\,0.25\,\)
なので
　\(\,\color{black}{\fbox{(あ)}}=40\times 0.25=\underline{　10　}\,\)

これにより度数合計が\(\,40\,\)であることから\(\color{black}{\fbox{(い)}}\)が分かります。

　\(\begin{eqnarray}
\color{black}{\fbox{(い)}}&=&40-(2+10+8+2)\\
&=&40-22\\
&=&\underline{　18　}
\end{eqnarray}\)

このことから相対度数\(\color{black}{\fbox{(う)}}\)は

　\(\color{black}{\fbox{(う)}}=18\div 40=\underline{　0.45　}\)

表の空白を埋めて完成させておきます。
（表から度数折れ線は描かれるのでこれを読み取れば図は必要ありません。）
\(\,\mathrm{A}\,\)中学校でも\(\,\mathrm{A}\,\)高校でも同じなので「中学校」を省略します。

　\(\begin{array}{|c|c|c|c|c|} \hline
\,階級\, & \,\mathrm{A}\,&\,\mathrm{A}\,&\,\mathrm{B}\,&\,\mathrm{B}\,\\
\,(時間)\, & \,度数\,&\,相対度数\,&\,度数\,&\,相対度数\, \\ \hline
\,0～5\, & 0 & 0.00 & 0 & 0.00\\
\,5～6\, & 2 & 0.05 & 8 & 0.05 \\
\,6～7\, & 10 & 0.25 & 36 & 0.23 \\
\,7～8\, & \color{magenta}{18} & 0.45 & \color{blue}{47} & 0.29 \\
\,8～9\, & 8 & 0.20 & \color{red}{59} & 0.37 \\
\,9～10\, & 2 & 0.05 & 10 & 0.06 \\
\,10～　 & 0 & 0.00 & 0 & 0.00 \\\hline
\,計\, & 40 & 1.00 & 160 & 1.00 \\\hline
\end{array}\)

②
ア．中央値についてです。

\(\,\mathrm{A}\,\)の中央値は累積度数\(\,20\,\)か\(\,21\,\)になる人の値なので度数\(\,\color{magenta}{18}\,\)の
　\(\,7\,\)時間以上\(\,8\,\)時間未満の階級の階級値
\(\,\mathrm{B}\,\)は累積度数が\(\,80\,\)か\(\,81\,\)になる人の値なので度数\(\,\color{blue}{47}\,\)の
　\(\,7\,\)時間以上\(\,8\,\)時間未満の階級の階級値
で同じになります。　

イ．最頻値は簡単で、
　\(\,\mathrm{A}\,\)の最頻値は度数\(\,\color{magenta}{18}\,\)の階級の階級値
　\(\,\mathrm{B}\,\)の最頻値は度数\(\,\color{red}{59}\,\)の階級の階級値
で異なります。

ウ．\(\,\mathrm{B}\,\)の睡眠時間が\(\,8\,\)時間以上の生徒数は、
　\(\,59+10=69\,\)
これは半数に届いていません。
\(\,8\,\)時間以上の相対度数合計で見ればすぐに分かります。
　\(0.37+0.06=0.43\)
これは半分\(\,(0.5)\,\)以下であることを意味しています。

エ．睡眠時間が\(\,8\,\)時間未満の生徒の相対度数合計は、
　\(\,\mathrm{A}\,\):　\(\,0.05+0.25+0.45=0.75\,\)
　\(\,\mathrm{B}\,\):　\(\,0.05+0.23+0.29=0.57\,\)
となっているので、\(\,\mathrm{A}\,\)の方が大きい。

エ．は睡眠時間\(\,8\,\)時間以上の生徒の相対度数合計を出して、少ない方が\(\,8\,\)時間未満の相対度数合計が大きい、と見ても良いですよ。

ところで、\(\,\mathrm{B}\,\)の相対度数1つひとつは四捨五入してあります。
その場合、相対度数合計がちょうど\(\,1.00\,\)にならない場合がありますが、その場合は度数の一番大きい階級の数値で調整するのですよ。
忘れている人は『覚え太郎』の基本レポートを読み直しておいて下さい。
この問題では四捨五入した数値で相対度数合計が\(\,1.00\,\)になっているので考えなくて良いです。

\(\color{black}{\fbox{　2　}}\)は以上です。

ここで思い出しました。
簡単に解説するはずが長くなっています。笑
詳しい解説は後期試験でしますので、後は簡単に済ませます。

図形の移動と重なる面積の関係とグラフ

　\(\color{blue}{\fbox{　3　}}\)

図形が移動して重なる面積を考える問題です。
申し訳無いですが、問題にある条件は自分で抜き出して図は自分で書いてから考えて下さい。
\(\,\mathrm{\color{red}{∠ABC=45^{\circ}}}\,\)であることは見抜いておいて下さい。

(1)
\(\,x=1\,\)のとき、つまり長方形が右に\(\,\mathrm{1\,cm}\,\)動いたときの重なる三角形の面積\(\,y\,\)です。
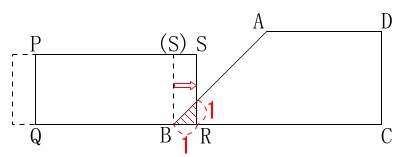　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 1\times 1\\
&=&\underline{　\frac{1}{2}　}
\end{eqnarray}\)

(2)
\(\,0\,≦\,x\,≦\,3\,\)の範囲では、
重なる部分はまだ三角形のままであることは分かりますよね。
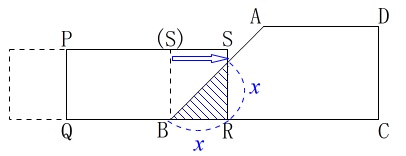　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times x\times x\\
&=&\underline{　\frac{1}{2}\,x^2　}　（0≦x≦3)
\end{eqnarray}\)

(3)
\(\,x=3\,\)のときが1つの境目になります。
\(\,3\,\)秒後には\(\,\mathrm{S}\,\)は\(\,\mathrm{AB}\,\)上にあるので、
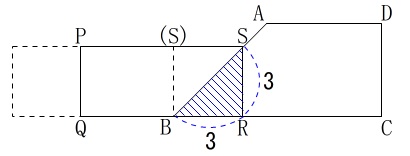その後は増える重なり部分は長方形になります。

長方形部分の縦(高さ)は\(\,\mathrm{3\,cm}\,\)で一定ですが横の長さは、
移動した\(\,x\,\)秒から\(\,\mathrm{AB}\,\)と重なるまでの\(\,3\,\)秒分を引いた\(\,\color{magenta}{x-3}\,\)です。
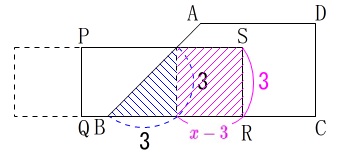よって重なり部分の面積は、

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 3\times 3+\color{magenta}{3}(\color{magenta}{x-3})\\
&=&\frac{9}{2}+3x-9\\
&=&\underline{　3x-\frac{9}{2}　}　(3≦x≦7)
\end{eqnarray}\)

(4)
(2)と(3)で求めた放物線と直線のグラフをつなげるだけです。
　\(\displaystyle \left(\,3\,,\,\frac{9}{2}\,\right)\)　\(\displaystyle \left(\,7\,,\,\frac{33}{2}\,\right)\)
を通ることだけ注意しておけば答えはすぐに見つかります。

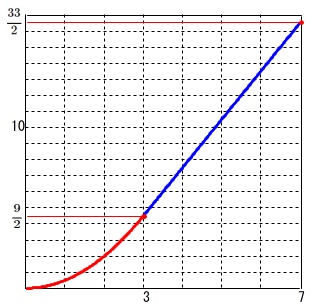
　答えは　\(\,\underline{　イ　}\,\)

(5)
重なる部分の面積と長方形\(\,\mathrm{ABCD}\,\)の面積比が\(\,1：4\,\)になる\(\,x\,\)を求めます。

四角形\(\,\mathrm{ABCD}\,\)は台形なので面積は、
　\(\begin{eqnarray}
　(四角形\mathrm{ABCD})&=&\frac{1}{2}\times (5+9)\times 4\\
&=&28
\end{eqnarray}\)

だから重なる部分の面積が\(\,7\,\)となる\(\,x\,\)を求めれば良いのです。
グラフを見てもわかりますが、
\(\,y=7\,\)となるのは\(\,4≦x≦7\,\)の範囲になるので、
\(\displaystyle \,y=3x-\frac{9}{2}\,\)に\(\,y=7\,\)を代入します。

　\(\begin{eqnarray}\displaystyle
7&=&3x-\frac{9}{2}\\
14&=&6x-9\\
-6x&=&-9-14\\
6x&=&23\\
x&=&\underline{　\frac{23}{6}　}
\end{eqnarray}\)

(2)(3)で関数を求めているので利用しましょう。
問題は親切に導いてくれているのですよ。

\(\color{black}{\fbox{　3　}}\)は以上です。
ここはサクッと\(\,5\,\)分くらいで終わらせておきたい所ですね。

立体の相似と確率のルール確認

　\(\color{blue}{\fbox{　4　}}\)

正四角錐の体積比問題と確率です。
どちらも単純に考えればすぐに終わります。

(1)
\(\,\mathrm{E,F,G,H}\,\)はそれぞれ\(\,\mathrm{OA,OB,OC,OD}\,\)の中点なので、

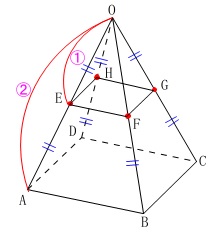
四角錐\(\,\mathrm{OEFGH}\,\)も正四角錐で、
四角錐\(\,\mathrm{OABCD}\,\)と四角錐\(\,\mathrm{OEFGH}\,\)は相似です。

相似比が\(\,2:1\,\)なので
体積比は\(\,2^3:1^3=8:1\,\)だから

　\(\,\mathrm{OEFGH}\,\)の体積は\(\,\mathrm{OABCD}\,\)の\(\displaystyle \,\frac{1}{8}\,\)

だから、

立体\(\,\mathrm{K}\,\)（錐台）の体積は正四角錐\(\,\mathrm{OABCD}\,\)の

　\(\hspace{10pt} \displaystyle 1-\frac{1}{8}=\underline{　\frac{7}{8}　倍}\)

(2)
\(\,5\,\)枚のカードをルールに従って裏返します。

【ルール】を簡単に言うと、

さいころを投げて、
　\(\,1,2,3,4,5\,\)が出目のときはその番号のカードを裏返す。
　\(\,6\,\)の目が出たときはすべてのカードを裏返す。

①
さいころを\(\,1\,\)回投げ、番号\(\,3\,\)の下にあるカードが黒になる確率です。

元が白なので、裏返る必要があります。

よって、
　さいころの出目が\(\,3\,\)で[\(\,3\,\)]のカードだけが裏返るか、
　さいころの出目が\(\,6\,\)ですべてのカードが裏返るか
のどちらかなので、
　\(\displaystyle \frac{2}{6}=\underline{　\frac{1}{3}　}\)

②
さいころを\(\,2\,\)回投げます。

さいころ\(\,2\,\)回投げた後、
　黒のカードが白のカードより多い確率
　（黒が\(\,3\,\)枚以上になっている確率）
を求めます。

さいころを\(\,2\,\)回投げるので\(\,36\,\)通りの場合があります。
樹形図か表を書けば良いだけですが、すべてを書き出す必要もないでしょう。

\(\,1\,\)回目\(\,1\,\)の目が出たとき、[\(\,1\,\)]のカードは裏返って黒になっているので、
全部で黒は\(\,3\,\)枚になっています。
　\(\begin{array}{|c|c|c|c|c|} \hline
　[\,1\,]　&　[\,2\,]　&　[\,3\,]　&　[\,4\,]　&　[\,5\,]　 \\ \hline
　●　&　●　&　○　&　●　&　○　\\ \hline
\end{array}\)

このとき黒の方が多いので、\(\,2\,\)回目のさいころで
　黒が裏返る\(\,1,2,4\,\)の目が出ると白の方が多くなる
　\(\,6\,\)の目が出てすべてが裏返れば白の方が多くなる
のでダメです。

つまり、
　白で残っている\(\,3,5\,\)が\(\,2\,\)回目の出目
なら黒が\(\,4\,\)つになり黒が多くなります。

\(\,1\,\)回目\(\,2\,\)が出ると白が\(\,4\,\)枚になっているので、
　\(\begin{array}{|c|c|c|c|c|} \hline
　[\,1\,]　&　[\,2\,]　&　[\,3\,]　&　[\,4\,]　&　[\,5\,]　 \\ \hline
　○　&　○　&　○　&　●　&　○　\\ \hline
\end{array}\)
\(\,2\,\)回目\(\,6\,\)の目が出てすべてが裏返るしか黒が多くなる場合はありません。

このように考えると、\(\,1\,\)回目の出目と\(\,2\,\)回目の出目の組み合わせで黒が多くなるのは、
\(\,1\,\)回目に\(\,6\,\)が出て、白黒が逆になっている場合も考えて、

　\(\begin{array}{|c|c|c|} \hline
　1回目　&　2回目　&　黒の枚数　\\ \hline
　1　&　3　&　4　\\ \hline
　1　&　5　&　4　\\ \hline
　2　&　6　&　4　\\ \hline
　3　&　1　&　4　\\ \hline
　3　&　5　&　4　\\ \hline
　4　&　6　&　4　\\ \hline
　5　&　1　&　4　\\ \hline
　5　&　3　&　4　\\ \hline
　6　&　2　&　4　\\ \hline
　6　&　4　&　4　\\ \hline
\end{array}\)

の\(\,10\,\)通りだけです。

よって求める確率は、
　\(\displaystyle \frac{10}{36}=\underline{　\frac{5}{18}　}\)

\(\,36\,\)通りすべての表（または樹形図）を書けばややこしいことを考えることなく答えは出ますよ。

(2)は①②ともに、
書く気があるかないかだけで決まる\(\,4\,\)点です。
（\(\,100\,\)点満点で見れば\(\,8\,\)点分）

これで\(\color{black}{\fbox{　4　}}\)は終わりです。

合同と相似と面積比

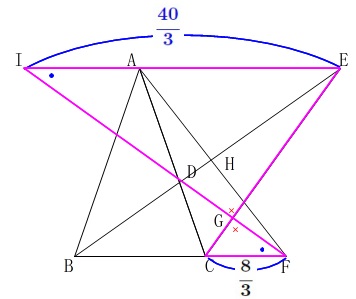
　\(\color{blue}{\fbox{　5　}}\)

「次の図のように」という、めんどくさ、、、っと、
ややこしそうな日本語で書かれた条件が\(\,4\,\)行にわたって書いてあります。

条件を抜き出しておきます。

　\(\,\mathrm{AB=AC}\,\)
　\(\,\mathrm{BE}\,\)は\(\,\mathrm{∠ABC}\,\)の二等分線
　\(\,\mathrm{BD=DF}\,\)

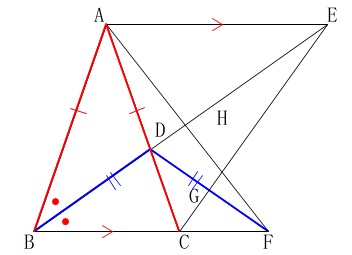
後は条件通りの交点です。

この与えられた条件から言えることは山ほどありますが、
できるだけ図に書き出しておくことです。

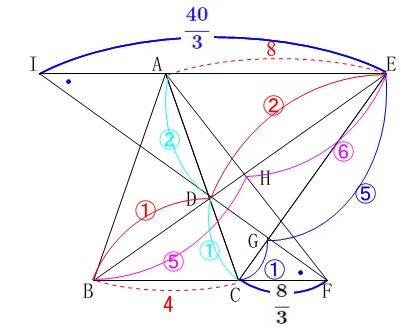
(1)
合同の証明ですが、証明は図の中で終わらせておくことがポイントです。
図の中で示せないことが文章で示せる訳がありません。
分かることを順に書き込んで見ました。
分かり易くするために角度も記号を用いて表していますので、少しだけ説明をしておきます。

\(\,\mathrm{∠ABE}=\color{red}{a}\,\)
\(\,\mathrm{∠AEC}=\color{blue}{b}\,\)
とおいておきます。

\(\,\mathrm{△ABC}\,\)は二等辺三角形なので、
　\(\,\mathrm{∠ABC}=\mathrm{∠ABC}=\color{red}{2a}\,\)

\(\,\mathrm{△DBF}\,\)も二等辺三角形なので、
　\(\,\mathrm{∠DBC}=\mathrm{∠DFB}=\color{red}{a}\,\)

\(\,\mathrm{△ACE}\,\)も二等辺三角形なので、
　\(\,\mathrm{∠ACE}=\mathrm{∠AEC}=\color{blue}{b}\,\)

\(\,\mathrm{AE}\, /\!/ \,\mathrm{BF}\,\)なので錯角が等しいことから、
　\(\,\mathrm{∠AEC}=\mathrm{∠FCE}=\color{blue}{b}\,\)

また、
\(\,\mathrm{△CDF}\,\)において外角\(\,\mathrm{∠BCD}=\color{red}{2a}\,\)なので、
\(\,\mathrm{∠CDF+∠CFD}=\color{red}{2a}\,\)だから
　\(\,\mathrm{∠CDF}=\color{red}{a}\,\)

このことから、\(\,\mathrm{△CDF}\,\)も二等辺三角形になるので、
　\(\,\mathrm{CD=CF}\,\)

\(\,\mathrm{CG}\,\)は共通の辺であることから、
　\(\,\mathrm{CG=CG}\,\)

以上のことから　
　\(\,2\,\)組の辺とその間の角がそれぞれ等しい
ので、
　\(\,\mathrm{△CDG}\,\)　≡　\(\,\mathrm{△CFG}\,\)

と合同の証明は終わりです。
文章は適当に自分でまとめておいて下さい。笑

(2)
相似な図形の発見と、辺の長さと線分比および面積比を求める問題です。

難しそうに見えるのですが、この問題こそシンプルにみれば簡単です。

①
\(\,\mathrm{AE}\, /\!/ \,\mathrm{BF}\,\)なので、
　\(\,\mathrm{△DAE}\,\)　∽　\(\,\mathrm{△DCB}\,\)
相似比は
　\(\begin{eqnarray}
\mathrm{AE:BC}&=&8:4\\
&=&\color{blue}{2}:\color{blue}{1}
\end{eqnarray}\)

\(\,\mathrm{△ACE}\,\)は二等辺三角形で\(\,\mathrm{AC=\color{red}{8}}\,\)だから
　\(\begin{eqnarray}\displaystyle
\mathrm{ＣＤ}&=&\frac{\color{blue}{1}}{\color{blue}{2}+\color{blue}{1}}\times \color{red}{8}\\
&=&\frac{8}{3}
\end{eqnarray}\)

\(\,\mathrm{△CDG}\,\)　≡　\(\,\mathrm{△CFG}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{ＣＦ}&=&\mathrm{ＣＤ}\\
&=&\underline{　\frac{8}{3}　}
\end{eqnarray}\)

②
線分\(\,\mathrm{FG}\,\)を延長して相似な三角形を作ります。

　\(\begin{eqnarray}\displaystyle
\mathrm{BF}&=&\mathrm{BC+BF}\\
&=&4+\frac{8}{3}\\
&=&\color{blue}{\frac{20}{3}}
\end{eqnarray}\)
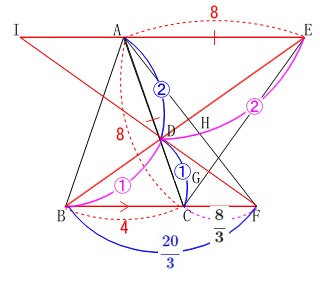　\(\,\mathrm{△DAE}\,\)　∽　\(\,\mathrm{△DCB}\,\)
で相似比が\(\,\color{blue}{2:1}\,\)であったのと同じで、
　\(\,\mathrm{△DIE}\,\)　∽　\(\,\mathrm{△DFB}\,\)
で相似比は同じ\(\,\color{magenta}{2:1}\,\)です。

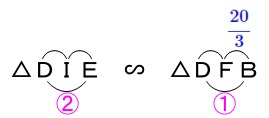
このことから

　\(\begin{eqnarray}
\mathrm{DE:DB}&=&\mathrm{IE:FB}\\
2:1&=&\mathrm{IE}:\frac{20}{3}\\
\mathrm{IE}&=&\color{blue}{\frac{40}{3}}
\end{eqnarray}\)
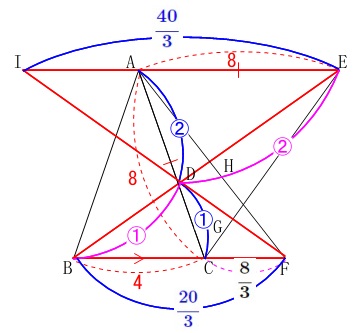ここで相似な三角形を違う形で見ます。
何故か？
求める辺の比が含まれる三角形どうしで見たいからです。

問題は線分\(\,\mathrm{CG}\,\)と線分\(\,\mathrm{GE}\,\)の比なので、
　\(\,\mathrm{\color{magenta}{△CGF}}\,\)　∽　\(\,\mathrm{\color{magenta}{△EGI}}\,\)
を使います。
相似な図形では対応する辺の比は等しいので、

　\(\begin{eqnarray}
\mathrm{CG:EG}&=&\mathrm{CF:EI}\\
&=&\frac{8}{3}:\frac{40}{3}\\
&=&8:40\\
&=&\underline{　1:5　}
\end{eqnarray}\)

③
\(\,\mathrm{△ADH}\,\)と\(\,\mathrm{△CFG}\,\)の面積比を求めます。
方法がいろいろあって迷うかもしれませんが、1つの三角形を基準に比較した方が考えやすいですよ。
実際の面積を出して比較することはできませんので線分比から面積比を求めます。

基準にする三角形を\(\,\mathrm{△ACE}\,\)にするか、\(\,\mathrm{△ACF}\,\)にするかのどちらか、どっちでも良いです。

(1)から
　\(\,\mathrm{△CDB}\,\)　≡　\(\,\mathrm{△CFG}\,\)
を示しているので、
　\(\,\mathrm{△ADH}\,\)と\(\,\mathrm{△CDB}\,\)の面積比
を出せば良いという方向で進めます。

このとき基準にする三角形は\(\,\mathrm{△ACE}\,\)です。
\(\,\mathrm{△AHE}\,\)　∽　\(\,\mathrm{△FHB}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{EH:BH}&=&\mathrm{AE:FB}\\
&=&\color{red}{8}:\color{blue}{\frac{20}{3}}\\
&=&\color{magenta}{6:5}
\end{eqnarray}\)
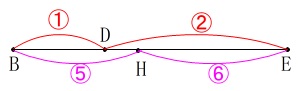
このことから線分\(\,\mathrm{BE}\,\)を抜き出して比を出しておくと、

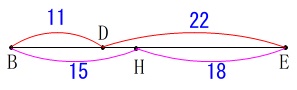
ここで線分\(\,\mathrm{BE}\,\)の長さを、
　\(\,\color{red}{1+2=3}\,\)と\(\,\color{magenta}{5+6=11}\,\)の最小公倍数\(\,\color{blue}{33}\,\)
として比を考えてかまわないので、

　\(\mathrm{BD:DH:HE}=\color{blue}{11:4:18}\)
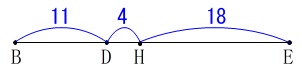ここで\(\,\mathrm{△ACE}\,\)の面積を基準に2つの三角形の面積比を出します。

　\(\begin{eqnarray}
\mathrm{△ADH}&=&\mathrm{△ACE}\times \frac{2}{3}\times \frac{4}{4+18}\\
&=&\mathrm{△ACE} \times \color{red}{\frac{4}{33}}
\end{eqnarray}\)

　\(\begin{eqnarray}
\mathrm{△CFG}&=&\mathrm{△CDG}\\
&=&\mathrm{△ACE}\times \frac{1}{3}\times \frac{1}{1+5}\\
&=&\mathrm{△ACE }\times \color{blue}{\frac{1}{18}}
\end{eqnarray}\)

よって、
　\(\begin{eqnarray} \displaystyle
\mathrm{△ADH:△CFG}&=&\color{red}{\frac{4}{33}}:\color{blue}{\frac{1}{18}}\\
&=&4\times 18:1\times 33\\
&=&\underline{　24:11　}
\end{eqnarray}\)

\(\,\mathrm{△ACF}\,\)を基準にすると、

　\(\begin{eqnarray}\displaystyle
\mathrm{△ADH}&=&\mathrm{△ACF} \times \frac{2}{3}\times \frac{6}{5+6}\\
&=&\mathrm{△ACF}\times \frac{2}{3}\times \frac{6}{11}\\
&=&\mathrm{△ACF}\times \color{red}{\frac{4}{11}}
\end{eqnarray}\)

　\(\begin{eqnarray}
\mathrm{△CFG}&=&\mathrm{△ACF}\times \frac{1}{3}\times \frac{1}{2}\\
&=&\mathrm{△ACF}\times \color{blue}{\frac{1}{6}}
\end{eqnarray}\)

このことから

　\(\begin{eqnarray}\displaystyle
\mathrm{△ADH:△CFG}&=&\color{red}{\frac{4}{11}}:\color{blue}{\frac{1}{6}}\\
&=&4\times 6:1\times 11\\
&=&\underline{　24:11　}
\end{eqnarray}\)

でも良いですね。

いずれにしても線分比を出す問題には十分慣れているでしょうけど、
頭の中で考えていてもなかなか出てきませんよ。

\(\,2018\,\)年度三重県公立入試前期数学はここまでです。

満点を狙いたいなら『超え太郎』と『発展レポート』まで一ケ月程度で仕上げるくらい集中して取り組むと良いです。

⇒　中学数学を短期間で攻略する

後期試験はもう少し基本から詳しく説明した方が良いでしょうね。

⇒　三重県公立高校入試の数学の問題と解説

\(\,2019\,\)年度も前期後期とも解説しておきますので更新を確認して下さい。