三重県公立高校入試2018年度後期試験数学の問題と解説

2018年(平成30年)度に三重県で行われた公立高校入試後期試験の数学の問題と解説です。
前期試験の数学と問題構成は同じですが、数学が苦手な人は配点に気をつけて目標得点に合わせて解ける問題を解いていくと良いです。
後期試験も前半は基本中心の問題が並んでいて配点も大きいので確実に解いておきましょう。

問題は三重県で公開してくれています。

⇒　2018年三重県公立高校入試後期選抜試験の数学問題

式の計算と方程式と度数分布表

　\(\color{blue}{\fbox{　1　}}\)

\(\color{black}{\fbox{　1　}}\)は小問が\(\,7\,\)問ありますが基本ばかりです。

(1)
正負の計算は数直線で考えれば確実です。

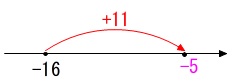
　\(\hspace{10pt}-16+11\\
=\underline{　-5　}\)

マイナスは数直線で左に、プラスは右に動きます。

(2)
割り算は逆数のかけ算です。
この問題は符号に気をつけておけば暗算でできる程度ですが、
基本通りやっておくと計算がややこしくなっても同じです。

　\(\hspace{10pt}\displaystyle -12x \div (-3)\\
\displaystyle =-12x\times \left(-\frac{1}{3}\right)\\
\displaystyle =12x\times \frac{1}{3}\\
=\underline{　4x　}\)

負の数はかける数（割る数）が偶数のときは\(\,+\,\)（プラス）になるの\(\,2\,\)行目はなくても良いですよ。

(3)
分数の通分計算は分母を1つにして分子の計算に集中すると計算ミスは減ります。

　\(\hspace{10pt}\displaystyle \frac{x+y}{2}-\frac{3x-5y}{8}\\
\displaystyle =\frac{4(x+y)-(3x-5y)}{8}\\
\displaystyle =\frac{4x+4y-3x+5y}{8}\\
\displaystyle =\underline{　\frac{x+9y}{8}　}\)

分子には（かっこ）が付いていることは忘れないようにしましょう。

(4)
無理数計算ですがていねいに展開すれば良いだけです。

　\(\hspace{10pt}(\sqrt{3}-2\sqrt{5})^2\\
=(\sqrt{3})^2-2\times \sqrt{3}\times (2\sqrt{5})+(2\sqrt{5})^2\\
=3-4\sqrt{15}+20\\
=\underline{　23-4\sqrt{5}　}\)

展開公式通りの計算なので、

　\(\hspace{10pt}(\sqrt{3}-2\sqrt{5})^2\\
=3-4\sqrt{15}+20\\
=\underline{　23-4\sqrt{15}　}\)

でも良いですが、\(\,2\,\)行目を飛ばすのは入試としてはちょっと暗算しすぎです。
計算ミスしやすくなるだえではなくて、逆に遅くなりますよ。

(5)
因数分解の手順は決まっています。

先ずは共通因数を抜き出しましょう。

　\(\hspace{10pt}6x^2-24\\
=6(\color{red}{x^2-4})\\
=\underline{　6(x+2)(x-2)　}\)

共通因数を抜き出した後、（かっこ）の中が因数分解できないか確認は必ずしましょう。

(6)
\(\,2\,\)次方程式を解くときは因数分解が利用できないかを先に確認した方が良いですが、

⇒　２次方程式を解の公式で解く問題の見分け方と例題

この\(\,2\,\)次方程式
　\(3x^2-x-1=0\)
の左辺は因数分解できません。

なので解の公式です。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-1)\pm \sqrt{(-1)^2-4(3)(-1)}}{2\times 3}\\
&=&\frac{1\pm \sqrt{1+12}}{6}\\
&=&\underline{　\frac{1\pm \sqrt{13}}{6}　}
\end{eqnarray}\)

(7)
度数分布表の最頻値と相対度数を求めます。

代表値の意味さえ分かっていればなんの問題もありません。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

今後は累積度数や累積相対度数を求めよ、という問題が増えてくるでしょう。

①
度数分布表での最頻値は、
　度数が一番多い階級の階級値
となります。

度数が一番多い階級は
　\(\,20\,\mathrm{m}\,\)以上\(\,25\,\mathrm{m}\,\)未満の階級
なのでその階級値は、
　\(\,\underline{　22.5　}\,\)

②
相対度数は度数計\(\,\color{red}{40}\,\)に対する割合です。

\(\,10\,\mathrm{m}\,\)以上\(\,15\,\mathrm{m}\,\)未満の階級の度数は\(\,\color{blue}{8}\,\)だから

　\(\hspace{10pt}\displaystyle \frac{\color{blue}{8}}{\color{red}{40}}=\underline{　0.2　}\)

\(\color{black}{\fbox{　1　}}\)はここまででです。

規則性の文字式と連立方程式の文章題と確率

　\(\color{blue}{\fbox{　2　}}\)

日本語の説明が長いですがここも基本問題が並んでいます。

(1)
正方形がどのように並んでいるか自分で書いて行けば規則性は見えてきます。
考え方は1つではありませんので自分気がついた規則性にしたがって文字式を立てれば良いですよ。
例えば、
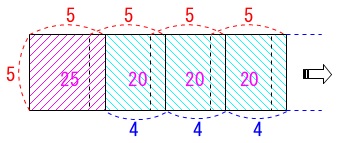最初の\(\,1\,\)辺が\(\,5\,\)の正方形に横の長さが\(\,4\,\)の長方形を\(\,n-1\,\)個加えた、
と見た場合、
　\(\hspace{10pt}25+20(n-1)\\
=25+20n-20\\
=\underline{　20n+5　}　(\mathrm{cm^2})\)

他にも、
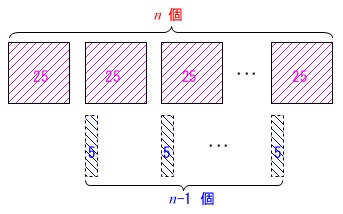面積\(\,\color{magenta}{25}\,\)の正方形が\(\,\color{red}{n}\,\)個あって、
重なり部分の\(\,\color{blue}{5}\,\)が\(\,n-1\,\)個あるのでその分面積が減るので、

　\(\hspace{10pt}25n-5(n-1)\\
=25n-5n+5\\
=\underline{　20n+5　}　(\mathrm{cm^2})\)

と考えた人もいるでしょう。どちらでも良いですよ。
他にも、縦の長さは\(\,\color{red}{5}\,\)で固定だから横の長さを文字式で表して、後で面積にする、でも良いです。

数学の解法は1つではありませんので、あなたの考え方が違っているとは限りません。
数学は厳密であるべきですが、『これじゃないとダメ。』とか、それほど融通のきかないものでもありませんので数学を嫌いにならないでください。

(2)
水族館でも見術館でも動物園でもどこでも良いです。

特別営業日の入館料は通常営業日の
　大人は\(\,2\,\)割引
　子どもは\(\,3\,\)割引
です。

通常営業日の
　大人の入館料を\(\,\color{red}{x}\,\)
　子どもの入館料を\(\,\color{red}{y}\,\)
とすると、
特別営業日の
　大人の入館料は\(\,\color{blue}{0.8x}\,\)
　子どもの入館料は\(\,\color{blue}{0.7y}\,\)
となります。

⇒　割合と歩合と百分率の使い方と定価(値段)の文字式

文字が2つなので、条件から2つ方程式を立てれば求まります。

　・通常営業日に大人\(\,1\,\)人と子ども\(\,1\,\)人で\(\,\color{red}{3600}\,\)円
　・特別襟業日に大人\(\,2\,\)人と子ども\(\,3\,\)人で\(\,\color{blue}{6510}\,\)円

これを方程式にすると、

　\( \begin{cases}
\hspace{7pt} x+y=\color{red}{3600}\\ \\
\hspace{7pt} 0.8x\times 2+0.7y\times 3=\color{blue}{6510}
\end{cases}\)

左辺を整理して

　　\( \begin{cases}
\hspace{7pt} x+y=3600\\ \\
\hspace{7pt} 1.6x+2.1y=6510
\end{cases}\)

①　\(\,\underline{　x+y　}\,\)
②　\(\,\underline{　1.6x+2.1y　}\,\)

特別営業日の割引後の入館料を分数で表すと、
　大人　\(\displaystyle \frac{8}{10}x\)
　子ども　\(\displaystyle \frac{7}{10}y\)
となり、この場合は

②　\(\displaystyle \underline{　\frac{16}{10}x+\frac{21}{10}y}　\)

となりますがどちらも適切な表現ですので問題ありません。

計算処理でもどちらも両辺\(\,10\,\)倍して、
結果同じ方程式になりますので時間的な差もありません。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

上の連立方程式を解くと、

　\(\hspace{15pt}16x+16y=57600\\
\underline{-\,)\,16x+21y=65100}\\
\hspace{36pt}-5y=-7500\\
\hspace{52pt}y=1500\)

このとき

　\(\begin{eqnarray}
x+1500&=&3600\\
x&=&2100
\end{eqnarray}\)

③　\(\,\underline{　2100　}\,\)　④　\(\,\underline{　1500　}\,\)

③④は通常営業日の入館料です。
特別入館日の料金は
　大人　\(2100\times 0.8=1680\)　円
　子ども　\(1500\times 0.7=1050\)　円

⑤　\(\,\underline{　1680　}\,\)　⑥　\(\,\underline{　1050　}\,\)

この問題はあれこれ考える前に、日本文を方程式にした方がはやいですね。

(3)
\(\,1\,\)から\(\,5\,\)までのカードが\(\,1\,\)枚ずつあり、続けて\(\,2\,\)枚引いて二桁の数字を作ります。

①
できる二桁の数字はいくつあるか。

樹形図ですぐに終わります。
同じ数字は並ばないのでできる二桁の数字は、
　\(\,12\,,\,13\,,\,14\,,\,15\,\)
　\(\,21\,,\,23\,,\,24\,,\,25\,\)
　\(\,31\,,\,32\,,\,34\,,\,35\,\)
　\(\,41\,,\,42\,,\,43\,,\,45\,\)
　\(\,51\,,\,52\,,\,53\,,\,54\,\)

答え　\(\,\underline{　20　通り　}\,\)

②
\(\,3\,\)の倍数になるのは各桁の数字の和が\(\,3\,\)の倍数になるときです。

⇒　覚えておいた方がいい倍数の見分け方

①の\(\,20\,\)通り中
　\(\,12\,,\,15\,,\,21\,,\,24\,,\,42\,,\,45\,,\,51\,,\,54\,\)
の\(\,8\,\)通り。

よって、求める確率は

　\(\displaystyle \frac{8}{20}=\underline{　\frac{2}{5}　}\)

\(\color{black}{\fbox{　2　}}\)はここまでですが、
\(\color{black}{\fbox{　1　}}\),\(\color{black}{\fbox{　2　}}\)の小問集合だけで全配点の\(\,42\,\)％あることは知っておきましょう。

長くなりますが、このまま続けます。

関数と面積と体積の融合問題

　\(\color{blue}{\fbox{　3　}}\)

関数問題です。
典型的な問題が並んでいるのでそれほど難しくは感じないでしょう。

(1)
\(\,\mathrm{A,B}\,\)の\(\,2\,\)点を通る直線があります。

①
　\(\,\mathrm{A\,(\,1\,,\,9\,)\,,\,B\,(\,-2\,,\,0\,)}\,\)
を通る直線
　\(y=ax+b　･･･ア\)
の傾き\(\,a\,\)と切片\(\,b\,\)を求める問題です。

傾きは変化の割合と同じで、
　\(\displaystyle (傾き)=\frac{　\color{red}{y\,の増加量}　}{　\color{blue}{x\,の増加量}　}\)
です。

　\(\,x\,の増加量=1-(-2)=\color{blue}{3}\,\)
　\(\,y\,の増加量=9-0=\color{red}{9}\,\)

なので傾き\(\,a\,\)は
　\(\displaystyle \,a=\frac{\color{red}{9}}{\color{blue}{3}}=\underline{　3　}\,\)

このとき関数は
　\(y=3x+b\)
となり、これは\(\,\mathrm{A,B}\,\)を通るのでどちらかを代入して、
（どっちでも良いです。ここでは\(\,\mathrm{A}\,\)を代入します。）

　\(\begin{eqnarray}
9&=&3\times (1)+b\\
&=&3+b\\
b&=&\underline{　6　}
\end{eqnarray}\)

\(\,x,y\,\)の増加量を出すときは\(\,x,y\,\)ともに同じ方向に引き算するように注意しておきましょう。

　\(\,(\hspace{6pt}\,1\,,\,9\,)\,\)
　\(\,(\,-2\,,\,0\,)\,\)

上から下を引いても良いし、下から上を引いても良いですが、
\(\,x\,\)成分と\(\,y\,\)成分で方向を変えると傾きの符号は逆になります。

(2)
\(\,\mathrm{△OAB}\,\)を\(\,x\,\)軸を軸として回転させたときの体積です。
円すいから円すいをくり抜いた形をしています。

座標上の点\(\,\mathrm{A}\,\)から\(\,x\,\)軸に下ろした垂線と\(\,x\,\)軸との交点を\(\,\mathrm{H}\,\)として、
底面の円を下に、頂点\(\,\mathrm{B}\,\)を上にして見ると
回転体は縦横の縮尺は違いますが図のようになります。

\(\,\mathrm{△ABH}\,\)を回転させた円すいは、
　底面の半径が\(\,\color{red}{9}\,\)で、高さが\(\,\color{magenta}{3}\,\)の円すい

\(\,\mathrm{△AOH}\,\)を回転させた円すいは、
　底面の半径が\(\,\color{red}{9}\,\)で、高さが\(\,\color{blue}{1}\,\)の円すい

なので、求める立体の体積は

　\(\hspace{10pt}\displaystyle \frac{1}{3}\times \pi (\color{red}{9})^2\times \color{magenta}{3}-\frac{1}{3}\times \pi (\color{red}{9})^2\times \color{blue}{1}\\
\displaystyle =81\,\pi-27\,\pi\\
\displaystyle =\underline{　54\,\pi　}　(\mathrm{cm^2})\)

底面積が同じなので高さの差だけかけても同じです。

　\(\hspace{10pt}\displaystyle \frac{1}{3}\times \pi\,(\color{red}{9})^2\times (\color{magenta}{3}-\color{blue}{1})\\
\displaystyle =\frac{1}{3}\times 81\,\pi \times 2\\
=\underline{　54\,\pi　}　(\mathrm{cm^2})\)

⇒　円錐(すい)の表面積や四角錐,五角錐の体積の求め方

錐体の表面積や体積の求め方は見直しておきましょう。

(2)
今度は放物線です。

①
関数は\(\,y=ax^2\,\)で比例定数が分かっていませんが、
　\(\,\mathrm{A\,(\,2\,,\,2\,)}\,\)
を通ることから、
　\(\begin{eqnarray}\displaystyle
2&=&a\times (2)^2\\
&=&4a\\
a&=&\underline{　\frac{1}{2}　}
\end{eqnarray}\)

比例定数が決まったので関数は
　\(\displaystyle \,y=\frac{1}{2}x^2\,\)

\(\,\mathrm{B}\,(\,-4\,,\,p\,)\,\)を通ることから関数に代入すると、
　\(\begin{eqnarray}
p&=&\frac{1}{2}\times (-4)^2\\
&=&\underline{　8　}
\end{eqnarray}\)

ここまではおまけ問題です。

②
定義域（\(\,x\,\)の変域）が\(\,-1\,≦\,x\,≦\,3\,\)のときの、
値域（\(\,y\,\)の変域）を求める問題です。

これもおまけ問題ですが、グラフを書いて確認しないと間違えますよ。

　\(\,x=-1\,\)　のとき　\(\displaystyle \,y=\frac{1}{2}\times (-1)^2=\color{magenta}{\frac{1}{2}}\,\)
　\(\,x=3\,\)　のとき　\(\displaystyle \,y=\frac{1}{2}\times (3)^2=\color{red}{\frac{9}{2}}\,\)
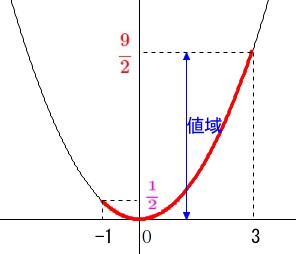ですが\(\,x=-1\,\)のときの値は値域（\(\,y\,\)の変域）には関係ありません。
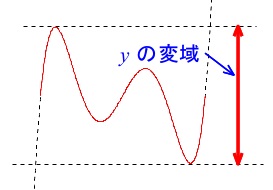値域は両端の値ではなく、定義域の範囲内での最小値と最大値の範囲です。

よって、グラフからも分かるとおり、求める\(\,y\,\)の変域は
　\(\displaystyle \underline{　0\,≦\,y\,≦\,\frac{9}{2}　}\)

\(\displaystyle \,1\,≦\,y\,≦\,\frac{9}{2}\,\)ではありません。

③
\(\,x\,\)軸上に点\(\,\mathrm{C}\,\)を\(\,\mathrm{A}\,\)の\(\,x\,\)座標より小さくとり、\(\,\mathrm{△ABC}\,\)をつくります。

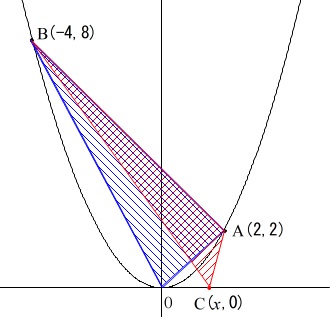
そのとき、
　\(\displaystyle \,\mathrm{△ABC=\frac{2}{3}△OAB}\,\)
となる点\(\,\mathrm{C}\,\)の座標を求めます。

点\(\,\mathrm{C}\,\)の\(\,x\,\)座標を\(\,x\,\)としておきます。

\(\,\mathrm{△OAB}\,\)の面積は具体的に求めると\(\,12\,\)なので、
\(\,\mathrm{△ABC}\,\)の面積が\(\,8\,\)となるように\(\,\mathrm{C}\,\)を決めることもできますが、
『覚え太郎』会員以外にはやりづらいだろうから面積比を利用して求めます。

直線\(\,\mathrm{AB}\,\)を表す\(\,1\,\)次関数は、
　\(y=-x+4\)
直線\(\,\mathrm{OA}\,\)を表す比例の関数は、
　\(y=x\)
なので、
直線\(\,\mathrm{AB}\,\)と直線\(\,\mathrm{OA}\,\)は垂直に交わっています。
垂直でなくても同じですが分かり易くするために書いておきます。

\(\,\mathrm{△OAB}\,\)と\(\,\mathrm{△ABC}\,\)が線分\(\,\mathrm{AB}\,\)を共通の底辺であるとすると、
\(\,\mathrm{△ABC}\,\)の高さが\(\,\mathrm{△OAB}\,\)の高さの\(\displaystyle \,\frac{2}{3}\,\)になれば良いわけです。
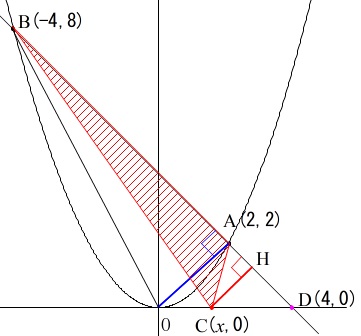直線\(\,\mathrm{AB}\,\)上に\(\,\mathrm{H}\,\)を\(\,\mathrm{CH}\,\)と\(\,\mathrm{BD}\,\)が垂直になるようにとります。

このとき、\(\displaystyle \,\mathrm{CH=\frac{2}{3}OA}\,\)となれば良いのです。

\(\,\mathrm{△DOA}\,\)　∽　\(\,\mathrm{△DCH}\,\)　なので、
　\(\,\mathrm{DO:DC=3:2}\,\)
となれば面積は\(\displaystyle \,\frac{2}{3}\,\)となるので、
点\(\,\mathrm{D}\,\)の座標が\(\,(\,4\,,\,0\,)\,\)であることから、

　\(\begin{eqnarray}\displaystyle
\mathrm{DO:DC}&=&3:2\\
4:(4-x)&=&3:2\\
3(4-x)&=&4\times 2\\
12-3x&=&8\\
-3x&=&-4\\
x&=&\frac{4}{3}　(\,x\,＜\,2\,)
\end{eqnarray}\)

よって求める点\(\,\mathrm{C}\,\)の座標は
　\(\,\mathrm{C}　\underline{　\displaystyle \left(\,\frac{4}{3}\,,\,0\,\right)　}\,\)

『覚え太郎』会員で公式（平面図形\(\,\mathrm{No.46}\,\)や座標と図形\(\,\mathrm{No.26}\,\)）を使って求めた人は答えが2つ同時に出てきたはずです。
この問題は\(\,\mathrm{C}\,\)が\(\,\mathrm{A}\,\)より小さい\(\,x\,\)座標と条件が付いているので答えは1つに絞られますが、
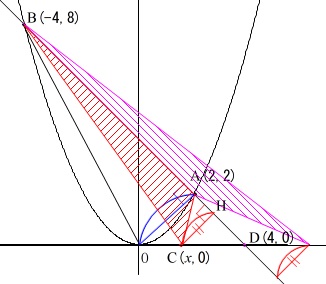\(\,\mathrm{A}\,\)の\(\,x\,\)座標より大きい三角形も考えると2つあるということです。