秋田県公立高校入試(2019年度)の数学第2問の問題と解説

秋田県で2019年（平成31年度)に行われた公立高校入試の数学第2問の問題と解説です。
第2問は放物線と双曲線の関数、1次方程式の立式と解、および規則性の基本問題の小問集合となっています。
基本問題が並んでいるだけで時間もかかりませんので確実に得点しておきましょう。

問題は秋田県で公開してくれています。

⇒　2019年(平成31年)度秋田県公立高校入試数学問題

関数と方程式と規則性

\(\,　\large{2}　\,\)は放物線と双曲線の交点と直線、1次方程式の立式と解、それと規則性の基本の小問集合です。

関数の基本問題

(1)
2つの関数で、放物線の比例定数は分かっていませんが、反比例の比例定数が与えられているので交点の座標が求まります。

①
問題の条件から
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-2\,\)
　\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,3\,\)

\(\,\mathrm{A,B}\,\)ともに双曲線\(\,\displaystyle y=-\frac{12}{x}\,\)上の点なので
　\(\mathrm{A}\,(\,-2\,,\,6\,)\)
　\(\mathrm{B}\,(\,3\,,\,-4\,)\)
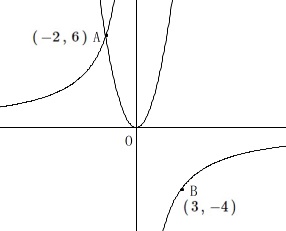放物線を表す\(\,y=ax^2\,\)は点\(\,\mathrm{A}\,\)を通るので、

　\(\begin{eqnarray}
6&=&a\times (-2)^2\\
6&=&4a\\
a&=&\underline{　\frac{3}{2}　}
\end{eqnarray}\)

②
\(\,2\,\)点
　\(\mathrm{A}\,(\,\color{red}{-2}\,,\,\color{blue}{6}\,)\)
　\(\mathrm{B}\,(\,\color{red}{3}\,,\,\color{blue}{-4}\,)\)
を通る直線を求めます。

傾きは変化の割合に等しいので
　\(\begin{eqnarray}\displaystyle
(傾き)&=&\frac{　y\,の増加量　}{　x\,の増加量　}\\
&=&\frac{\,(\color{blue}{-4})-(\color{blue}{6})\,}{\,\color{red}{3}-(\color{red}{-2})}\\
&=&\frac{-10}{5}\\
&=&\color{red}{-2}
\end{eqnarray}\)

傾きが分かれば求める直線は
　\(y=\color{red}{-2}x+b\)
とおけるので、この直線が通る点\(\,\mathrm{A}\,\)か点\(\,\mathrm{B}\,\)を代入します。
　\(\mathrm{B}\,(\,\color{red}{3}\,,\,\color{blue}{-4}\,)\)
を代入しましょう。

　\(\begin{eqnarray}
\color{blue}{-4}&=&-2\times (\color{red}{3})+b\\
-4&=&-6+b\\
b&=&2
\end{eqnarray}\)

よって、\(\,2\,\)点\(\,\mathrm{A,B}\,\)を通る直線は
　\(\underline{　y=-2x+2　}\)

1つ関数が決まっていれば\(\,x\,\)座標が与えられるなら\(\,y\,\)座標は求めておくことです。
\(\,y\,\)座標が与えられている場合も\(\,x\,\)座標は求めておくようにしましょう。

方程式の立式と解

(2)
料金について方程式を立てて解きます。

問題の指定通り\(\,x\,\)枚プリントするとします。

\(\,\mathrm{A}\,\)店では\(\,1\,\)枚につき\(\,24\,\)円なので\(\,x\,\)枚プリントすると
　\(\,24x　(円)　･･･①\,\)

\(\,\mathrm{B}\,\)店では\(\,30\,\)枚までは\(\,1\,\)枚につき\(\,30\,\)円、
\(\,31\,\)枚目からは\(\,15\,\)円なので、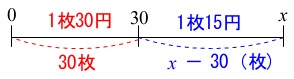\(\,x\,\)枚プリントするとすると
\(\,x\,≧\,31\,\)として、

　\(\hspace{10pt}30\times 30+15\times (x-30)\\
=900+15x-450\\
=15x+450　(円)　･･･②\)

\(\,\mathrm{A}\,\)店と\(\,\mathrm{B}\,\)店で同じ料金になるのは、
①と②が等しくなるときなので

　\(\begin{eqnarray}
24x&=&15x+450\\
9x&=&450\\
x&=&50
\end{eqnarray}\)

\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　50　}\,\)

(3)
長方形を重ねたときの枚数と面積の規則性です。

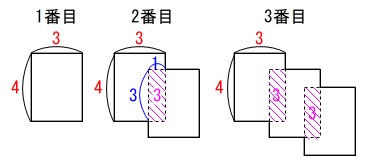
①
\(\,4\,\)番目の図形なので具体的に書いて計算すれば良いだけです。
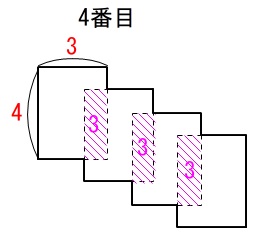求め方はいろいろありますが、
良くある問題なのでバラバラから重なりを引くという方法にしましょう。
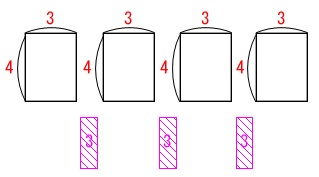長方形\(\,4\,\)枚から重なり3つを引いて、

　\(\hspace{10pt}\color{red}{4\times 3}\times 4-\color{magenta}{3}\times 3\\
=48-9\\
=\underline{　39　}　(\mathrm{cm^2})\)

重なっている部分の面積は1つの重なりについて\(\,1\,\)回引けば良いだけですよ。

②
具体的に規則性を見ていくと

　\(\,1\,\)枚のときは重なりが\(\,0\,\)
　\(\,2\,\)枚のときは重なりが\(\,1\,\)
　\(\,3\,\)枚のときは重なりが\(\,2\,\)
　\(\,4\,\)枚のときは重なりが\(\,3\,\)
　\(\hspace{10pt}\cdots\)
　\(\,\color{red}{n}\,\)枚のときは重なりが\(\,\color{red}{n-1}\,\)

この規則性が見えていれば一般的な文字を使って面積を表せます。

バラバラな\(\,n\,\)枚の長方形の面積から重なり部分\(\,\color{red}{(n-1)}\,\)個の面積を引くという考え方から、
　\(\,1\,\)枚の長方形の面積は\(\,\color{red}{12}\,\)
　重なり部分の面積は\(\,\color{magenta}{3}\,\)
なので、\(\,n\,\)番目の図形の面積は、

　\(\hspace{10pt}\color{red}{12}\times n-\color{magenta}{3}\times (n-1)\\
=12n-3n+3\\
=\color{red}{9n+3}\)

答え
　\(\color{black}{\fbox{　ア　}}\)　\(\,\underline{　12　}\,\)
　\(\color{black}{\fbox{　イ　}}\)　\(\,\underline{　n-1　}\,\)
　\(\color{black}{\fbox{　ウ　}}\)　\(\,\underline{　9n+3　}\,\)

規則性問題では規則性が見えてくるまで具体的に書く、ということが大きな差がつくポイントです。

\(\,　\large{2}　\,\)はこれだけです。
短いですがここで区切ります。笑

⇒　秋田県公立高校入試(2019年度)の数学問題第3問と第4問の解説

\(\,　\large{3}　\,\)は作図と平面図形の基本性質
\(\,　\large{4}　\,\)はデータの活用と確率です。

⇒　2019年(平成31年)度秋田県公立高校入試の数学の第1問の解説

問題\(\,　\large{1}　\,\)は計算中心の小問集合です。

\(\,　\large{1}　,　\large{2}　\,\)だけで\(\,100\,\)点満点中の\(\,57\,\)点分の配点がされています。
ここまでで落とす問題がないように、基本はしっかり抑えておきましょう。

⇒　秋田県公立高校入試(2019年度)の数学第5問(選択問題)の解説

\(\,　\large{5}　\,\)は受験する高校が指定する選択問題です。
本試験では間違えないようにしましょう。