秋田県公立高校入試(2019年度)の数学問題第3問と第4問の解説

秋田県で2019年（平成31年度)に行われた公立高校入試の数学第3問と第4問の問題と解説です。
第3問は接線の作図の方法と内接する円と外接する三角形の性質問題です。
第4問は簡単なデータの活用と確率です。
文字数は多いですが図がたくさん書いてあるので利用すればそれほど時間はかかりません。

問題は秋田県で公開してくれています。

⇒　2019年(平成31年)度秋田県公立高校入試数学問題

接線の作図と内接する円および外接する円の性質

円の外部の点から円に接する接線の作図方法と、
円に外接する三角形の性質および円に内接する四角形の見分け方の問題です。

(2)で長さを求める問題がありますが、相似に気がつけば簡単に求まります。
ただし、相似を見つけるまでに図形問題解決の基本的な作業がありますので確認しておくと良いでしょう。

接線の作図方法

円の外部の点から円に接する接線を作図するには「接点」を決めなくてはなりません。
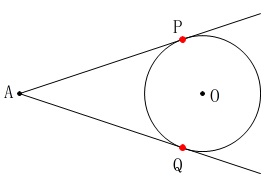適当に接するように引いた線は接しているようには見えますが、
正確に接点を通っているとは言えません。図のように接線を引いたつもりでも拡大してみるとずれているかもしれないからです。

そこで、作図では理由を付けて（論理的に）接線であることを示します。

できあがった図が実際にむちゃくちゃ正確である必要はありませんよ。
手書きで書くことになるので完全な図は書けません。
鉛筆の線には太さがあるので実際には多少のズレはあるかもしれませんが、理由を付けていればずれていないように見えれば良いです。

(1)
①
結果から考えれば見えてきます。
円\(\,\mathrm{O}\,\)の周上の点\(\,\mathrm{P,Q}\,\)が、
\(\,\mathrm{A}\,\)から引いた接線の接点になるためには、
　\(\,\mathrm{∠APO=∠AQO=90^{\circ}}\,\)
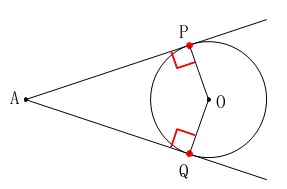となれば良いのです。

\(\,90°\,\)の作図は\(\,180°\,\)の二等分線という考えもできますが、直線（接線）が定まっていないのでできません。
そこで、
　直径に対する円周角が\(\,90°\,\)になる
という性質を利用して作図します。

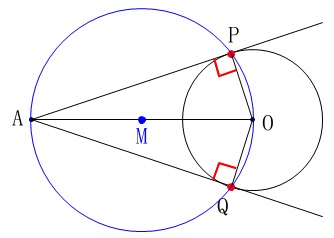
つまり、
　線分\(\,\mathrm{AO}\,\)を直径とする円を書いて、
　その円周上に\(\,\mathrm{P,Q}\,\)をとる、
ということです。

線分\(\,\mathrm{AO}\,\)を直径とする円を描くには、
線分\(\,\mathrm{AO}\,\)の中点である中心\(\,\mathrm{M}\,\)が必要です。

前置きが長くなりましたが、作図に必要なことは簡単です。

中心\(\,\mathrm{M}\,\)が決まれば点\(\,\mathrm{M}\,\)から\(\,\mathrm{AM}\,\)または\(\,\mathrm{OM}\,\)を半径とする円を書けば良いので、
　線分\(\,\mathrm{AO}\,\)を引いて、

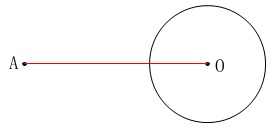
　線分\(\,\mathrm{AO}\,\)の垂直二等分線と\(\,\mathrm{AO}\,\)との交点を中心\(\,\mathrm{M}\,\)として

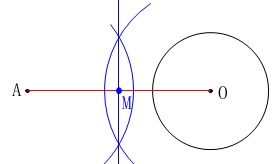
　点\(\,\mathrm{M}\,\)を中心として半径\(\,\mathrm{AM}\,\)の円を書いて、交点を\(\,\mathrm{P,Q}\,\)とする。

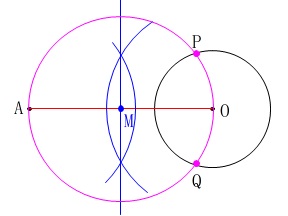
　答え　\(\,\underline{　ウ　}\,\)　→　\(\,\underline{　ア　}\,\)　→　\(\,\underline{　イ　}\,\)

三角形の合同の証明と合同な三角形の性質

②
点Aから接点までの距離が等しいこと、
　\(\,\mathrm{AP=AQ}\,\)
を証明します。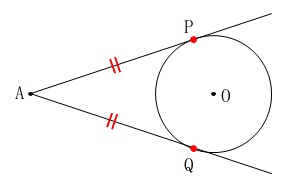
　\(\,\mathrm{△APO　≡　△AQO}\,\)
を言えば良いだけです。

合同でも相似でも「証明は図の中で終わらせておく！」ですよね。
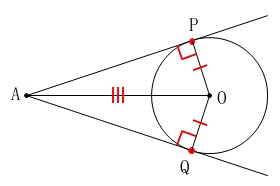　半径は常に等しく、
　接点と中心を結ぶ半径は接線と\(\,90°\,\)、
　線分\(\,\mathrm{AO}\,\)は共通の線分、
なので直角三角形の合同条件がそろいます。

（証明）
　\(\,\mathrm{△APO}\,\)と\(\,\mathrm{△AQO}\,\)において
半径は等しいので
　\(\,\mathrm{OP=OQ　･･･(ア)}\,\)
線分\(\,\mathrm{AO}\,\)は共通の辺なので
　\(\,\mathrm{AO=AO　･･･(イ)}\,\)
また\(\,\mathrm{AP}\,\)および\(\,\mathrm{AQ}\,\)は接線なので
　\(\,\mathrm{∠APO=∠AQO=90°　･･･(ウ)}\,\)
(ア)(イ)(ウ)より
　直角三角形の斜辺と他の\(\,1\,\)辺が等しい
から
　\(\,\mathrm{△APO　≡　△AQO}\,\)
合同な図形の対応する辺は等しいので、
　\(\,\mathrm{AP=AQ}\,\)
（証明終わり）

直角三角形の合同条件を使うときは、
(ウ)の角度が等しいところで\(\,90°\,\)であることを抜かさないようにしましょう。

円に外接する三角形の性質と四角形が円に内接する条件

③
円\(\,\mathrm{O}\,\)が三角形の内接円になる場合です。
（内接円とは円が三角形の\(\,3\,\)辺と接している円のことです。）
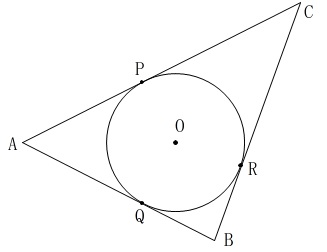反対に見れば、三角形が円\(\,\mathrm{O}\,\)に外接していることと同じです。

②で三角形の合同を示したことを利用します。
辺\(\,\mathrm{AB,BC,CA}\,\)は円\(\,\mathrm{O}\,\)に接しているので、

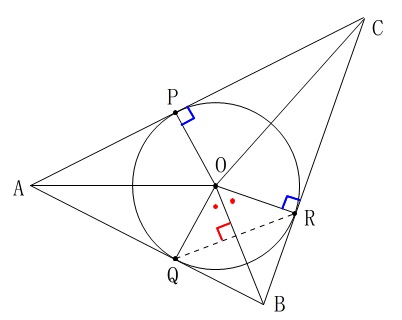
　\(\,\mathrm{△BQO　≡　△BRO}\,\)
なので、
　\(\,\mathrm{∠BOQ=∠BOR}\,\)
\(\,\mathrm{△OQR}\,\)は二等辺三角形で頂角の二等分線は底辺を垂直に\(\,2\,\)等分するので、
　\(\,\mathrm{　\color{red}{BO　⊥　QR}　}\,\)

また、
　\(\,\mathrm{∠OPC=∠ORC=90°}\,\)
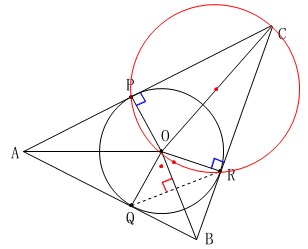だから
　\(\,\mathrm{△OPC}\,\)と\(\,\mathrm{△ORC}\,\)はどちらも\(\,\mathrm{OC}\,\)を直径とする円に内接している
ので、
　\(\,4\,\)点\(\,\mathrm{C,P,O,R}\,\)は1つの円周上にある
ことが言えます。

※
対角の和が\(\,180°\,\)である時点で四角形\(\,\mathrm{CPOR}\,\)は円に内接していることは分かります。

答え　\(\,\underline{　イ　,　エ　}\,\)

辺の長さも角度も固定されていないので、
極端な例を考えて見たらすぐに分かります。

　\(\,\mathrm{AB=BC\,,\,AC \,/\!/\, QR}\,\)
は必ず成り立つとは言えません。

四角形の4辺が円に接するときの性質と線分の長さ

(2)
線分\(\,\mathrm{AO}\,\)の長さを求めます。

条件は
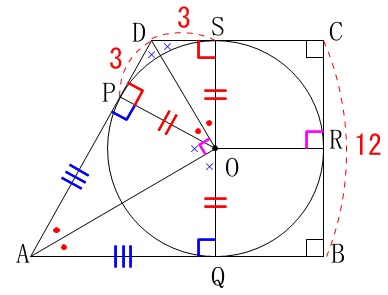
　点\(\,\mathrm{P,Q,R,S}\,\)は接点
　\(\,\mathrm{∠ABC=∠BCD=90°}\,\)
　\(\,\mathrm{BC=12}\,\)
　\(\,\mathrm{DS=3}\,\)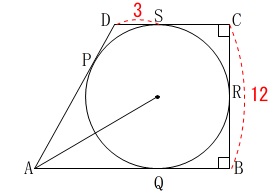接線が\(\,4\,\)本に増えますが(1)の②で証明したことから分かるように合同な三角形が増えるだけです。

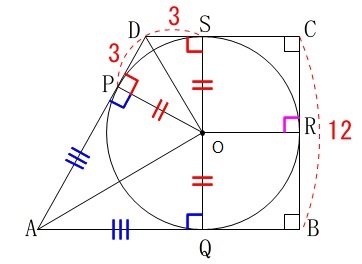証明で利用したように等しい辺は分かります。
また、合同なので対応する角も等しいので、
　\(\,\mathrm{∠SOD=∠POD}\,\)
　\(\,\mathrm{∠POA=∠QOA}\,\)．

さらに四角形\(\,\mathrm{CBQS}\,\)は長方形なので、
（四角形\(\,\mathrm{ORCS}\,\)と\(\,\mathrm{OQBR}\,\)は\(\,1\,\)辺\(\,6\,\)の正方形です。）
　\(\,\mathrm{∠SOQ=180°}\,\)
このことから相似な三角形が見つかります。

合同な三角形が2つ並んでいるので、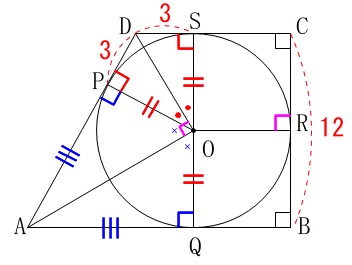　\(2(\color{red}{●}＋\color{blue}{×})=180^{\circ}\)
このことから
　\(\begin{eqnarray}
\mathrm{∠AOD}&=&\color{red}{●}+\color{blue}{×}\\
&=&90°
\end{eqnarray}\)

また、直角三角形では1つの角が\(\,90°\,\)なので、
残りの2つ角の和は\(\,90°\,\)になります。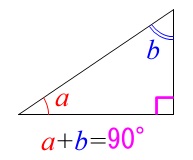相似な三角形が見えてきました。
　\(\,\mathrm{△OSD}\)　∽　\(\mathrm{△AQO}\,\)
です。

半径\(\,\mathrm{OS=OQ=\color{red}{6}}\,\)なので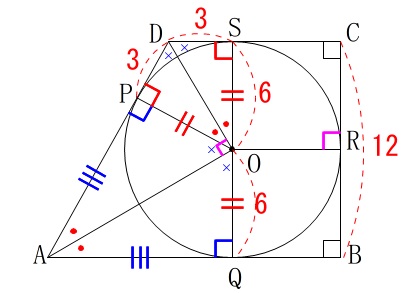
　\(\begin{eqnarray}\displaystyle
\mathrm{OS:AQ}&=&\mathrm{SD:QO}\\
6:\mathrm{AQ}&=&3:6\\
3\times \mathrm{AQ}&=&6\times 6\\
\mathrm{AQ}&=&\frac{6\times 6}{3}\\
&=&\color{blue}{12}
\end{eqnarray}\)
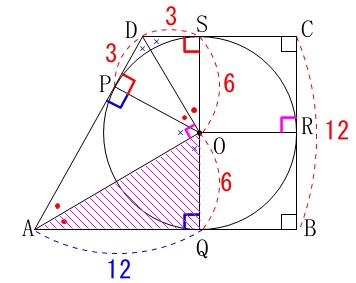直角三角形\(\,\mathrm{AQO}\,\)に三平方の定理を利用して、

　\(\begin{eqnarray}\displaystyle
\mathrm{AO^2}&=&\mathrm{AQ^2+OQ^2}\\
&=&\color{blue}{12}^2+\color{red}{6}^2\\
&=&144+36\\
&=&180\\
\mathrm{AO}&=&\pm 6\sqrt{5}
\end{eqnarray}\)

よって線分\(\,\mathrm{AO}\,\)は、\(\,\mathrm{AO\,＞\,0}\,\)なので、

　\(\mathrm{AO}=\underline{　6\sqrt{5}　}\)

ちょっと説明がくどいですね。
見慣れた三角形の相似なのですぐに見つかるでしょう。

\(\,\mathrm{BC}=12\,\)だから\(\,\mathrm{AQ＝12}\,\)になるとは限りませんよ。
\(\,\mathrm{DS＝6}\,\)のときには\(\,\mathrm{ABCD}\,\)は正方形で\(\,\mathrm{AQ=6}\,\)です。

\(\,　\large{4}　\,\)もあるので\(\,　\large{3}　\,\)はサクッと終わらせたかったのですが長くなりました。
\(\,　\large{4}　\,\)はサクッと終わらせます。笑

データの活用と確率

\(\,　\large{4}　\,\)は度数分布表の読み取りと簡単な確率問題です。

相対度数分布表とヒストグラム

(1)
\(\,30\,\)人のデータが2つ（\(\,2\,\)組分）あります。

①
相対度数分布表の中の数値を求めます。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

度数分布表と同じようなものですが、見て感覚で分かるヒストグラムも復習しておくと良いです。

\(\,3\,\)年生\(\,60\,\)人の通学時間の度数分布表です。
　\(\begin{array}{|c|c|c|} \hline
　階級　&　度数　&　相対度数　\\ \hline
0～10 & 6 & 0.10 \\ \hline
10～20 & x & 0.30 \\ \hline
20～30& 21 & y \\ \hline
30～40 & 12 & 0.20 \\ \hline
40～50 & 3 & 0.05 \\ \hline
　計　& 60 & 1.00 \\ \hline
\end{array}\)

相対度数はその階級の度数を度数合計でわった数なので、

　\(\displaystyle (\color{red}{相対度数})=\frac{　(\color{blue}{度数})　}{　(度数合計)　}\)
または、
　\((\color{blue}{度数})=(度数合計)\times (\color{red}{相対度数})\)
となるので、
　\(\begin{eqnarray}\displaystyle
x&=&60\times 0.30\\
&=&\underline{　18　}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
y&=&\frac{21}{60}\\
&=&\underline{　0.35　}
\end{eqnarray}\)

②
階級と中央値についてです。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

入試までに忘れがちになる代表値は復習から外すことはできませんよ。

\(\,30\,\)人のデータの中央値は小さい順、大きい順に並べたときの
　\(\,15\,\)人目と\(\,16\,\)人目の平均値
になります。

①で具体的な数値が入りましたが、度数分布表は全体のデータなので組ごとのデータではありません。

組ごとのデータはヒストグラムを見ます。

\(\,3\,\)年\(\,1\,\)組は小さい方から見ると、
　\(\,20\,\)分未満の人が\(\,1+6=\color{red}{7}\,\)人
　\(\,20\,\)分以上\(\,30\,\)分未満の階級に\(\,\color{red}{11}\,\)人
となっているので、小さい方から\(\,15\,\)番目と\(\,16\,\)番目の人はどちらも

　\(\,20\,\)分以上\(\,30\,\)分未満の階級

にいます。

\(\,3\,\)年\(\,2\,\)組は小さい方から見ると、
　\(\,0\,\)分以上\(\,10\,\)分未満の階級に\(\,\color{blue}{5}\,\)人
　\(\,10\,\)分以上\(\,20\,\)分未満の階級に\(\,\color{blue}{12}\,\)人
となっているので、小さい方から\(\,15\,\)番目と\(\,16\,\)番目の人はどちらも

　\(\,10\,\)分以上\(\,20\,\)分未満の階級

にいます。

よって、\(\,3\,\)年\(\,1\,\)組の方が中央値は大きい、です。

答え　\(\,\underline{　ア　}\,\)

中央値を求める必要はありませんが、
　\(\,3\,\)年\(\,1\,\)組の中央値は\(\,25\,\)分
　\(\,3\,\)年\(\,2\,\)組の中央値は\(\,15\,\)分
と階級の真ん中の値になります。　

樹形図を書き出して確率を求めるシンプルな問題

樹形図でも良いので書いてみて下さい。
説明は必要無いほど簡単な問題です。笑

ここでは表にします。

　\(\begin{array}{|c|c|c|c|} \hline
　\mathrm{A}　&　\mathrm{B}　&　\mathrm{C}　&　結果　\\ \hline
-1 & -& +1 & \color{red}{-2} \\ \hline
-1 & – & -3 & +2 \\ \hline
-1 & × & +1 & \color{red}{-1} \\ \hline
-1 & × & -3 & +3 \\ \hline
+2 & – & +1 & +1 \\ \hline
+2 & – & -3 & +5 \\ \hline
+2 & × & +1 & +2 \\ \hline
+2 & × & -3 & \color{red}{-6} \\ \hline
\end{array}\)

\(\,8\,\)通りの計算があって、そのうち3通りが負の数になるので

答え　\(\displaystyle \underline{　\frac{3}{8}　}\)

\(\,　\large{3}\,,\,\large{4}　\,\)はここまでです。
説明は長いけど、自分で解くとすぐ終わりますよ。

⇒　秋田県公立高校入試(2019年度)の数学第5問(選択問題)の解説

\(\,　\large{5}　\,\)は高校別の選択問題です。

⇒　2019年(平成31年)度秋田県公立高校入試の数学の問題と解説

\(\,\large{1}\,\)の解説になります。

\(\,　\large{1}\,,\,\large{2}\,　\)は\(\,6\,\)割近い配点がある小問集合です。
\(\,　\large{3}\,,\,\large{4}\,\)もとりやすい問題なので高得点は十分狙えます。