2019年(平成31年)度秋田県公立高校入試の数学の問題と解説

2019年(平成31年)度に秋田県で行われた公立高校入試の数学の問題と解説です。
2018年度と同じように学校により選択問題があります。
選択する問題は受験する高校の指定した問題を解くことを忘れないようにしましょう。

問題は秋田県で公開していくれています。

⇒　2019年(平成31年)度の秋田県公立高校入試の数学問題

選択小問集合

　\(\,\large{1}\,\)

\(\,15\,\)問の中から学校によって指定された問題を\(\,8\,\)問答えます。
秋田県の受験生は十分ご存じだとは思いますが間違えないように念のためお伝えしておきます。

式の計算と比例式

(1)
分数と小数のかけ算です。
小数で計算しても大した計算ではありませんが、分数に統一した方が早くてミスは減ります。

　\(\hspace{10pt}\displaystyle \frac{5}{6}\times (-0.4)\\
\displaystyle =\frac{5}{6}\times \left(-\frac{4}{10}\right)\\
\displaystyle =\underline{　-\frac{1}{3}　}\)

(2)
展開して同類項をまとめるだけです。

　\(\hspace{10pt}2(3a-2b)-3(2a-b)\\
=6a-4b\color{red}{-6a+3b}\\
=\underline{　-b　}\)

暗算できる計算ではありますが\(\,2\,\)行目は符号ミスを減らすために書いた方が良いです。
暗算した方がはやいと勘違いしている人がいますが、書いた方がミスは減るし早いです。笑

(3)
単なる比例式です。
　\(\,(内項の積)=(外項の積)\,\)
を利用しましょう。

　\(\begin{eqnarray}\displaystyle
6:8&=&x:20\\
8x&=&6\times 20\\
x&=&\frac{6\times 20}{8}\\
&=&\underline{　15　}
\end{eqnarray}\)

かけ算部分は先に計算しても良いですが、どっちみち割り算しますので約分した方が楽です。

１次方程式と連立方程式と２次方程式

(4)
分数の方程式では最初に分母を無くすと早いです。

　\(\begin{eqnarray}\displaystyle
\frac{3x+4}{\color{red}{2}}&=&4x\\
3x+4&=&4x\times \color{red}{2}\\
3x+4&=&8x\\
3x-8x&=&-4\\
-5x&=&-4\\
x&=&\underline{　\frac{4}{5}　}
\end{eqnarray}\)

これを分数の計算で進める人はいないでしょうが、どんな方程式でも同じようにすれば良いです。

(5)
連立方程式を解くときの基本は一文字消去です。

　\( \begin{cases}
\hspace{7pt} 2x+3y=-1　･･･①\\
\hspace{7pt} -4x-5y=-1　･･･②
\end{cases}\)

この問題は加減法ですね。

\(\,y\,\)を消去しようとすると両方を何倍かしなければ係数がそろわないので\(\,x\,\)を消去します。
　\(2x+3y=-1　･･･①\)
両辺を\(\,2\,\)倍して、
　\(4x+6y=-2　･･･①’\)
これと連立された下の方程式②を両辺足します。
\(\,①’+②\,\)です。

　\(\hspace{26pt}4x+6y=-2\\
\underline{+\,)\,-4x-5y=-1}\\
\hspace{55pt}y=-3\)

これを①①’②のどれかに代入すれば\(\,x\,\)が求まります。
①に代入します。

　\(\begin{eqnarray}
2x+3\times (-3)&=&-1\\
2x-9&=&-1\\
2x&=&8\\
x&=&4
\end{eqnarray}\)

答え　\(\,\underline{　x=4\,,\,y=-3　}\,\)

(6)
「\(\,2\,\)次方程式の解を求める」ことと「\(\,2\,\)次方程式を解く」ことは同じことです。

⇒　方程式の解とは？2次方程式の係数と他の解を求める代入問題の解き方

左辺が因数分解できるか先に試しますが、
中学生にはきびしい「タスキガケ」になりますので解の公式で求めます。

　\(\color{red}{a}x^2+\color{blue}{b}x+\color{magenta}{c}=0\)
の解は（解の公式）
　\(\hspace{10pt}\displaystyle \frac{-\color{blue}{b}\pm \sqrt{\,\color{blue}{b}^2-4\color{red}{a}\color{magenta}{c}\,}}{2\color{red}{a}}\)
です。

　\(3x^2-5x+2=0\)
の解は
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-5)\pm \sqrt{(5)^2-4\times 3\times 2}}{2\times 3}\\
&=&\frac{5\pm \sqrt{25-24}}{6}\\
&=&\frac{5\pm 1}{6}\\
&=&\frac{5+1}{6}\,,\,\frac{5-1}{6}\\
&=&\underline{　1\,,\,\frac{2}{3}　}
\end{eqnarray}\)

\(\,2\,\)次方程式の左辺は
　\(\begin{eqnarray}
3x^2-5x+2&=&0\\
(x-1)(3x-2)&=&0
\end{eqnarray}\)
と因数分解できるので解は公式を使わなくても求まりますが、
タスキガケ因数分解を習うのは高校数学ということになっています。

⇒　高校の因数分解公式一覧　たすき掛けや手順（やり方）

※当会の高校数学サイトに移動します。

無理数の計算と比例関数の性質

(7)
素因数分解と分母の有理化です。

　\(\hspace{10pt}\displaystyle \sqrt{24}-\frac{18}{\sqrt{6}}\\
\displaystyle =\sqrt{\color{red}{2^2}\times 6}-\frac{18\times \color{blue}{\sqrt{6}}}{\sqrt{6}\times \color{blue}{\sqrt{6}}}\\
\displaystyle =\color{red}{2}\sqrt{6}-\frac{18\sqrt{6}}{6}\\
=2\sqrt{6}-3\sqrt{6}\\
=\underline{　-\sqrt{6}　}\)

説明しなくても良いでしょう。
無理数の計算を苦手にしている人は徹底的に練習しておいた方が良いです。
数字の世界が広がっているのですべての分野で答えまで届きにくくなります。

(8)
比例の関数で比例定数が負の場合の性質です。
比例は原点を通る\(\,1\,\)次関数です。
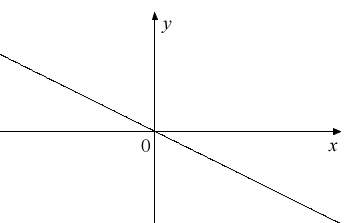グラフを書いてみれば必ず（一般的に）言えることはすぐに分かるでしょう。

比例定数が\(\,a\,＜\,0\,\)なのでグラフの傾きが右下がりになります。
\(\,x\,\)が増加する（右に移動する）と\(\,y\,\)は減少（下に下がる）します。

答え　\(\,\underline{　イ\,,\,ウ　}\,\)

有効数字と自然数の個数の求め方

(9)
有効数字\(\,3\,\)桁で表すだけです。

⇒　有効数字とは？桁(けた)数と四捨五入の方法と表し方(中1資料)

整数部分を一桁にして、小数点が元の位置からいくつ移動したかだけ見れば良いですよ。

　\(\hspace{10pt}6150=\underline{　6.15\times 10^3　}\)

(10)
ルートが付いていると考えにくいだろうからルートを外しましょう。

\(\,n\,,\,\mathrm{N}\,\)ともに自然数なので、
　\(\mathrm{N}\,≦\,\sqrt{n}\,＜\,\mathrm{N}+1\)
は全辺を\(\,2\,\)乗して
　\(\mathrm{N^2}\,≦\,n\,＜\,(\mathrm{N}+1)^2\)
としても成り立ちます。

この不等式を満たす\(\,n\,\)の個数は、
　\(\hspace{10pt}(\mathrm{N}+1)^2-\mathrm{N}^2\)
です。

これはすぐには分からないかもしれませんが、いくつか試して見れば良いのです。
例えば、\(\,\mathrm{N＝1}\,\)のとき、
　\(\hspace{10pt}1^2\,≦\,n\,＜\,(1+1)^2\)
で
　\(\hspace{10pt}1\,≦\,n\,＜\,4\)
を満たす自然数\(\,n\,\)は\(\,1,2,3\,\)の3個です。
これは
　\(\hspace{10pt}(1+1)^2-(1)^2\\
=2^2-1\\
=3\)
と同じです。

\(\,a\,\)から\(\,b\,\)までの整数の数は
　\(\hspace{10pt}b-a\color{red}{+1}\)
と\(\,\color{red}{1}\,\)を足す必要がありますが、
これは\(\,a\,≦\,n\,≦\,b\,\)を満たす整数の個数です。

ここでは
　\(\mathrm{N^2}\,≦\,n\,＜\,(\mathrm{N}+1)^2\)
と右側の不等式には等号がないので引き算すれば良いだけなのです。

ということで\(\,n\,\)の個数が\(\,31\,\)個のとき、
　\(\begin{eqnarray}
(\mathrm{N}+1)^2-\mathrm{N}^2&=&31\\
\mathrm{N}^2+2\mathrm{N}+1-\mathrm{N}^2&=&31\\
2\mathrm{N}&=&30\\
\mathrm{N}&=&\underline{　15　}
\end{eqnarray}\)

答えだけ出すなら、調べ尽くして悪あがきするという手もあります。笑
　\(\begin{array}{|c|c|c|c|} \hline
\,\mathrm{N}\, & \,\mathrm{N}^2\, & \,(\mathrm{N}+1)^2\, &　nの個数　\\ \hline
10 & 100 & 121 & 21 \\ \hline
11 & 121 & 144 & 23 \\ \hline
12 & 144 & 169 & 25 \\ \hline
13 & 169 & 196 & 27 \\ \hline
14 & 196 & 225 & 29 \\ \hline
15 & 225 & 256 & \color{red}{31} \\ \hline
\end{array}\)

よって、\(\,\mathrm{N}=\underline{　15　}\,\)

作図と円周角の定理と平行線のなす角

(11)
\(\,30°\,\)の作図です。
角の二等分線で作れる角は\(\,180°\,,\,90°\,,\,45°\,\)などです。

\(\,30°\,\)は正三角形の1つの角の半分なので正三角形を\(\,2\,\)等分しても良いのですが、
\(\,90°\,\)があるので\(\,60°\,\)を引くと\(\,30°\,\)となることで作図しましょう。
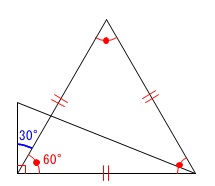つまり、\(\,\mathrm{BC}\,\)を\(\,1\,\)辺とする正三角形を作りながら直線\(\,\mathrm{BP}\,\)を作図すれば良いだけです。

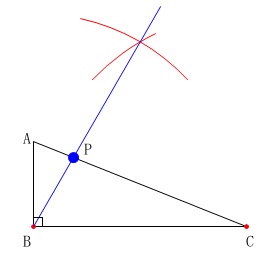
遠回りになりますが\(\,\mathrm{AB}\,\)を\(\,1\,\)辺とする正三角形を書いて、二等分線を利用しても作図できます。

(12)
中心角は円周角の\(\,2\,\)倍で、
半径は等しいので\(\,\mathrm{△OBC}\,\)は二等辺三角形になる、
それだけです。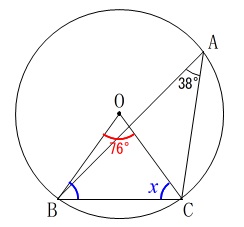中心角は円周角の\(\,2\,\)倍なので

　\(\begin{eqnarray}
\mathrm{∠BOC}&=&2\times \mathrm{∠BAC}\\
&=&2\times 38^{\circ}\\
&=&76^{\circ}
\end{eqnarray}\)

二等辺三角形の底角は等しいので、
頂角\(\,76^{\circ}\,\)の二等辺三角形の底角\(\,x\,\)は

　\(\begin{eqnarray}\displaystyle
x&=&\frac{180^{\circ}-76^{\circ}}{2}\\
&=&\frac{104^{\circ}}{2}\\
&=&\underline{　52^{\circ}　}
\end{eqnarray}\)

(13)
角度を求める問題は分かる角度をすべて書き出せば出てきます。
平行線では同位角と錯角が等しいので、

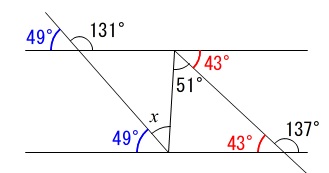
　\(\begin{eqnarray}
\color{blue}{49^{\circ}}+x&=&51^{\circ}+\color{red}{43^{\circ}}\\
49^{\circ}+x&=&94^{\circ}\\
x&=&94^{\circ}-49^{\circ}\\
&=&\underline{　45^{\circ}　}
\end{eqnarray}\)

念のために言っておくと、同位角と錯角はいつも等しいわけではありません。
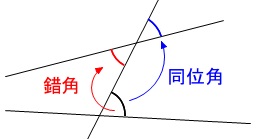\(\,2\,\)本の直線が平行線の場合だけ等しくなります。

正四角すいの体積と三角すいと四角すいの体積比

(14)
正四角錐の頂点から垂線を下ろすと、
底面の正方形の対角線の交点におります。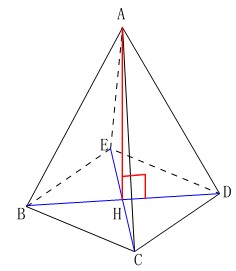底面の正方形\(\,\mathrm{BCDE}\,\)の対角線\(\,\mathrm{BD}\,\)の長さは

　\(\begin{eqnarray}
\mathrm{BD^2}&=&\mathrm{BC^2+DC^2}\\
&=&6^2+6^2\\
&=&72\\
\mathrm{BD}&=&\color{magenta}{6\sqrt{2}}　(\,\mathrm{BD}\,＞\,0\,)
\end{eqnarray}\)
\(\,\mathrm{H}\,\)は\(\,\mathrm{BD}\,\)の中点なので\(\,\mathrm{BH=\color{blue}{3\sqrt{2}}}\,\)だから、

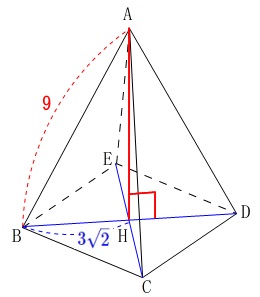
正四角錐\(\,\mathrm{A-BCDE}\,\)の高さ\(\,\mathrm{BH}\,\)は、
\(\,\mathrm{△ABH}\,\)に三平方の定理を利用して、

　\(\begin{eqnarray}
\mathrm{AB^2}&=&\mathrm{BH^2+AH^2}\\
9^2&=&(3\sqrt{2})^2+\mathrm{AH}^2\\
81&=&18+\mathrm{AH}^2\\
\mathrm{AH}^2&=&81-18\\
&=&63\\
\mathrm{AH}&=&3\sqrt{7}　(\,\mathrm{AH}\,＞\,0\,)
\end{eqnarray}\)

底面\(\,\mathrm{BCDE}\,\)は\(\,1\,\)辺\(\,6\,\)の正方形なので、
求める体積を\(\,\mathrm{V}\,\)とすると

　\(\begin{eqnarray}\displaystyle
\mathrm{V}&=&\frac{1}{3}\times 6^2\times 3\sqrt{7}\\
&=&\underline{　36\sqrt{7}　}　(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

(15)
三角錐（すい）と四角錐の体積比を求めますが、
\(\,\mathrm{B}\,\)から\(\,\mathrm{△ACD}\,\)に垂線を下ろすとその線分が両方の錐体の高さになります。
高さが同じなので底面積を比べるだけです。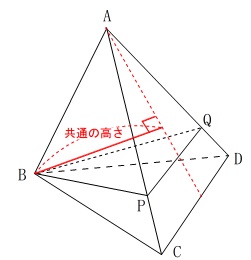底面になるのは\(\,\mathrm{△ACD}\,\)の中です。

問題に条件があります。

　\(\begin{eqnarray}
\mathrm{AP:PC}&=&\mathrm{AQ:QD}\\
&=&3:1
\end{eqnarray}\)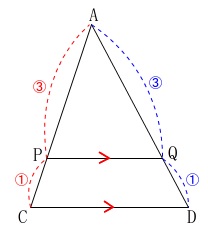
　\(\,\mathrm{△APQ}\,\)　∽　\(\,\mathrm{△ACD}\,\)
で、
　相似比が\(\,3:4\,\)
なので面積比は
　\(\hspace{10pt}3^2:4^2=\color{red}{9}:\color{magenta}{16}\)
となるので、
　\(\,\mathrm{△APQ:△ACD=\color{red}{9}:\color{blue}{7}}\,\)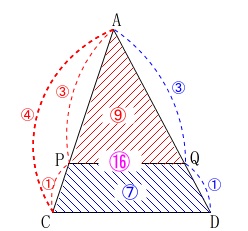
高さは同じなのでこの面積比が体積比となるので、
三角錐\(\,\mathrm{A-BPQ}\,\)の体積は、四角錐\(\,\mathrm{B-PCDQ}\,\)の体積の
　\(\hspace{10pt}\displaystyle \color{red}{9}\div \color{blue}{7}=\underline{　\frac{9}{7}　}　(倍)\)

\(\,　\large{1}　\,\)は以上ですが、\(\,15\,\)問中受験する高校が指定する\(\,8\,\)問を解くことは忘れないでください。
解き始める前に解く問題番号に大きく\(\,\color{red}{○}\,\)を付けるか、解かない問題に大きく\(\,\color{red}{×}\,\)を付けるかしておく方が良いですね。

一気に進めても良いのですが、一度にまとめると「長い」と言われるのでここでいったん区切ります。

⇒　秋田県公立高校入試(2019年度)の数学第2問の問題と解説

\(\,　\large{2}　\,\)は関数、方程式、規則性の基本問題の小問集合です。

⇒　秋田県公立高校入試(2019年度)の数学問題第3問と第4問の解説

\(\,　\large{3}　\,\)は作図と平面図形の性質です。
\(\,　\large{4}　\,\)はデータの活用と確率です。
選択ではなく問題もそれほど考えることがないのでまとめて良いでしょう。

⇒　秋田県公立高校入試(2019年度)の数学第5問(選択問題)の解説

\(\,　\large{5}　\,\)は選択問題で\(\,2\,\)問あるので選択を間違えないようにしましょう。

⇒　秋田県公立高校入試2018数学の過去問と解説

\(\,2018\,\)年度の問題も同じような構成ですが、秋田県の情報を見て変更がないか確認しておいた方が良いですよ。
新課程に向けて入試に求める内容が変更されている都道府県もあります。