秋田県公立高校入試(2019年度)の数学第5問(選択問題)の解説

秋田県で2019年（平成31年度)に行われた公立高校入試の数学第5問(学校選択)の問題と解説です。
どちらも動点問題ですが、立方体の辺上を1点が動く問題と正八面体の辺上を2点が動く違いがあります。
それほど難しい問題ではありませんが動点問題に共通のポイントがありますので確認しておきましょう。

問題は秋田県で公開してくれています。

⇒　2019年(平成31年)度秋田県公立高校入試数学問題

立方体の辺上を1点が動く問題

\(\,　\large{5}　\,\)は「指示された問題」について解答します。
問題の選択を間違えたら共通問題はないので\(\,0\,\)点ですよ。

\(\,\large{Ⅰ}\,\)
立方体の\(\,1\,\)辺は\(\,10\,\)で、点Mは\(\,\mathrm{GH}\,\)の中点です。
（長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。）

点\(\,\mathrm{P}\,\)は毎秒\(\,1\,\)の速さで
　\(\,\mathrm{A\,→\,B\,→\,F\,→\,G}\,\)
の順に動きます。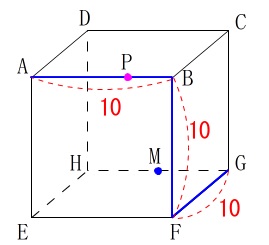点\(\,\mathrm{P}\,\)は\(\,x\,\)秒で\(\,x\,(\mathrm{cm})\,\,\)動きます。

このとき、\(\,\mathrm{△AFP}\,\)の面積を\(\,y\,\)とします。

動点問題のポイントは変化が起こる点で場合を分けて見る、ということです。
この問題では\(\,\mathrm{B,F}\,\)で変化が起こるので、
点\(\,\mathrm{P}\,\)が、　
　\(\,0≦x≦10\,\)　\(\,\mathrm{AB}\,\)間
　\(\,10≦x≦20\,\)　\(\,\mathrm{BF}\,\)間
　\(\,20≦x≦30\,\)　\(\,\mathrm{FG}\,\)間
にいるときを別々に見ておけば良いのです。

(1)
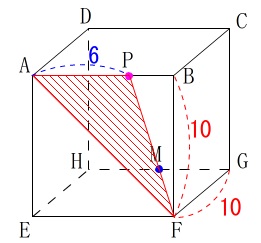
\(\,x=6\,\)のときは点\(\,\mathrm{P}\,\)は\(\,\mathrm{AB}\,\)間にいます。
\(\,x\,\)の関数で表すこともできますが、具体的に求めておきます。

\(\,\mathrm{△AFP}\,\)の面積\(\,y\,\)は線分\(\,\mathrm{AP}\,\)を底辺、\(\,\mathrm{BF}\,\)を高さとする三角形の面積だから
　\(\,\mathrm{AP=\color{blue}{6}}\,\)
　\(\,\mathrm{BF=\color{red}{10}}\,\)
なので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \color{blue}{6}\times \color{red}{10}\\
&=&\underline{　30　}
\end{eqnarray}\)

(2)
\(\,10≦x≦20\,\)のとき点\(\,\mathrm{P}\,\)は\(\,\mathrm{BF}\,\)上にいます。
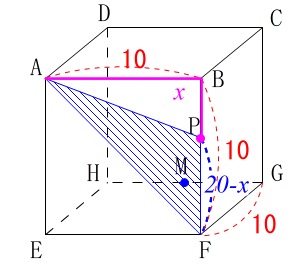このとき点\(\,\mathrm{P}\,\)は\(\,x\,\)秒間で\(\,\mathrm{\color{magenta}{AB+BP}}\,\)だけ動いています。

つまり、
　\(\,\mathrm{AB+BP}=x\,\)
なので\(\,\mathrm{PF}\,\)は正方形の辺\(\,2\,\)つ分から動いた\(\,x\,\)を引いた長さで、
\(\,\mathrm{AB+BF}=20\,\)だから
　\(\,\mathrm{PF}=\color{blue}{20-x}\,\)

\(\,\mathrm{△APF}\,\)の面積\(\,y\,\)は底辺が\(\,\mathrm{PF}\,\)、高さが\(\,\mathrm{AB}\,\)と見ることができるので、
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \mathrm{PF}\times \mathrm{AB}\\
&=&\frac{1}{2}\times (20-x)\times 10\\
&=&5(20-x)
\end{eqnarray}\)

これが\(\,y=24\,\)となるのは

　\(\begin{eqnarray}\displaystyle
5(20-x)&=&24\\
100-5x&=&24\\
-5x&=&-76\\
x&=&\underline{　\frac{76}{5}　}
\end{eqnarray}\)

これは\(\,10≦x≦20\,\)にあるので適しています。

動点問題ではこの動いた\(\,\mathrm{P}\,\)の長さをどう利用するかがポイントです。
もちろん、変化する区間を分けることもですよ。

(3)
折れた線分が最も短くなるのは、直線になるときです。

\(\,\mathrm{BP}\,\)や\(\,\mathrm{PM}\,\)は立方体の表面上の線分なので折れ曲がっていて空間のような感じがするかもしれませんが、
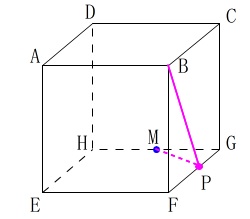展開図の上では単なる折れ線です。
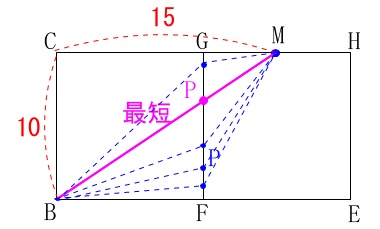点\(\,\mathrm{B}\,\)と点\(\,\mathrm{M}\,\)は定点なので、
　\(\,\mathrm{BC}=\color{red}{10}\,,\,\mathrm{CM}=\color{red}{15}\,\)
は変わりません。

点\(\,\mathrm{P}\,\)が\(\,\mathrm{FG}\,\)上を動くとき線分\(\,\mathrm{BP,PM}\,\)の長さの和が最も短くなるのは、

　\(\,\mathrm{B\,,\,P\,,\,M}\,\)が一直線になるとき

なので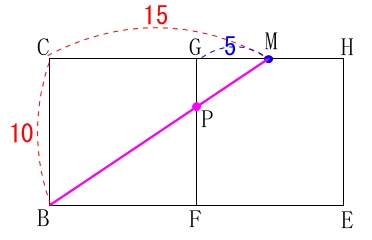\(\,\mathrm{△MGP}\,\)　∽　\(\,\mathrm{△MCB}\,\)
だから
　\(\begin{eqnarray}
\mathrm{MG:MC}&=&\mathrm{GP:CB}\\
\color{blue}{5}:\color{red}{15}&=&\mathrm{\color{blue}{GP}}:\color{red}{10}\\
15\,\mathrm{\color{blue}{GP}}&=&10\times 5\\
\mathrm{GP}&=&\frac{10\times 5}{15}\\
&=&\color{blue}{\frac{10}{3}}
\end{eqnarray}\)

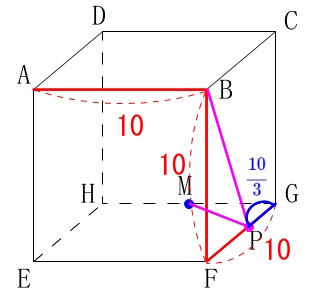
点\(\,\mathrm{P}\,\)が\(\,\mathrm{G}\,\)まで動いたとき\(\,30\,\)で、
残りが\(\,\mathrm{GP}\,\)だから
　\(\begin{eqnarray}\displaystyle
x&=&30-\color{blue}{\frac{10}{3}}\\
&=&\underline{　\frac{80}{3}　}
\end{eqnarray}\)

このとき\(\,\mathrm{PF}\,\)と面\(\,\mathrm{ABFE}\,\)そのものが垂直なので、
\(\,\mathrm{PF\,⊥\,AF}\,\)となるので\(\,\mathrm{△APF}\,\)は直角三角形です。

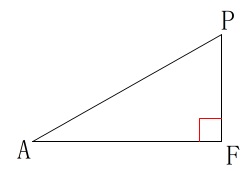
　\(\begin{eqnarray}
\mathrm{PF}&=&\mathrm{GF-GP}\\
&=&10-\frac{10}{3}\\
&=&\color{red}{\frac{20}{3}}
\end{eqnarray}\)

であり、正方形の対角線であることから

　\(\begin{eqnarray}
\mathrm{AF^2}&=&10^2+10^2\\
&=&200\\
\mathrm{AF}&=&\color{magenta}{10\sqrt{2}}　(\,\mathrm{AF}\,＞\,0\,)
\end{eqnarray}\)

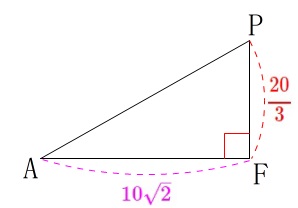
よって求める\(\,\mathrm{△AFP}\,\)の面積\(\,y\,\)の値は

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \mathrm{AF}\times \mathrm{P}F\\
&=&\frac{1}{2}\times \color{magenta}{10\sqrt{2}}\times \color{red}{\frac{20}{3}}\\
&=&\underline{　\frac{100\sqrt{2}}{3}　}
\end{eqnarray}\)

ここまで理解しておけば選択問題\(\,\large{Ⅱ}\,\)は形は違いますが似たような問題になります。

正八面体の辺上を2点が動く問題

　\(\,\mathrm{　\large{Ⅱ}　}\,\)

こちらの問題を選択する時点で教科書の基本的なことは覚えている、
ということで簡単に説明します。

わかりにくい場合は\(\,\mathrm{\large{　Ⅰ　}}\,\)にあるポイントに目を通すと少しは分かり易くなります。

正八面体があって、点\(\,\mathrm{M}\,\)は\(\,\mathrm{BC}\,\)の中点です。
\(\,2\,\)点\(\,\mathrm{P,Q}\,\)が点\(\,\mathrm{A}\,\)を同時に出発し、
　点\(\,\mathrm{P}\,\)は毎秒\(\,1\,\)の速さで
　\(\,\mathrm{\color{red}{A\,→\,B\,→\,F}}\,\)
　点\(\,\mathrm{Q}\,\)は毎秒\(\,2\,\)の速さで
　\(\,\mathrm{\color{blue}{A\,→\,C\,→\,D\,→\,A\,→\,B}}\,\)
の順に動きます。（単位は\(\,\mathrm{cm}\,\)ですが省略しています。）
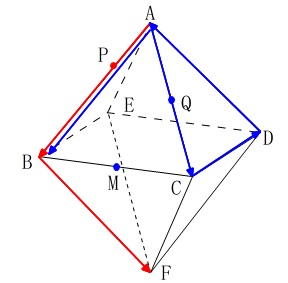点\(\,\mathrm{P,Q}\,\)が点\(\,\mathrm{A}\,\)を出発してから\(\,x\,\)秒後の\(\,\mathrm{△APQ}\,\)の面積が\(\,y\,\)です。

(1)
\(\,x=4\,\)のとき、点\(\,\mathrm{P}\,\)は\(\,\mathrm{AB}\,\)上に、点\(\,\mathrm{Q}\,\)は\(\,\mathrm{AC}\,\)上にあります。

\(\,\mathrm{△ABC}\,\)は正三角形なので\(\,\mathrm{∠BAC=60^{\circ}}\,\)で、
\(\,\mathrm{AP=4\,,\,AQ=8}\,\)の三角定規の状態です。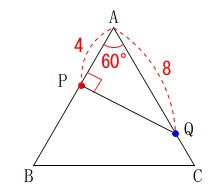このとき、
　\(\mathrm{PQ}=4\sqrt{3}\)

よって\(\,x=4\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \mathrm{AP}\times \mathrm{PQ}\\
&=&\frac{1}{2}\times 4\times 4\sqrt{3}\\
&=&\underline{　8\sqrt{3}　}
\end{eqnarray}\)

(2)
\(\,10\,≦\,x\,≦\,15\,\)のとき、
点\(\,\mathrm{P}\,\)は\(\,\mathrm{BF}\,\)上に、点\(\,\mathrm{Q}\,\)は\(\,\mathrm{DA}\,\)上にあります。

四角形\(\,\mathrm{ABFD}\,\)は正方形なので\(\,\mathrm{△APQ}\,\)の高さは正方形の\(\,1\,\)辺と同じ\(\,\color{blue}{10}\,\)です。
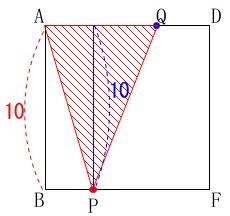点\(\,\mathrm{Q}\,\)は\(\,\mathrm{A→C→D}\,\)と動いたときに\(\,30\,\)なので、\(\,x\,\)秒後の\(\,\mathrm{AQ}\,\)の長さは
　\(\mathrm{AQ}=30-x\)
となるので、
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (30-x)\times 10\\
&=&\color{red}{5(30-x)}
\end{eqnarray}\)

\(\,y=\color{blue}{24}\,\)となるとき

　\(\begin{eqnarray}
\color{blue}{24}&=&\color{red}{5(30-2x)}\\
24&=&150-10x\\
10x&=&126\\
x&=&\frac{126}{10}\\
&=&\underline{　\frac{63}{5}　}
\end{eqnarray}\)

これは\(\,10\,≦\,x\,≦\,15\,\)に適しています。

(3)
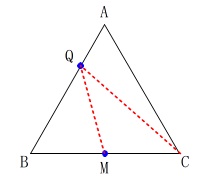
\(\,15\,≦\,x\,≦\,20\,\)のとき、
点\(\,\mathrm{P}\,\)は\(\,\mathrm{BF}\,\)上にあり、点\(\,\mathrm{Q}\,\)は\(\,\mathrm{AB}\,\)上にあります。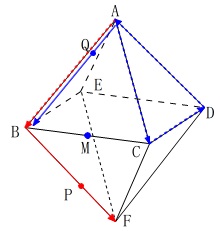線分\(\,\mathrm{CQ}\,\)と線分\(\,\mathrm{QM}\,\)の長さの和が最も短くなるとき、
つまり、\(\,\mathrm{CQ+QM}\,\)が最小になるのは、
　\(\,\mathrm{C,Q,M}\,\)が折れ線ではなく直線
になるときです。
しかし、実際には直線に並ぶことはないので、ひとつ正三角形を付け足します。
\(\,\mathrm{AB}\,\)を軸として\(\,\mathrm{△ABC}\,\)を対称します。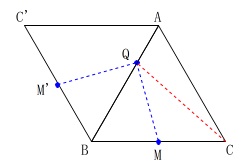
合同な図形を書き足しただけだから\(\,\mathrm{QM}\,\)と\(\,\mathrm{QM’}\,\)は同じ長さなので、
　\(\,\mathrm{C,Q,M’}\,\)が直線になるとき
を考えます。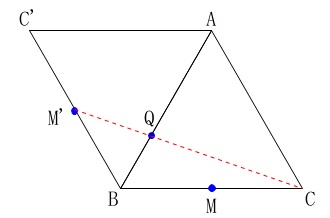点\(\,\mathrm{Q}\,\)が\(\,\mathrm{B}\,\)まで移動したとき\(\,40\,\mathrm{cm}\,\)なので、
動点\(\,\mathrm{Q}\,\)の速さが\(\,2\,\)なので\(\,x\,\)秒後は
　\(\,\mathrm{BQ}=\color{red}{40-2x}\,\)
このとき、
　\(\begin{eqnarray}
\mathrm{AQ}&=&10-(40-2x)\\
&=&\color{blue}{2x-30}\end{eqnarray}\)
また、
　\(\,\mathrm{BM’=BM=\color{red}{5}}\,\)
　\(\,\mathrm{AC=\color{blue}{10}}\,\)
は、正三角形の\(\,1\,\)辺が\(\,10\,\)であることから分かっています。
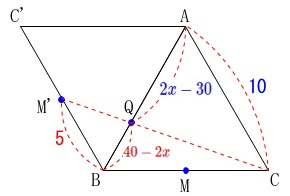\(\,\mathrm{△QAC}\,\)　∽　\(\,\mathrm{△QBM’}\,\)なので

　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{QA}:\color{red}{QB}}&=&\mathrm{\color{blue}{AC}:\color{red}{BM’}}\\
(\color{blue}{2x-30}):(\color{red}{40-2x})&=&\color{blue}{10}:\color{red}{5}\\
10(40-2x)&=&5(2x-30)\\
400-20x&=&10x-150\\
-30x&=&-550\\
x&=&\frac{550}{30}\\
&=&\underline{　\frac{55}{3}　}
\end{eqnarray}\)
点\(\,\mathrm{P}\,\)と点\(\,\mathrm{Q}\,\)は、正方形\(\,\mathrm{ABFD}\,\)上にあります。
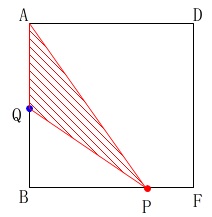\(\,\mathrm{△APQ}\,\)の底辺は\(\,\mathrm{AQ}\,\)と見ることができ、

　\(\begin{eqnarray}\displaystyle
\mathrm{AQ}&=&2x-30\\
&=&2\times \frac{55}{3}-30\\
&=&\color{red}{\frac{20}{3}}
\end{eqnarray}\)

また点\(\,\mathrm{P}\,\)は毎秒\(\,1\,\)の速さなので\(\,x\,\)秒動いたとき、
\(\,\mathrm{AB}\,\)間の\(\,10\,\)を引いて

　\(\begin{eqnarray}\displaystyle
\mathrm{BP}&=&x-10\\
&=&\frac{55}{3}-10\\
&=&\color{blue}{\frac{25}{3}}
\end{eqnarray}\)

これが\(\,\mathrm{△APQ}\,\)の高さになります。
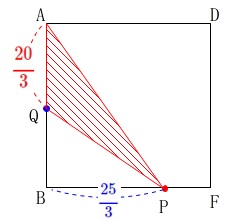よって、\(\,\mathrm{△APQ}\,\)の面積\(\,y\,\)は、

　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times \mathrm{AQ}\times \mathrm{BP}\\
&=&\frac{1}{2}\times \color{red}{\frac{20}{3}}\times \color{blue}{\frac{25}{3}}\\
&=&\underline{　\frac{250}{9}　}
\end{eqnarray}\)

\(\,2019\,\)年度の秋田県公立入試の数学問題はここまでです。

⇒　秋田県公立高校入試2020年(令和2年)度の数学の問題と解説

\(\,2020\,\)年度も学校別の問題がありますので確認しておきましょう。

⇒　秋田県公立高校入試2018数学の過去問と解説

似たような傾向ですので\(\,2018\,\)年度と見比べてみて下さい。
この先、新課程に向けて少しは変わるかもしれませんが基本中心であることは変わらないでしょう。

⇒　2019年(平成31年)度秋田県公立高校入試の数学の問題と解説

もう一度第\(\,1\,\)問から通して見て、基本中心であることを確認して下さい。